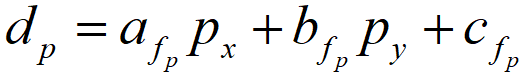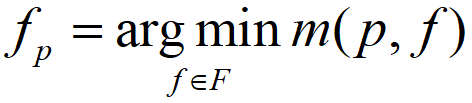【理论恒叨】【立体匹配系列】经典PatchMatch: （1）Slanted support windows倾斜支持窗模型

一枝独秀不是春

理论恒叨系列

【理论恒叨】【立体匹配系列】经典PatchMatch: （1）Slanted support windows倾斜支持窗模型
【理论恒叨】【立体匹配系列】经典PatchMatch: （2）基于PatchMatch的视差估计
【理论恒叨】【立体匹配系列】经典PatchMatch: （3）后处理（一致性检查与视差填充）

PatchMatchStereo¹是Michael Bleyer等在2011年发表于British Machine Vision Conference（BMVC）上的一篇双目立体匹配算法文章，非常经典，倾斜支持窗的思路打破传统固定窗口式局部匹配的思维桎梏，在Middlebury数据集上获得非常好的匹配效果，一段时间内高居排行榜第一名。更难能可贵的是，它和SGM一样数据泛化能力出色，对大部分数据都能取得不错的结果，所以也被很多商业软件所实现，是真正能够产品化的算法。

本系列博主将为大家介绍经典的PatchMatchStereo算法原理，希望能够对同学们的立体匹配算法研究有所帮助。

本篇的内容是算法的核心模型：倾斜支持窗模型Slanted support windows。

倾斜支持窗Slanted support windows

在介绍倾斜支持窗（Slanted support windows）之前，非常有必要介绍下另一种窗模型：Fronto-parallel windows。

Fronto-parallel windows

Fronto-parallel windows是非常经典的窗口模型，它的含义是立体相机正前方与极线纠正后的像平面平行的窗口，同时也和纠正后每个相机的相机坐标系Z轴垂直。该窗口的特性是：

• 窗口内的任意线段在左右图像（核线像对）上的投影长度相等。
• 窗口内的所有空间点的深度一样，由$D=bf/d$可知空间点在影像上的投影点视差也相同。

这两个特性对矩形窗口匹配来说是非常友好的，使得左右图像以某同名点对为中心的窗口内的所有像素都能一一同名对应，窗口内所有像素存在相同的唯一视差，这样如果纹理条件上佳，则不需要代价聚合，只通过相关系数法等局部相似度算法就能得到不错的结果。

但问题在于，这样的窗口太理想化了，你很难在实际应用中找到这样的场景，更多情况是：场景内可能存在若干个Fronto-parallel windows，也可能一个也没有。但庆幸的是，该窗口为我们提供了很好的研究思路，很多算法都是基于此窗口模型而进一步优化，如SGM、AD-Census，它们基于Fronto-parallel windows计算初始代价值，然后经过代价聚合，对代价进行优化，得到很不错的效果。

另一部分学者则开始另辟蹊径，寻找其他更合理的窗口模型。而且他们做到了，2011年，基于Slanted support windows的PatchMatchStereo¹立体匹配算法应运而生。

Slanted support windows

我们先来看一张图：

图中，绿色的线条表示表面的一维表示，红色线段是窗口的一维表示，左边是Fronto-parallel windows示意图，可以看到P是符合Fronto-parallel windows假设的，局部表面是Fronto-parallel的，同一个视差值；而R和S不符合，表面都是倾斜，R是倾斜平面而S是倾斜曲面。右边是Slanted support windows示意图，我们可以观察R和S窗口的变化，Fronto-parallel windows假设下的窗口是和视差维平行的，并不贴合表面走势，而Slanted support windows是很好的贴合表面的。从图中我们可以看出来，Slanted support windows应该是随着表面的朝向而动态变化的，具体是如何变化，下面我会介绍。

另一个区别是，Fronto-parallel windows基于整像素视差，而Slanted support windows基于子像素视差。如Q点，局部表面的视差值不是整数值，如果是Fronto-parallel windows模型，只能匹配整像素视差（Fronto-parallel windows一般采用一元二次拟合来得到子像素精度），而Slanted support windows直接使用子像素位置的窗口，可以更好的贴合Q处的表面。

好了，大概对Slanted support windows有了个初步的印象，但大家估计还是一知半解，所以Slanted support windows模型到底具体是怎么实现的？听博主慢慢介绍。

Slanted support windows模型

上一节，我们猜想到PMS的Slanted support windows应该是随着表面的朝向而动态变化的，而且图中还可以看到Slanted support windows是一个平面窗口而并不是曲面窗口，PMS的出发点是为所有像素点都找到一个属于它的动态的视差平面，设像素点$p$的视差为$d_p$，则$p$的视差平面方程为

式中， $a_{f_p}$、$b_{f_p}$、$c_{f_p}$为视差平面的3个参数，$p_x$、$p_y$为像素的$xy$坐标值。如此又来视差估计问题转换为平面估计问题，立体匹配就是要找出每个像素的最优平面的参数，也就是对每个像素找出聚合代价最小的那个平面：

式中$F$为一个无边界的平面集合，$m(p,f)$为像素$p$当视差平面为$f$时的聚合代价值，计算公式为：

式中，$W_p$是一个以$p$为中心的方形窗口，PMS也应用于时序立体，彼时$W_p$将是一个3D窗口，第3维是连续视频序列帧中的前后帧对应位置像素，这听起来一下子就高端新颖上档次了啊。

$w(p,q)$是自适应的权值，为了解决edge-fattening问题，edge-fattening做立体匹配的同学一定遇到过：有视差非连续现象出现的边缘位置总是会有一圈连续的错误匹配值，它不是离群误差，而是让边缘扩大了一圈，通过一致性检查等手段都难以剔除。一个典型的例子是匹配张开的手掌，视差图会让手掌在根部粘连起来，如下图右列就是典型的edge-fattening问题。

PMS计算$w(p,q)$的方法是计算$p$和$q$为同一个平面的可能性，通过颜色的差异来判断，公式如下：

式中，$\gamma$为自定义参数$，||I_p-I_q||$为像素$p$和$q$在RGB空间的L1-distance（就是$|r-r|+|g-g|+|b-b|$）。相邻像素颜色差异越大，为同一平面的可能性越小，则$w(p,q)$越小，合理！

我们再来看最关键的$\rho$。它是在衡量两个像素的不相似性。假设左视图像素$q$的视差平面方程为($a_f$,$b_f$,$c_f$)，则它的视差值$d_q=a_f{q}_x+b_f{q}_y+c_f$，在右视图上对应的同名点$q^{\prime }=q-d_q$，$q$和$q^{\prime }$的不相似性计算公式为：

式中$||▽I_p-▽I_{q^{\prime }}||$为$q$和$q^{\prime }$的梯度之差的绝对值，该式的含义就是两个像素的颜色相差越大、梯度相差越大，则不相似的程度越大，$\alpha$参数为自定义参数，在颜色和梯度之间做一个平衡。注意到根据平面算出来的视差值是小数值，所以像素$q^{\prime }$的位置不是整数而是小数，它的颜色值和梯度值通过线性内插得到。

参数${\tau }_{col}$和${\tau }_{grad}$为自定义截断参数，为了让遮挡区的像素代价计算更鲁棒，意思就是不能让代价过大，保持在一个良好的局部范围内。

以上，我们便了解如何计算像素$p$在视差平面为$f_p$时的聚合代价$m(p,f)$，从而可以判定$f_p$的孰好孰坏而做出最优的选择（选择代价最小的$f_p$自不必说）。

自然不能在一个无边界平面集$F$里用暴力穷举法搜索最小值。如何搜索，是PMS另一个及其出彩且与众不同的地方，同学们请听下回分解。

哈哈，放一张图吊下胃口：

博主简介：
Ethan Li 李迎松
武汉大学 摄影测量与遥感专业博士

主方向立体匹配、三维重建

2019年获测绘科技进步一等奖（省部级）

爱三维，爱分享，爱开源
GitHub： https://github.com/ethan-li-coding
邮箱：[email protected]

个人微信：

欢迎交流！

喜欢博主的文章不妨关注一下博主的博客，感谢！
博客主页：https://blog.csdn.net/rs_lys

---

1. Bleyer M , Rhemann C , Rother C . PatchMatch Stereo - Stereo Matching with Slanted Support Windows[C]// British Machine Vision Conference 2011. ↩︎ ↩︎