最基本的蚁群算法优化(ACO)算法——蚂蚁系统(AS)(TSP问题)
一、实验项目: 蚁群算法优化
二、实验目的:
理解并掌握蚁群算法的基本原理、思想,能够实现基本的蚁群算法,并利用蚁群算法求解旅行商(TSP)问题
三、实验内容:
1、旅行商问题:一个商人去N个城市卖货,要求所有城市都只走一遍,再回到起点,使得所走的路线最短
2、编程实现蚁群算法,并验证算法的正确性
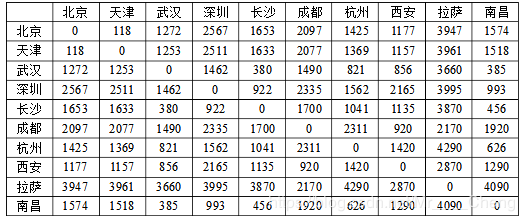
3、实验数据如下:一共有10个城市,单元格表示行标和列表之间的距离(单位km),例如118表示北京和天津的距离为118km
4、自定义相关参数,记录实验数据(迭代次数,每一代的最短路线长度)
代码:
import random
import math
import copy
import matplotlib.pyplot as plt
# 参数设置
max = 10000 # 设置一个最大距离,为了表示自己到自己不可达。
ant_num = 12 # 蚂蚁数目
alpha = 1 # 信息素因子
beta = 2 # 启发函数因子
rho = 0.5 # 信息挥发因子
city_num = 10 # 城市数量
best_ants_total_distance = [] # 记录每次迭代最优解 用于画图
# 城市距离矩阵
citys_distance = [[max,118,1272,2567,1653,2097,1425,1177,3947,1574],
[118,max,1253,2511,1633,2077,1369,1157,3961,1518],
[1272,1253,max,1462,380,1490,821,856,3660,385],
[2567,2511,1462,max,922,2335,1562,2165,3995,993],
[1653,1633,380,922,max,1700,1041,1135,3870,456],
[2097,2077,1490,2335,1700,max,2311,920,2170,1920],
[1425,1369,821,1562,1041,2311,max,1420,4290,626],
[1177,1157,856,2165,1135,920,1420,max,2870,1290],
[3947,3961,3660,3995,3870,2170,4290,2870,max,4090],
[1574,1518,385,993,456,1920,626,1290,4090,max]]
# 城市索引表
citys = ['北京','天津','武汉','深圳','长沙','成都','杭州','西安','拉萨','南昌']
# 贪婪算法求C_nn
def Greedy():
L = []
k = 0
L.append(k)
for i in range(city_num):
temp = max
m = k
for j in range(city_num):
if(((j) not in L) and citys_distance[m][j]<temp):
temp = citys_distance[m][j]
k=j
L.append(k)
C_nn = 0
for i in range(len(L)):
C_nn = C_nn + citys_distance[L[i]][L[(i+1)%10]]
return C_nn
class Ant():
# 初始化
def __init__(self,id):
self.ID = id
self.clean_data()
def clean_data(self):
self.path = []
self.total_distance = 0.0
self.move_times = 0
start = random.randint(0,city_num-1)
self.current_city = start
self.open_table_city = [True for i in range(city_num)]
self.path.append(self.current_city)
self.open_table_city[start] = False
self.move_times = 1
# 选择下一个城市
def choice_next_city(self):
next_city = -1
select_citys_prob = [0.0 for i in range(city_num)]
total_prob = 0.0
# 获取去下一个城市的概率
for i in range(city_num):
if self.open_table_city[i]:
select_citys_prob[i] = pow(pheromone[self.current_city][i],alpha) * pow(1.0/citys_distance[self.current_city][i],beta)
total_prob += select_citys_prob[i]
# 轮盘选择城市
if total_prob > 0.0:
# 产生一个随机概率: 0.0 ~ total_prob
temp_prob = random.uniform(0.0,total_prob)
for i in range(city_num):
if self.open_table_city[i]:
# 轮次相减
temp_prob -= select_citys_prob[i]
if temp_prob < 0.0:
next_city = i
break
if (next_city == -1):
next_city = random.randint(0,city_num-1)
while ((self.open_table_city[next_city]) == False):
next_city = random.randint(0,city_num-1)
return next_city
# 移动
def move(self,next_city):
self.path.append(next_city)
self.open_table_city[next_city] = False
self.total_distance += citys_distance[self.current_city][next_city]
self.current_city = next_city
self.move_times += 1
# 搜索路径
def search_path(self):
# 初始化数据
self.clean_data()
# 搜索路径,遍历所有城市
while self.move_times < city_num:
# 移动下一城市
next_city = self.choice_next_city()
self.move(next_city)
# 回路 计算总距离
last_distance = citys_distance[self.path[-1]][self.path[0]]
self.total_distance += last_distance
class TSP():
# 初始化
def __init__(self,n):
self.runnum = n # 初始迭代次数
self.ants = [Ant(ID) for ID in range(ant_num)] # 初始蚁群
self.best_ant = Ant(-1) # 初始最优解
self.best_ant.total_distance = 1000000 # 初始最大距离
def search_path(self):
for i in range(self.runnum):
# 遍历每一只蚂蚁
for ant in self.ants:
# 搜索一条路径
ant.search_path()
# 与当前最优蚂蚁比较
if ant.total_distance < self.best_ant.total_distance:
# 更新最优解
self.best_ant = copy.deepcopy(ant)
# 更新信息素
self.update_pheromone()
best_ants_total_distance.append(self.best_ant.total_distance)
# break
# if(i%10 == 0):
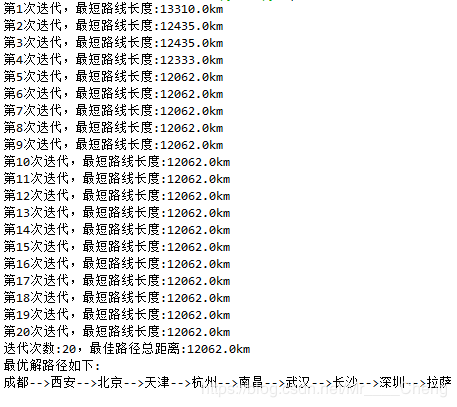
print("第{0}次迭代,最短路线长度:{1}km".format(i+1,self.best_ant.total_distance))
print("迭代次数:{0},最佳路径总距离:{1}km".format(i+1,self.best_ant.total_distance))
print("最优解路径如下:")
for i in range(city_num):
if(i==city_num-1):
print(citys[self.best_ant.path[i]])
else:
print("{0}-->".format(citys[self.best_ant.path[i]]),end='')
# 更新信息素
def update_pheromone(self):
# 获取每只蚂蚁在其路径上留下的信息素
temp_pheromone = [[0.0 for col in range(city_num)] for raw in range(city_num)]
for ant in self.ants:
for i in range(1,city_num):
start,end = ant.path[i-1] ,ant.path[i]
# 在路径上的每两个相邻城市捡留下的信息素,与路径总距离成反比
temp_pheromone[start][end] += 1 / ant.total_distance
temp_pheromone[end][start] = temp_pheromone[start][end]
# 更新所有城市之间的信息素,就的信息素衰减加上新迭代信息素
for i in range(city_num):
for j in range(city_num):
pheromone[i][j] = pheromone[i][j] * rho + temp_pheromone[i][j]
if __name__ == "__main__":
global pheromone
C_nn = Greedy()
pheromone = [[ant_num/C_nn for col in range(city_num)] for raw in range(city_num)]
TSP(20).search_path()
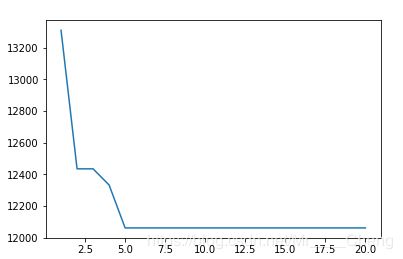
# 画图
X = [x for x in range(1,21)]
Y = best_ants_total_distance
plt.plot(X,Y)
plt.show()