HW02 lambda函数的一个问题

阐述一个有关lambda函数的问题

首先定义accumulate函数

def accumulate(combiner, base, n, term):
    """Return the result of combining the first n terms in a sequence and base.
    The terms to be combined are term(1), term(2), ..., term(n).  combiner is a
    two-argument commutative, associative function.

    >>> accumulate(add, 0, 5, identity)  # 0 + 1 + 2 + 3 + 4 + 5
    15
    >>> accumulate(add, 11, 5, identity) # 11 + 1 + 2 + 3 + 4 + 5
    26
    >>> accumulate(add, 11, 0, identity) # 11
    11
    >>> accumulate(add, 11, 3, square)   # 11 + 1^2 + 2^2 + 3^2
    25
    >>> accumulate(mul, 2, 3, square)    # 2 * 1^2 * 2^2 * 3^2
    72
    >>> accumulate(lambda x, y: x + y + 1, 2, 3, square)
    19      #(((2 + 1^2 + 1) + 2^2 + 1) + 3^2 + 1)
    """
    i=1
    while i<=n:
        base=combiner(base,term(i))
        i+=1
    return base

Make Repeater问题

Implement a function make_repeater so that make_repeater(f, n)(x) returns f(f(…f(x)…)), where f is applied n times. That is, make_repeater(f, n) returns another function that can then be applied to another argument. For example, make_repeater(square, 3)(42) evaluates to square(square(square(42))). See if you can figure out a reasonable function to return for that case. You may use either loops or recursion in your implementation.

def make_repeater(f, n):
    """Return the function that computes the nth application of f.

    >>> add_three = make_repeater(increment, 3)
    >>> add_three(5)
    8
    >>> make_repeater(triple, 5)(1) # 3 * 3 * 3 * 3 * 3 * 1
    243
    >>> make_repeater(square, 2)(5) # square(square(5))
    625
    >>> make_repeater(square, 4)(5) # square(square(square(square(5))))
    152587890625
    >>> make_repeater(square, 0)(5) # Yes, it makes sense to apply the function zero times! 
    5
    """
    "*** YOUR CODE HERE ***"
    
def compose1(f, g):
    """Return a function h, such that h(x) = f(g(x))."""
    def h(x):
        return f(g(x))
    return h

我的解答：

    if n==0:
        return identity
    g=f
    while n>1:
        f=compose1(f,g)
        n-=1
    return f

很自然的想法，用循环解决

补充问题：For an extra challenge, try defining make_repeater using compose1 and your accumulate function in a single one-line return statement.

答案：

def make_repeater2(f, n):
    return accumulate(compose1, lambda x: x, n, lambda i: f)

对应表格：

combiner	compose1
base	lambda x: x
n	n
term	lambda i: f

这里的重点是lambda i: f 这个隐式函数，lambda x: 2*x 表示输入参数x，输出2x，lambda i: f就表示输入参数i=1，2，3，4…恒输出f

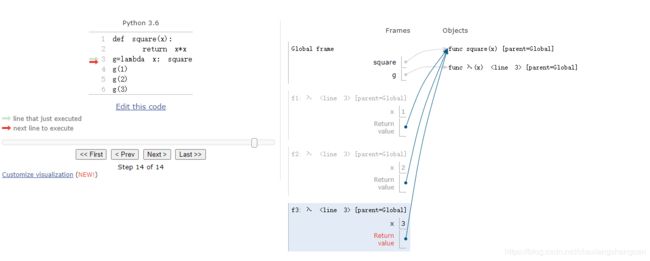
这里可以看到 g=lambda x: square, g(1),g(2),g(3) 都是square函数。由此可见lambda函数在high-older function中有简化结构的作用，给人的感觉比较微妙，可参考curry（柯里化）的知识