ROS麦克纳姆轮底盘制作(上)
目录
1.底盘硬件框图
2、麦克纳姆轮模型介绍
2.1逆解运动学模型
2.2正解运动学模型
3 底盘软件框架
4 参考资料
在这一个专题中,我们将介绍如何搭建利用麦克纳姆轮搭建一个ROS底盘。参考标准的ROS底盘,ROS底盘应该具备接收导航节点发送的“cmd_vel”这个话题上的控制命令(小车X,Y,Z三个方向的速度以及三个方向的角速度),同时更加底盘轮子的转速信息预估底盘的位置,并发布到Odometry(里程计)话题上。
整个专题分为了四个部分实现:
1、首先介绍小车的硬件结构,
2、其次介绍麦克纳姆轮的运动学模型,
3、接下来利用遥控器控制麦克纳姆轮前后左右移动实现遥控,
4、最后编写ROS节点将“cmd_vel”话题的数据转到底盘上。
所有的代码均放在了Github中,欢迎大家下载留言。
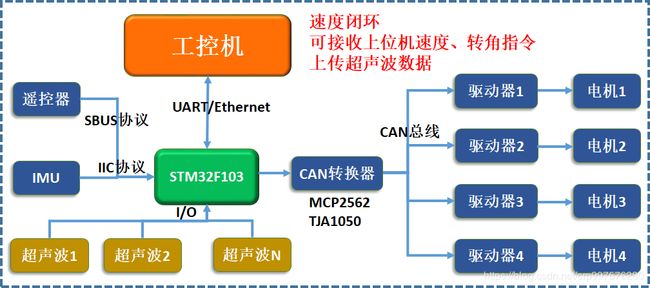
1.底盘硬件框图
底盘的主要任务是接收上位机的指令(即ROS节点的指令),控制每个电机的转速、同时上传底盘上的IMU、超声波、电机转速等传感器和执行器的信息到ROS中的底盘节点。这里我们涉及到传感器和执行器分别有:2.4G遥控器接收机、IMU、超声波传感器、4路大疆M3508电机及驱动器。其中遥控器用于辅助遥控底盘和切换控制方式、超声波用于弥补激光雷达的盲区,IMU用于测量底盘的姿态和航向角(在有些底盘中还使用了IMU的信息来做了转角控制的闭环)
图1-1 小车硬件框图
小车硬件实物如下图所示,定义左上角电机的编号为#1,左下为#2,右下为#3,右上为#4。正前方为X方向,水平方向为Y方向(与ROS中的坐标系相同)。
图1-2 小车硬件实物
底盘的开发任务分四步实现:
第一步,打通通讯链路,读取传感器(DBUS接收、IMU数据读取、超声波数据读取)和电机驱动器(C620)数据。
第二步:利用PI控制器实现电机的速度闭环控制。
第三步:利用麦克纳姆轮速度逆解模型实现X/Y/W三个方向的速度控制。
第四步:完善上位机收发指令协议、上传IMU、超声波、电机转速信息。
接下来我们先介绍一下麦克纳姆轮的运动学模型,这个运动学模型的主要是方便我们在X,Y,W三个方向的速度和四个电机的转速(V1,V2,V3,V4)之间建立映射关系。控制的时候导航模块给定的是X,Y方向的速度(m/s)以及小车的旋转速度W(rad/s),在发布里程计的时候,我们需要读取四个电机的转速或者转动的圈数来推算出小车的位置坐标和航向角。
2、麦克纳姆轮模型介绍
首先我们先从宏观的角度来分析一下麦克纳姆轮底盘是如何实现前后、左右、旋转运动的。
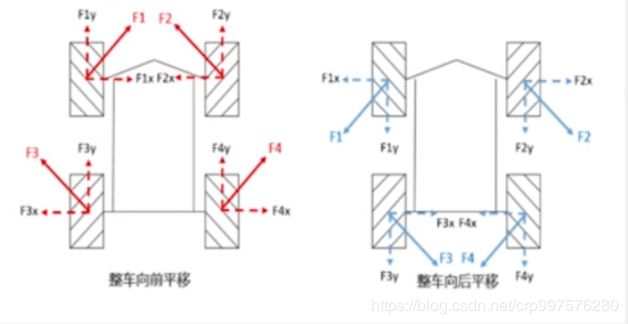
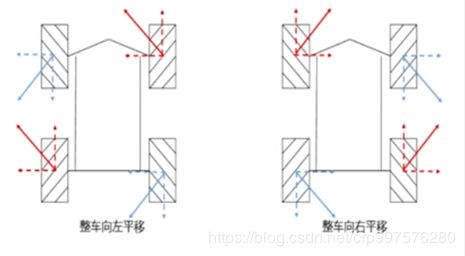
a. 前后运动 b. 左右运动

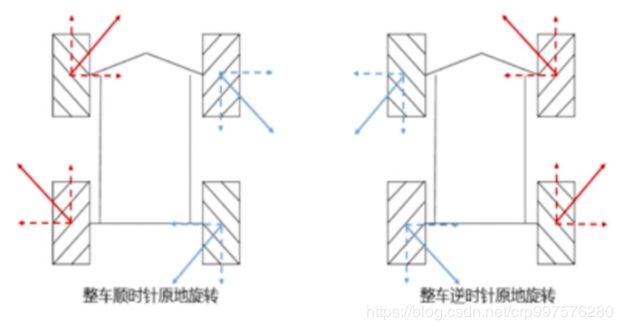
c. 45度斜向运动 d. 旋转运动
图2-1 麦克纳姆轮运动学模型示意图
麦克纳姆轮安装方式为“米”字形安装,如图1所示,假设我们需要控制小车动以下运动:
- 向前运动,那么需要四个轮子向前转动
- 向左运动时,需要左前和右后轮向后转动,左后和右前轮向前转动
- 向右前方运动时,左前和右前轮向前转动
- 逆时针旋转时,左前和左后向后转动,右前和右后向前转动
在参考[1]博客中已经给出了一个讲解麦克纳姆轮的经典教程,但是美中不足的是这个教程中的图片不知道怎么缘故无法显示,因此在参考这个大疆官网上的教程基础上进行了整理。
首先定义小车左右为Y方向,其中向左为正;前后为X方向,其中正前方为正;小车逆时针旋转为正用![]() 表示。假设小车速度为
表示。假设小车速度为![]() , 麦克纳姆轮从左上角到右上角标号依次为N=1,2,3,4。(Xn,Yn)为第n个轮相对原点的坐标,速度用
, 麦克纳姆轮从左上角到右上角标号依次为N=1,2,3,4。(Xn,Yn)为第n个轮相对原点的坐标,速度用![]() 表示。
表示。
各麦轮轮毂与X轴平行安装(通常呈米自形安装),r为轮毂半径,以逆时针方向偏转为正。![]() 为麦轮n的接地辊子轴线与X轴间的夹角【即辊子的偏置安装角,大小为45°】。辊子就是在麦克纳姆轮上斜着的那个。4个轮子的转速分别为
为麦轮n的接地辊子轴线与X轴间的夹角【即辊子的偏置安装角,大小为45°】。辊子就是在麦克纳姆轮上斜着的那个。4个轮子的转速分别为![]() 。定义好这些以后我们开始推导麦克纳姆轮的运动学模型。
。定义好这些以后我们开始推导麦克纳姆轮的运动学模型。
图2-2 小车硬件框图
2.1逆解运动学模型
已知四个轮子的转速![]() 求解车的速度
求解车的速度![]() ,也就是找到一个4x3矩阵R使得其满足:
,也就是找到一个4x3矩阵R使得其满足:
假设车身为刚体,每个麦轮的中心的水平和垂直速度分量![]() 均等于车的水平和垂直速度分量
均等于车的水平和垂直速度分量![]() 。此外,由于车身还有旋转速度
。此外,由于车身还有旋转速度![]() ,
, ![]() 也会在每个麦轮上产生的(水平和垂直方向)的速度分量
也会在每个麦轮上产生的(水平和垂直方向)的速度分量![]()
因此综合而言每个麦轮在水平和垂直方向的速度分量为:
(2.3)
到这我们求出了车身速度![]() 对应到每个麦轮上的速度
对应到每个麦轮上的速度![]() 的关系,接下来只要找到每个轮子转速
的关系,接下来只要找到每个轮子转速![]() 与
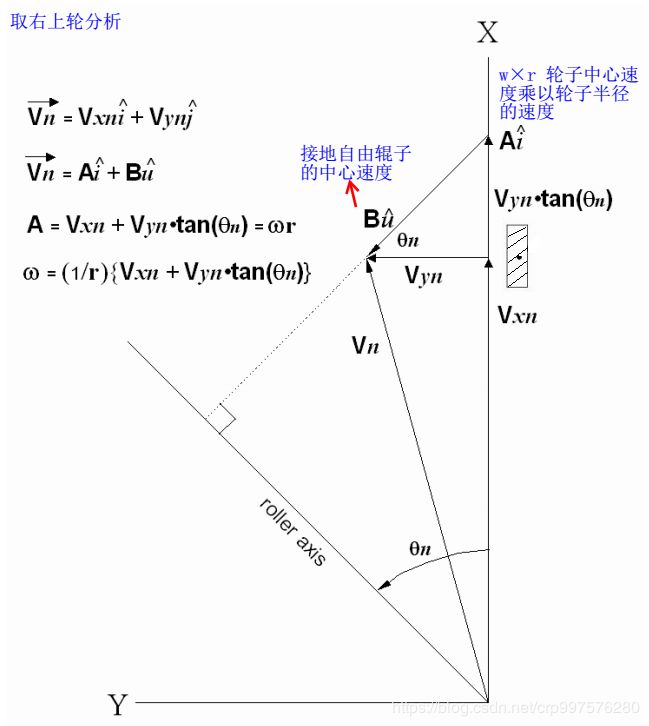
与![]() 之间的关系就构建完毕了。下图为右上轮在某一时刻的速度矢量关系。
之间的关系就构建完毕了。下图为右上轮在某一时刻的速度矢量关系。
图2-3 小车硬件框图
图2-3中Vn这个合速度矢量就是麦轮n当前的实际运动速度,由速度分量Vxn与Vyn合成。在图中还可以看出看出Vn是由麦轮n的轮毂中心速度Aî=ωn·r和接地自由辊子的中心速度Bû合成而来的(自由辊子的中心速度B是随速度矢量Vn变化的)。所以有等式:
![]() (2.4)
(2.4)
变形为:
(2.5)
对于4个轮子有:
(2.6)
根据第一图对θn的定义,可以得到θ1、θ3为 -45°,θ2、θ4为 +45°,因此R矩阵为:
(2.7)
通常我们设计的底盘是轴向对称的,也就是坐标系时原点到四个轮子的距离相等。所以每个轮横、纵坐标的绝对值各自相等,令K=abs(Xn)+abs(Yn),根据每个轮坐标所在象限的符号,矩阵可化简为:
另外,考虑î、û两个单位向量的线性组合,刚好构成XOY平面内的整个向量空间(当然实际上速度不可能无穷大的哈,但方向一定是全向的),这也就是麦轮能全向运动的原因。注意Bû始终是跟辊子轴垂直的,因为辊子一定是沿垂直其转轴的方向滚动,这就像Aî始终跟电机轴(平行于Y轴)垂直一样。
2.2正解运动学模型
正解运动学是指已知每个电机的转速,求出车体的速度。在数学形式上是找到一个3x4矩阵[F]使其满足:
![]() (2.9)
(2.9)
做法是通过最小二乘法来提供最优解的矩阵[F],首先从逆向运动学方程开始,
两边同时左乘[R]的转置得到:
两边同时左乘[R]’[R]的逆得到:
右侧化简为[V]得到:
![]() (2.13)
(2.13)
由此得到[F]:
![]() (2.14)
(2.14)
使用逆向运动学中化简完的[R]矩阵,很容易求出[F]:
注意:
公式2.1中速度![]() 的单位是m/s,而转速
的单位是m/s,而转速![]() 的单位为rad/s(弧度每秒),大疆C620电机编码器反馈的速度为rpm(转没分),这其中需要转换一下(
的单位为rad/s(弧度每秒),大疆C620电机编码器反馈的速度为rpm(转没分),这其中需要转换一下(![]() * 2*
* 2*![]() = rpm/60)
= rpm/60)
3 底盘软件框架
在上一章中,我们介绍了麦克纳姆轮底盘的基本框架,以及麦克纳姆轮运动学模型,这里我们通过大疆的遥控器以遥控的方式控制底盘实现前后左右运动。
底盘以STM32F1为核心,底盘可以分为以下几个功能模块:
- C620电调CAN驱动模块,通过CAN中断接收电机编码器反馈数据
- 接收DBUS协议的遥控器数据
- 设置速度PID闭环
- 上传4个电机的转角、转速、温度到上位机
具体而言首先使用串口1接收来至接收机的数据,然后由麦克纳姆轮运动学模型将X、Y、W三个方向上的速度转换为四个电机的目标转速(RPM)发送给PI控制作为目标速度,随后PI控制器接收四个轮子的目标转速实现速度闭环控制,并计算控制量,通过CAN总线传送到电机。最后由状态数据上传模块定时上传底盘上电机、IMU、超声波的数据到上位机上。
接线说明:
连线方面只需要把C620电调的CAN总线连上STM32、串口1接收引脚链接接收机(接收机与STM32之间需要外置一个反相器),串口2通过一条USB转串口的线连到上位机就可以了。
注:(大疆遥控器SW1需要拨到CL或者HL档位才有效,表示遥控器介入控制,OFF档表示撤销遥控器介入,由上位机进行控制)
代码就不贴出来了,感兴趣的小伙伴自行下载(底盘的代码)。到这里我们基本上可以实现用遥控器来遥控麦克纳姆轮底盘实现前、后、自旋三个方向的运动了。最后贴上一个效果图。
4 参考资料
[1]:大疆论坛,https://bbs.robomaster.com/thread-3960-1-1.html
[2]: 《Kinematic Analysis of Four-Wheel Mecanum Vehicle》
[3]: 代码地址:https://github.com/RuPingCen/mick_robot_chasiss
下一篇 : ROS底盘制作——麦克纳姆轮模型(下)
对于运行有问题的小伙伴欢迎邮件或留言讨论[email protected]


![{\rm{R = }}\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&{ - {\rm{K}}}\\ 1&1&{ - {\rm{K}}}\\ 1&{ - 1}&{\rm{K}}\\ 1&1&{\rm{K}} \end{array}} \right]](http://img.e-com-net.com/image/info8/32360141fabc4d3080c9e8347b61f455.gif)
