JZOJsenior5476.【NOIP2017提高组】day2T1奶酪

problem

Description

    现有一块大奶酪，它的高度为 h，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为z = 0，奶酪的上表面为z = h。
   现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。两相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。
   位于奶酪下表面的 Jerry 想知道，在 不破坏奶酪 的情况下，能否利用已有的空洞跑到奶酪的上表面去?

Input

 每个输入文件包含多组数据。
 输入文件的第一行，包含一个正整数 T，代表该输入文件中所含的数据组数。
 接下来是 T 组数据，每组数据的格式如下：
 第一行包含三个正整数 n，h 和 r，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。
 接下来的 n 行，每行包含三个整数 x、y、z，两个数之间以一个空格分开，表示空洞球心坐标为(x,y,z)。

Output

  输出文件包含 T 行，分别对应 T 组数据的答案，如果在第 i 组数据中，Jerry 能从下表面跑到上表面，则输出“ Yes ”，如果不能，则输出“ No ”（均不包含引号）。

Sample Input

3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4

Sample Output

Yes
No
Yes

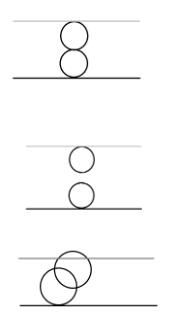
【输入输出样例 1 说明】
第一组数据，由奶酪的剖面图可见：
第一个空洞在（0，0，0）与下表面相切
第二个空洞在（0，0，4）与上表面相切
两个空洞在（0，0，2）相切
输出 Yes

第二组数据，由奶酪的剖面图可见：
两个空洞既不相交也不相切
输出 No

第三组数据，由奶酪的剖面图可见：
两个空洞相交
且与上下表面相切或相交
输出 Yes

Data Constraint

对于 20%的数据，n = 1，1 ≤ h , r ≤ 10,000，坐标的绝对值不超过 10,000。
对于 40%的数据，1 ≤ n ≤ 8， 1 ≤ h , r ≤ 10,000，坐标的绝对值不超过 10,000。
对于80%的数据，1 ≤ n ≤ 1,000， 1 ≤ h , r ≤ 10,000，坐标的绝对值不超过10,000。
对于 100%的数据，1 ≤ n ≤ 1,000，1 ≤ h , r ≤ 1,000,000,000，T ≤ 20，坐标的绝对值不超过 1,000,000,000。

---

analysis

day2T1比day1T1还™的水
对于每个数据，把最底层（或最上层）的点丢进队列里面，bfs既可
只要到达上层或下层直接输出Yes既可
（当然你也可以双向bfs但码量我不能保证，反正都能切掉）

注意了用c++的话会有蜜汁的范围太大的错误
当然啦pascal直接用精度媲美整数的extended恶心出题人既可

时间复杂度 O(Tn) 或 O(Tn12)
并查集什么的也是可以的啦！

---

code

单向bfs

const
        maxn=1000;
var
        a:array[0..maxn,0..3]of int64;
        bz:array[0..maxn]of boolean;
        queue:array[0..2*maxn]of longint;
        n,i,j,t,head,tail,now:longint;
        h,r:int64;
        bool:boolean;
function dis(x1,y1,z1,x2,y2,z2:extended):extended;
begin
        exit(sqrt(1.0*((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)+(z1-z2)*(z1-z2))))
end;
begin
        assign(input,'cheese.in');reset(input);
        assign(output,'cheese.out');rewrite(output);
        readln(t);
        while t>0 do
        begin
                dec(t);
                readln(n,h,r);
                fillchar(a,sizeof(a),0);
                fillchar(bz,sizeof(bz),true);
                fillchar(queue,sizeof(queue),0);
                head:=0;
                tail:=0;
                bool:=false;
                for i:=1 to n do
                begin
                        for j:=1 to 3 do read(a[i,j]);
                        readln;
                end;
                for i:=1 to n do
                begin
                        if a[i,3]-r<=0 then
                        begin
                                inc(tail);
                                queue[tail]:=i;
                                bz[i]:=false;
                        end;
                end;
                while headdo
                begin
                        inc(head);
                        now:=queue[head];
                        if a[now,3]+r>=h then
                        begin
                                bool:=true;
                                break;
                        end;
                        for i:=1 to n do
                        if (i<>now)and(bz[i])then
                        begin
                                if dis(a[now,1],a[now,2],a[now,3],a[i,1],a[i,2],a[i,3])<=2.0*r then
                                begin
                                        bz[i]:=false;
                                        inc(tail);
                                        queue[tail]:=i;
                                end;
                        end;
                end;
                if bool then writeln('Yes')
                else writeln('No');
        end;
        close(input);close(output);
end.