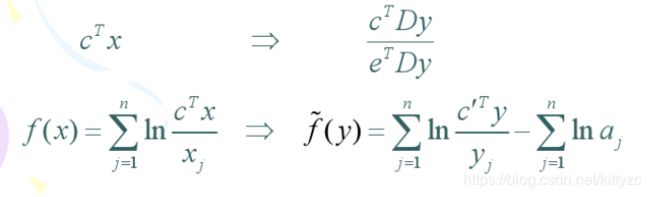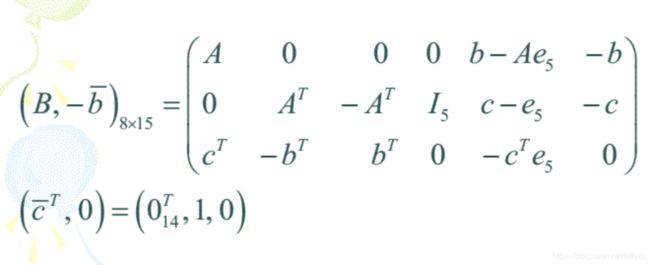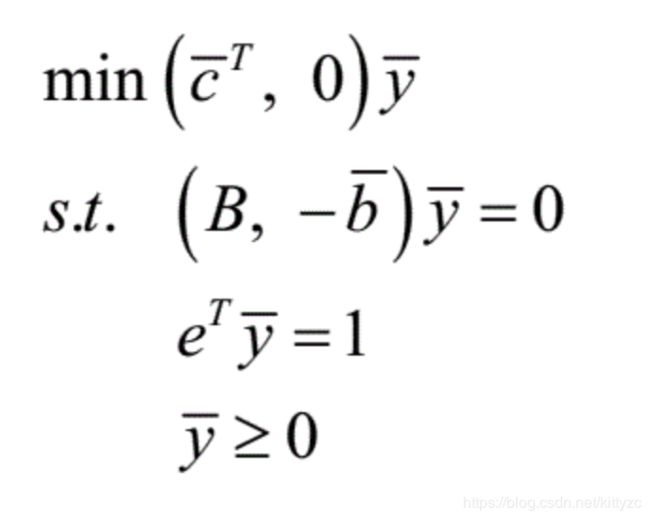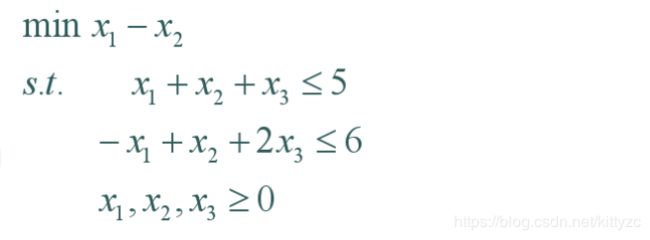运筹系列31:内点法python代码
1. 简介
用内点法求解线性规划问题理论上的计算复杂度为 O ( n 3.5 L 2 ) O(n^{3.5}L^2) O(n3.5L2),其中n是变量的维数,L是输入长度。而单纯形法本质上还是个搜索问题,其计算复杂度是 O ( 2 n ) O(2^n) O(2n)。
内点法总结起来有两大类,如下:
(1)使用拉格朗日法将不等式去除,然后使用KKT条件将原问题转为方程组,然后用牛顿法求解。
(2)类似信赖域方法,每次在一定范围(比如使用尺度变换生成一个球)内移动到最优位置,迭代进行。
基本概念可以参见:https://blog.csdn.net/WASEFADG/article/details/90376051

本文依次介绍Logarithmic barrier method,Affine scaling method,Projective method。
2. 经典的Barrier法
详细的介绍可以参考 https://zhuanlan.zhihu.com/p/32685234,对应的代码https://github.com/PrimerLi/linear-programming/tree/master/src
下面两张图是原理:
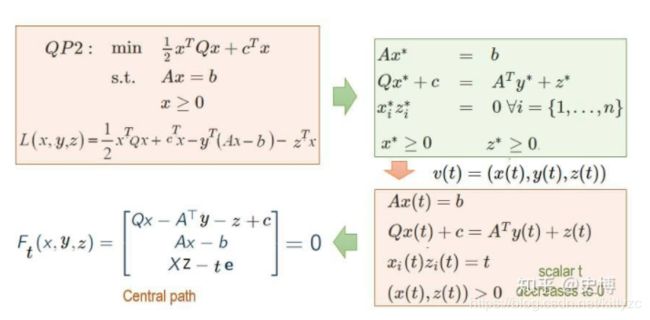
为了能够找到一个初始可行解,添加一个barrier函数:
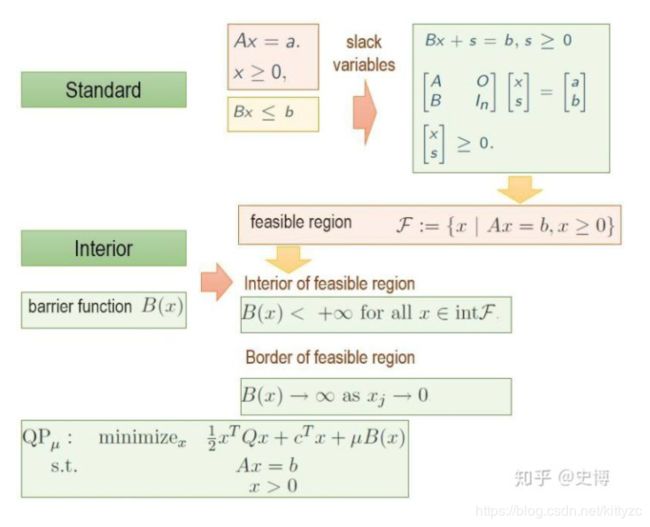
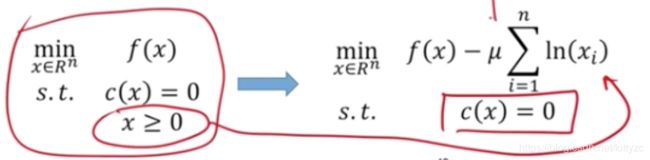
一般选用Logarithmic barrier method,如下。其中 ϕ ( x ) = − Σ i ln ( x i ) \phi(x)=-\Sigma_i \ln(x_i) ϕ(x)=−Σiln(xi)称为barrier函数。至于为什么用这个函数做barrier,可以参考这里
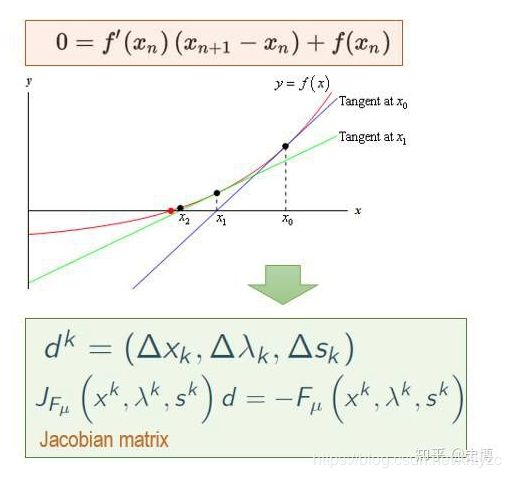
使用KKT条件进行转化,将最优化问题转换为求解方程。
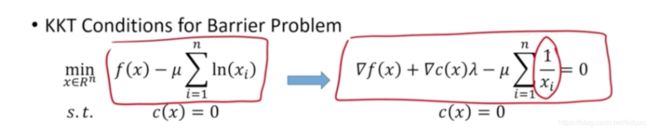
使用牛顿法求解,不同 μ \mu μ下的最优解构成的集合称为central path。
这里我们假设问题为线性:
min c T x \min c^Tx mincTx,s.t. A x ≤ b Ax\le b Ax≤b
barrier函数设置为 I t ( x ) = − l o g ( − u ) / t I_t(x)=-log(-u)/t It(x)=−log(−u)/t,目标函数为 t c x − Σ log ( − A x + b ) tcx-\Sigma\log(-Ax+b) tcx−Σlog(−Ax+b),并且有:


内点法是选取一个比较小的初始参数 t 0 t_0 t0,求出这个参数对应的解 x t 0 x_{t_0} xt0,逐步迭代从小 t 0 t_0 t0 到大 t t t可以得到一系列的解,最后得到的解 x t x_t xt称作是淬火解。这个解应该可以满足我们的精度需求。
def newton(t, A, b, c, x0):
maxIterationNumber = 50
eps = 1.0e-8
for count in range(maxIterationNumber):
slack = 1.0/(A.dot(x0) - b)
gradient = t*c - A.transpose().dot(slack) # 梯度
H = A.transpose().dot(np.diag(np.square(slack))).dot(A)
delta = np.linalg.inv(H).dot(gradient)
x0 = x0 - delta
error = np.linalg.norm(delta)
if (-error < eps):
break
return x0,error
def solver(t0, A, b, c, x0, factor):
upperBound = 1000*t0
t = [t0]
solutions = [x0]
eps = 1.0e-10
while(t0 < upperBound):
x0,error = newton(t0, A, b, c, x0)
solutions.append(x0)
print (x0)
t0 = factor*t0
t.append(t0)
if (error < eps):
break
return x0
下面是个例子:
min x + y \min x+y minx+y,
s.t.
0.81 x + 0.4 y ≥ 1 0.81x+0.4y\ge1 0.81x+0.4y≥1
0.4 x + 1.1 y ≥ 1 0.4x+1.1y\ge1 0.4x+1.1y≥1
x ≥ 0 x\ge0 x≥0
y ≥ 0 y\ge0 y≥0
用scipy直接求解:
from scipy import optimize
import numpy as np
optimize.linprog(c,A,b)
import os
import sys
import ReadFile
import random
A, b, c = ReadFile.read("linear-programming/data/A.txt", "linear-programming/data/b.txt", "linear-programming/data/c.txt")
x = np.array([0.1,0.2])
t = 1.0
m,n = A.shape
t = 1.0
initials = []
numberOfTests = 4
for i in range(numberOfTests):
x0 = np.zeros(len(c))
for i in range(len(x0)):
x0[i] = 1.4 + random.uniform(-0.3, 0.3)
initials.append(x0)
for i in range(len(initials)):
print ("******************* Test number = "+ str(i + 1) + " **************************")
factor = 1.2
solution = solver(t, A, b, c, initials[i], factor)
print ("Solution to the problem is: ")
print (solution)
print( "****************************************************************")
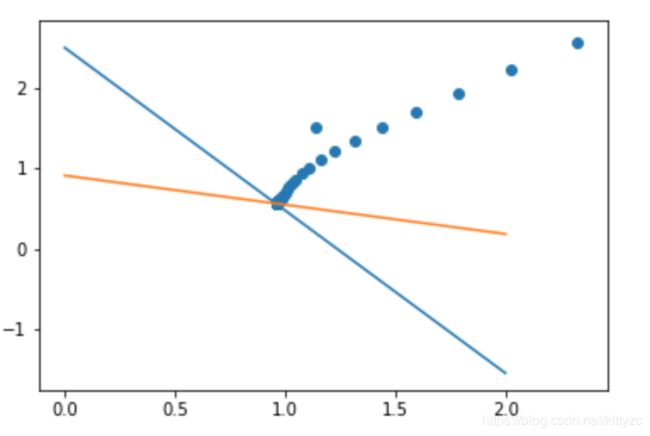
轨迹如下图:
当然,如果我们知道目标函数的jacobi和Hessian阵,则可以更简单,比如下面的例子:
min x 1 2 + x 2 2 \min x_1^2+x_2^2 minx12+x22
s.t. 2 x 1 + 3 x 2 ≤ 6 2x_1+3x_2\le6 2x1+3x2≤6
x 2 − 2 x 1 ≥ 1 x_2-2x_1\ge1 x2−2x1≥1
初始的 u = e u=e u=e,
import numpy as np
# function to minimize
def f(x, e):
x1 = x[0,0]
x2 = x[1,0]
return x1**2 + x2**2 - e*(np.log(6-2*x1-3*x2) + np.log(-1-2*x1+x2))
# Gradient of f
def grad(x, e):
x1 = x[0,0]
x2 = x[1,0]
grad = [2*x1 + e*(2./(-2*x1+x2-1) + 2./(-2*x1-3*x2+6)), 2*x2 + e*(1./(2*x1-x2+1) - 3./(-2*x1-3*x2+6))]
return np.array(grad).reshape((2,1))
# Hessian Matrix of f
def hessian(x, e):
x1 = x[0,0]
x2 = x[1,0]
H = [[2 + e*(4./((2*x1-x2+1)**2) + 4./(2*x1+3*x2-6)**2), e*(-2./((2*x1-x2+1)**2) + 6./(2*x1+3*x2-6)**2)], [e*(-2./((2*x1-x2+1)**2) + 6./(2*x1+3*x2-6)**2), 2 + e*(1./((2*x1-x2+1)**2) + 9./(2*x1+3*x2-6)**2)]]
return np.array(H)
def backtracking(x0, delta, e, c):
t = 1
while True:
x1 = x0 + t*delta
if f(x1,e) <= f(x0,e) + c*grad(x0,e).T @ (x1 - x0):
break
else:
t /= 2
return x1
def newton(x0, e, c, tol=1e-3):
assert(c > 0 and c < 1)
while True:
delta = - np.linalg.inv(hessian(x0, e)) @ grad(x0, e)
x1 = backtracking(x0, delta, e, c=c)
if np.linalg.norm(x1 - x0) < tol:
break
else:
x0 = x1
return x0
def interior_point(x0, e, c, tol=1e-5):
assert(tol > 0)
while True:
xe = newton(x0, e, c=c)
if e <= tol:
break
else:
x0 = xe
e /= 2
return x0
xe = interior_point(x0=np.array([-1, 1]).reshape((2,1)), e=1, c=0.5)
print("Minimum at:", xe.flatten())
print("Minimum:", f(xe,1))
3. PAS内点法
PAS内点法(Primal Affine Scaling)需要做一个近似转化,非常像信赖域方法。直观来看,是以当前点为中心点在椭球范围内沿着目标函数梯度方向投影在可行域零空间的向量前进。
标准形有两个约束条件,Ax=b的约束用可行域零空间来保证,而x≥0用椭球来保证。将范围限制在椭球内而不是多边形,是因为二次约束的性质比一次好,可以直接写出最优解的表达式。此外,我们的初始解离原点越远越好,这样构造的椭圆才能足够大,每次可以走足够远的距离。
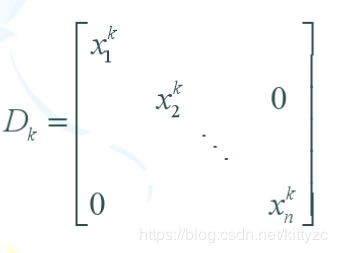
做一个线性变换,可以把椭球变成单位球,也就是下面的 x = D k y x=D_ky x=Dky

其中 D k D_k Dk是当前
上面的问题很容易求解。令可行域 A D k y = b AD_ky=b ADky=b的零空间法向量为 P k P_k Pk,则最优解为
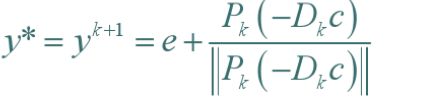
令 t = A D k t = AD_k t=ADk,则 P k = I − t T ( t t T ) − 1 t P_k=I-t^T(tt^T)^{-1}t Pk=I−tT(ttT)−1t。
将y转换为x,有:
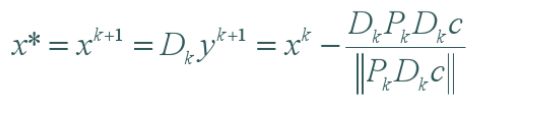
每次在范围为1的区域内不断前进,直至x收敛。总结下来步骤为:

下面是PAS方法的代码:
import numpy as np
def PAS(A,b,c,x,ite=1000,delta=0.001):
m,n = A.shape
D = x*np.eye(n,n)
res = np.diag(D)
for i in range(ite):
res = np.diag(D).copy()
t = A.dot(D)
p = np.eye(D.shape[1]) - t.T.dot(np.linalg.inv(np.matmul(t,t.T))).dot(t)
D+=(D.dot(p).dot(D).dot(c.T))/np.linalg.norm(p.dot(D).dot(c.T))
D = np.diag(D)*(np.eye(n,n))
resnew = np.diag(D)
if (sum(abs(resnew-res)))< delta:
break
return np.round(res,decimals=3)
x是初始解,注意不能取[0,0,…],否则中间会产生奇异矩阵。举个例子:
max 12 x 1 + 20 x 2 12x_1+20x_2 12x1+20x2
s.t.
0.2 x 1 + 0.4 x 2 ≤ 400 0.2x_1+0.4x_2\le 400 0.2x1+0.4x2≤400
0.5 x 1 + 0.4 x 2 ≤ 490 0.5x_1+0.4x_2\le 490 0.5x1+0.4x2≤490
x 1 , x 2 ≥ 0 x_1,x_2\ge 0 x1,x2≥0
输入如下:
A = np.matrix([[.2,.4,1,0],[.5,.4,0,1]])
b = np.matrix([[400],[490]])
c = np.matrix([12,20,0,0])
x = np.array([10,10,394,481])
最后的结果为:
array([300., 850., 0., 0.])
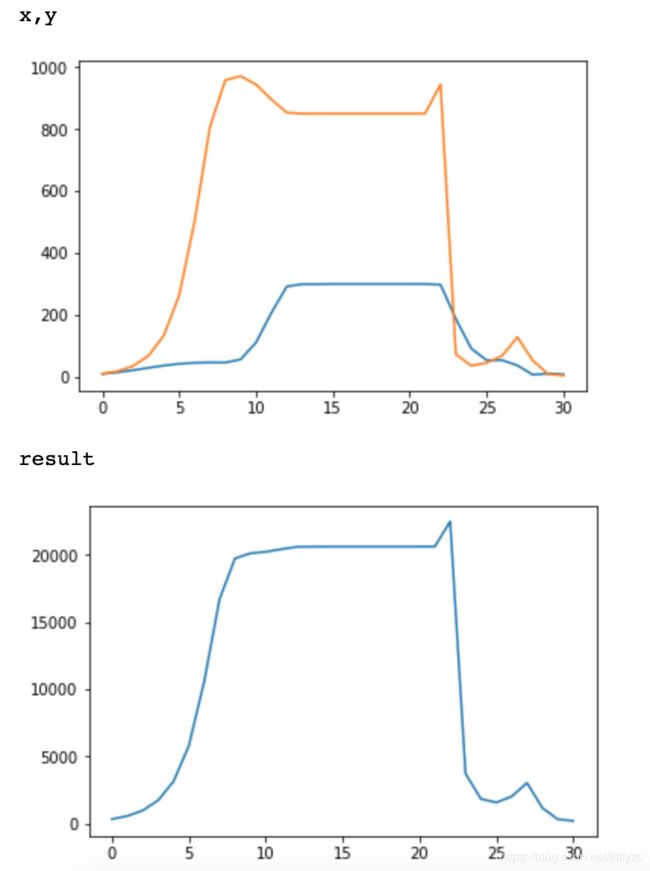
此外,由于误差累积的问题,delta不能设置的太小。下面是不设置delta,一直进行迭代的结果(实际是在第17次左右停止迭代)。第22迭代的小凸起是因为误差累积造成的,实际上已经到达边界了。
4. Karmarkar投影尺度算法
K投影法和PAS内点法的原理类似,我们不断做投影尺度变换将当前解置于中心位置,但是这个中心位置不再是PAS中的球心,而是一个单纯形的中心。
4.1 原理
单纯形是各坐标轴上单位向量构成的多边形S。我们可以定义一个特殊的投影变换,将任意一点 a a a变为S的中心 e / n e/n e/n:

4.2 目标函数转换
当目标函数不再优化时,迭代可以停止。这里用势函数代替原来的目标函数:

为什么要这么定义势函数呢,因为它有如下性质:

其中1的证明如下:

4.3 优化步长
接下来的步骤,用S的内接球B缩小一定比例 α \alpha α后取代S,和投影后的可行域 Ω \Omega Ω合起来求最优点:
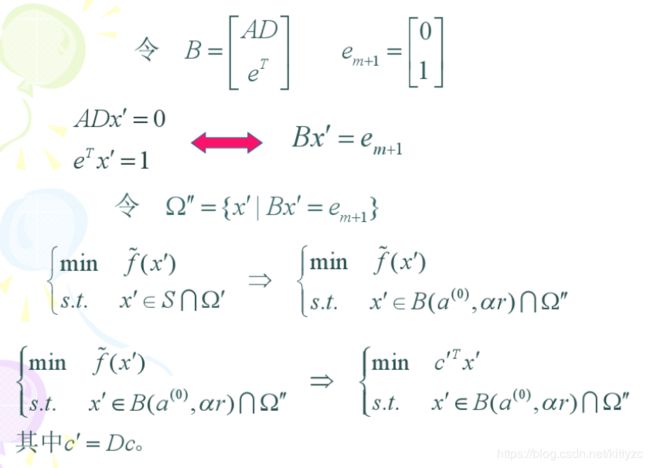
单纯形转化为球了,和1.2节的方法很类似了:

4.4 具体步骤:
4.4 一般问题的转换
首先呢,要将问题转化为标准形:
5. Mosek和scipy中的HSD法
对标准形进行一定转化,使用KKT条件将目标函数转为约束条件。KKT条件3个方程分别是:原问题可行、对偶问题可行、互补剩余。使用牛顿法求解非线性方程组的方法(和上面的牛顿法原理并不一样),并且对互补剩余条件进行一定松弛(一开始太猛,后面会难以收敛)进行迭代求解。
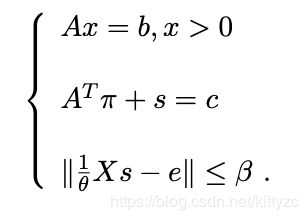
算法步骤为:

Mosek和SciPy中增加了一个约束(对偶问题和原问题在最优点时目标函数相等),并增加了两个松弛变量,非线性方程组(称为HLF)为:
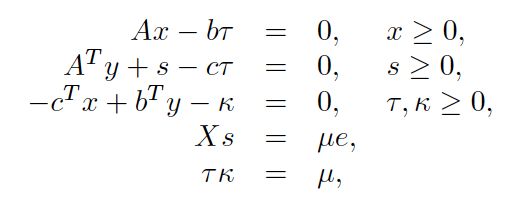
至于为什么要这么干,等后面慢慢研究吧。总之,对于一个HLF的一个可行内点解,我们可以得到原问题的解:
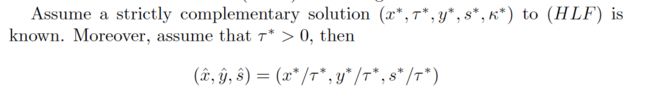
求解步骤类似,代码如下:
def _ip_hsd(A, b, c, c0, alpha0, beta, maxiter, tol):
iteration = 0
x, y, z, tau, kappa = np.ones(n),np.zeros(m),np.ones(n),1,1
rho_p, rho_d, rho_A, rho_g, rho_mu, obj = _indicators(A, b, c, c0, x, y, z, tau, kappa)
go = rho_p > tol or rho_d > tol or rho_A > tol
while go:
iteration += 1
# 求解梯度和步长,并进行更新。
gamma = beta * np.mean(z * x)
d_x, d_y, d_z, d_tau, d_kappa = _get_delta(A, b, c, x, y, z, tau, kappa, gamma)
alpha = _get_step(x, d_x, z, d_z, tau, d_tau, kappa, d_kappa, alpha0)
x = x + alpha * d_x
tau = tau + alpha * d_tau
z = z + alpha * d_z
kappa = kappa + alpha * d_kappa
y = y + alpha * d_y
# 计算误差,判断是否终止。这个终止条件的组合有些玄学啊。
rho_p, rho_d, rho_A, rho_g, rho_mu, obj = _indicators(A, b, c, c0, x, y, z, tau, kappa)
go = rho_p > tol or rho_d > tol or rho_A > tol
inf1 = (rho_p < tol and rho_d < tol and rho_g < tol and tau < tol * max(1, kappa))
inf2 = rho_mu < tol and tau < tol * min(1, kappa)
if inf1 or inf2 or teration >= maxiter:
break
return x / tau
def _get_step(x, d_x, z, d_z, tau, d_tau, kappa, d_kappa, alpha0):
i_x = d_x < 0
i_z = d_z < 0
alpha_x = alpha0 * np.min(x[i_x] / -d_x[i_x]) if np.any(i_x) else 1
alpha_tau = alpha0 * tau / -d_tau if d_tau < 0 else 1
alpha_z = alpha0 * np.min(z[i_z] / -d_z[i_z]) if np.any(i_z) else 1
alpha_kappa = alpha0 * kappa / -d_kappa if d_kappa < 0 else 1
alpha = np.min([1, alpha_x, alpha_tau, alpha_z, alpha_kappa])
return alpha
# 计算delta的trick有点多,等后面慢慢阅读文献。
def _get_delta(A, b, c, x, y, z, tau, kappa, gamma):
n_x = len(x)
r_P = b * tau - A.dot(x)
r_D = c * tau - A.T.dot(y) - z
r_G = c.dot(x) - b.transpose().dot(y) + kappa
mu = (x.dot(z) + tau * kappa) / (n_x + 1)
Dinv = x / z
M = A.dot(Dinv.reshape(-1, 1) * A.T)
alpha, d_x, d_z, d_tau, d_kappa = 0, 0, 0, 0, 0
rhatp = (1-gamma) * r_P
rhatd = (1-gamma) * r_D
rhatg = np.array((1-gamma) * r_G).reshape((1,))
rhatxs = gamma * mu - x * z
rhattk = np.array(gamma * mu - tau * kappa).reshape((1,))
solved = False
while(not solved):
solve_this = L if cholesky else M
p, q = _sym_solve(Dinv, solve_this, A, c, b, solve, splu)
u, v = _sym_solve(Dinv, solve_this, A, rhatd -
(1 / x) * rhatxs, rhatp, solve, splu)
if np.any(np.isnan(p)) or np.any(np.isnan(q)):
raise LinAlgError
solved = True
d_tau = ((rhatg + 1 / tau * rhattk - (-c.dot(u) + b.dot(v))) /
(1 / tau * kappa + (-c.dot(p) + b.dot(q))))
d_x = u + p * d_tau
d_y = v + q * d_tau
d_z = (1 / x) * (rhatxs - z * d_x)
d_kappa = 1 / tau * (rhattk - kappa * d_tau)
return d_x, d_y, d_z, d_tau, d_kappa
6. 参考文献
[1] Fourer, Robert. “Solving Linear Programs by Interior-Point Methods.” Unpublished Course Notes, August 26, 2005. Available 2/25/2017 at http://www.4er.org/CourseNotes/Book%20B/B-III.pdf
[2] Andersen, Erling D. “Finding all linearly dependent rows in large-scale linear programming.” Optimization Methods and Software 6.3 (1995): 219-227.
[3] Freund, Robert M. “Primal-Dual Interior-Point Methods for Linear Programming based on Newton’s Method.” Unpublished Course Notes, March 2004. Available 2/25/2017 at https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec14_int_pt_mthd.pdf
[4] Andersen, Erling D., and Knud D. Andersen. “The MOSEK interior point optimizer for linear programming: an implementation of the homogeneous algorithm.” High performance optimization. Springer US, 2000. 197-232.
[5] Andersen, Erling D., and Knud D. Andersen. “Presolving in linear programming.” Mathematical Programming 71.2 (1995): 221-245.
[6] Bertsimas, Dimitris, and J. Tsitsiklis. “Introduction to linear programming.” Athena Scientific 1 (1997): 997.
[7] Andersen, Erling D., et al. Implementation of interior point methods for large scale linear programming. HEC/Universite de Geneve, 1996.
使用 [1] Section 4.1.中的predictor-corrector method计算查找方向。计算过程用到了一些trick:首先使用Cholesky分解法代替LU因子法,如果失败,则尝试使用lstsq方法;其次如果是稀疏矩阵,则使用稀疏矩阵的spsolve方法,或者使用scikit-sparse的CHOLMOD方法。[1]的Section 5.3和[7]的Section 4.1-4.2介绍了一些改进方法。
接下来,[1] Section 4.1和4.3介绍了步长计算方法。