算法 —— 排序 —— 优先队列
- 优先队列
- 二叉堆
- 插入元素
- 删除最大元素
- 堆排序
- 1.堆的构造
- 2.堆的排序
- 总结
优先队列
【Priority Queue】
首先声明一下,优先队列是基于堆的完全二叉树,它和队列的概念无关。(它并不是队列,而是树)
并且,优先队列最重要的操作就是: 删除最大元素和插入元素,所以我们把精力集中在这两点上。(本文以最大堆为主讲述)
二叉堆
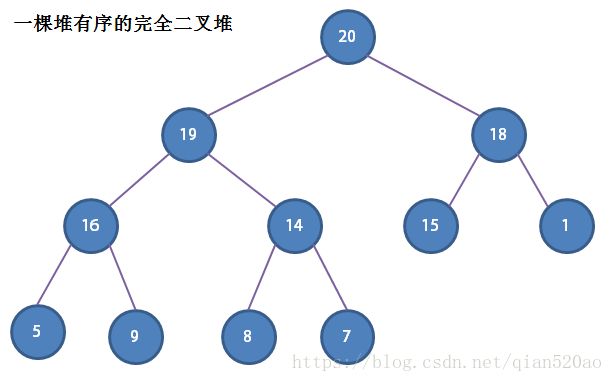
定义 : 当一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。
也可以说根结点(最顶部)是堆有序的二叉树中的最大结点。(最大堆)
如上图所示,一棵堆有序的完全二叉堆。
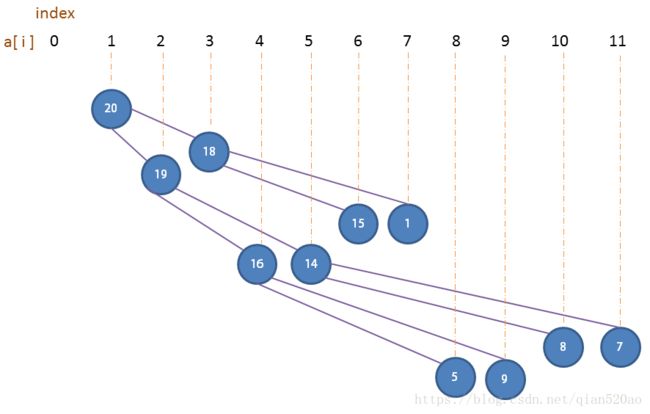
我们可以先定下根结点,然后一层一层向下,在每个结点的下方连接两个更小的结点。完全二叉树只用数组就可以表示。
根结点的索引(index)为 1 ,它的子结点在位置 2 和 3 ,并以此类推。
二叉堆是一组能够用堆有序的完全二叉堆排序的元素,并在数组中按照层级存储。(不使用数组的第一个位置)。
在一个堆中,位置 k 的结点的父结点的位置为[ k / 2 ] ,而它的两个子结点的位置则分别是 2k 或者 2k+1 。
我们用长度为 N+1 的私有数组 pq[ ] 来表示一个大小为 N 的堆,我们不会使用pq[ 0 ],堆元素放在pq[ 1 ] 至 pq[ N ]中。
插入元素
- 由下至上的堆有序化(上浮)
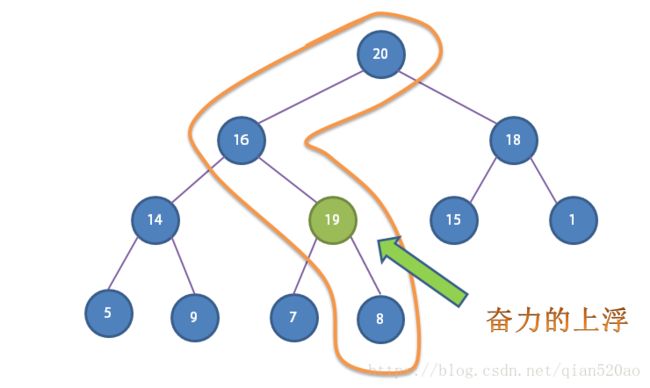
如果堆的有序状态因为某个结点变得比它的父结点更大而被打破,那么我们需要通过交换它和它的父结点来修复堆。
也就是说通常我们把元素插入在堆(数组)的末尾,然后不断的比较或交换它与它的父结点,直至根结点。
//上浮,插入元素使用。k表示元素索引
private void swim(int[] a, int k) {
while (k > 1 && a[k / 2] < a[k]) {
exch(a, k, k / 2);
k = k / 2;
}
}如果我们把堆想象成为一个严密的黑社会组织,每个每个子结点都表示一个下属,父结点表示为它的直接上级。
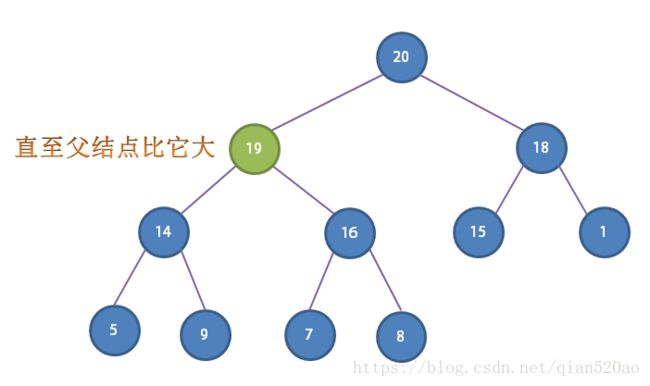
swim()表示一个很有能力的新人加入了组织并且逐级提升,(将能力不足的上级踩在脚下)直至它遇到了一个更强的领导。
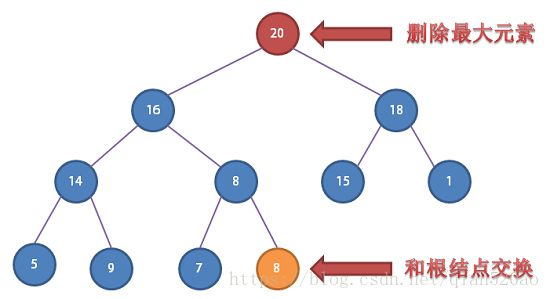
删除最大元素
- 由上至下的堆有序化(下沉)
与插入元素相同道理,如果新来的父结点(放置根结点)比子结点小,那么就需要不断的交换它和子结点的位置来修复堆。
所以我们删除最大元素的操作是 :
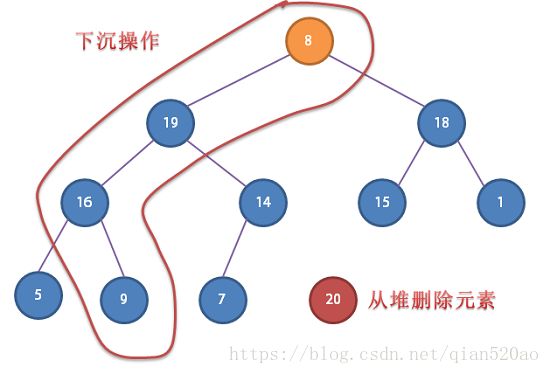
- 从数组顶端删除最大的元素
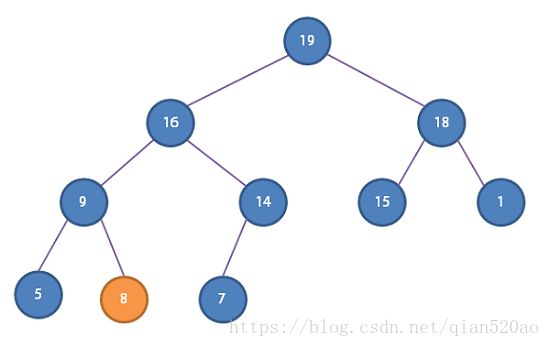
- 将数组的最后一个元素放到顶端,并让这个元素下沉( sink )到合适位置。
/**
* @param k 元素索引,1开始
* @param LEN 需排序的元素大小
*/
private static void sink(int[] a, int k, int LEN) {
while (2 * k <= LEN) {
int j = 2 * k; //j , j + 1 为子结点索引(2个子元素)
if (j < LEN && a[j] < a[j + 1])
j++;
if (a[k] > a[j]) { //如果新加入的结点大于子结点,则终止
break;
}
exch(a, k, j); //否则交换父结点与子结点位置
k = j; //继续比较子结点的子结点
}
} private static int[] delMax(int[] a) {
exch(a, 1, a.length - 1);// 最大元素和最后一个结点交换
// a[LEN] = null;// 防止对象游离,即回收对象
a = Arrays.copyOf(a, a.length - 1);
sink(a, 1, a.length - 1);
return a;
}优先队列由一个基于堆的完全二叉树表示,存储于数组pq[ 1..N ]中,pq [0 ]没有使用。
- 插入元素:我们将新元素添加在数组最后,用
swim()(index = LEN-1)恢复堆的秩序。 - 删除最大元素 : 我们获得最大元素(索引为1),并将最大元素和数组的最后一个元素交换位置,用
sink()(index = 1) 恢复堆的秩序。
堆排序
堆排序可以分为两个阶段: 堆构造 和 堆排序
首先我们要将原始数组重新组织安排进入堆中,使数组成为堆有序数组。即堆有序的完全二叉堆。
然后我们再将该数组进行排序,使数组成为有序数组。
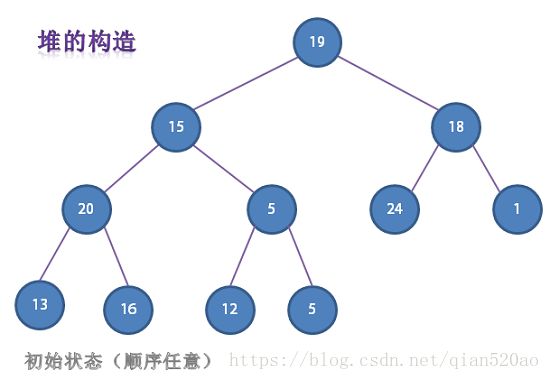
1.堆的构造
由N个给定的元素构造一个堆,我们可以很容易的从左至右遍历数组,使用swim()将元素一个个插入到堆中。
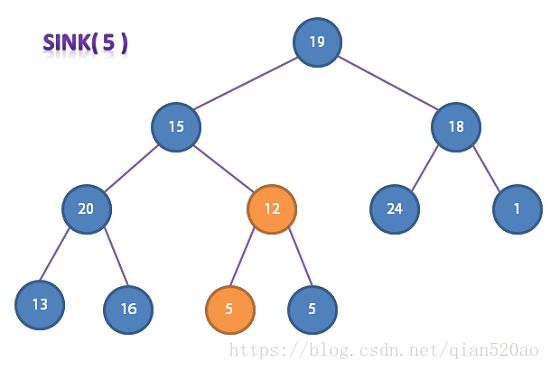
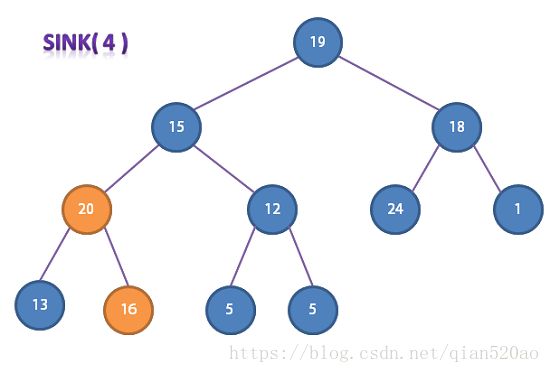
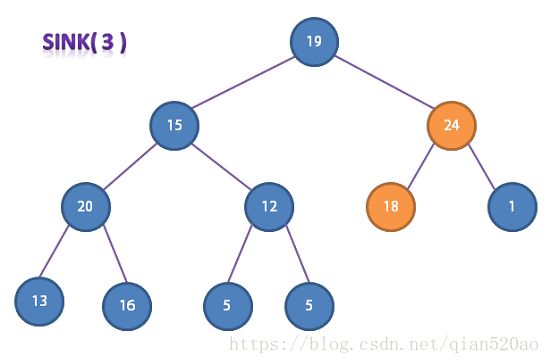
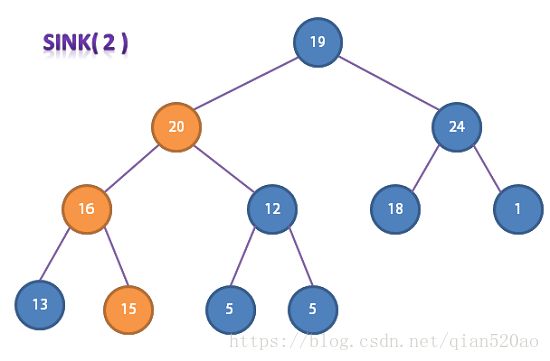
但是一个更高效的办法是从右到左,使用sink()函数构造堆,并且我们只需从 LEN / 2 的地方开始往左遍历即可。
//堆构造
for (int k = LEN / 2; k >= 1; k--) {
sink(a, k, LEN);
}
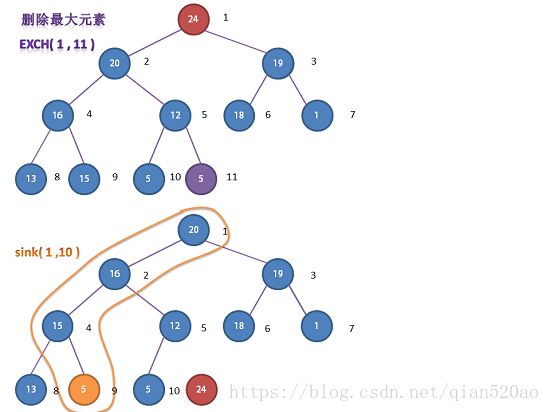
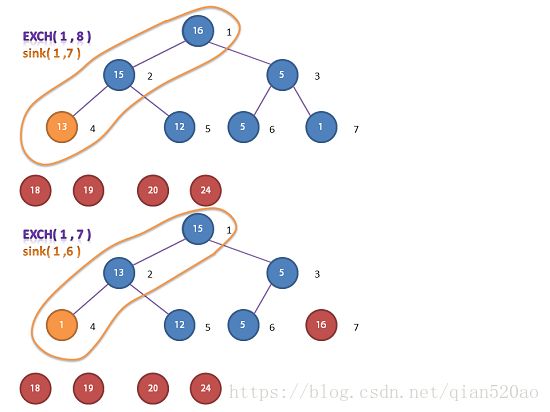
2.堆的排序
我们可以再温习一下删除最大元素的思想:
- 我们将堆有序的 第一个元素 pq [ 1 ] 删除
- 并且将数组的最后一放置顶端,使用
sink()修复堆。
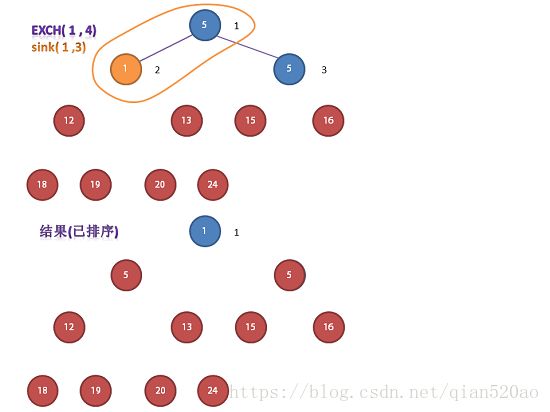
也就是说我们每次删除的元素都是最大的,那么我们只要将依次删除的这些最大元素收集起来,那么也就是数组有序了。
堆排序的主要工作都是在第二阶段(第一阶段是堆构造)完成的。
我们将堆的最大元素删除,然后放入堆缩小后的数组中空出位置。(这个过程和选择排序有些类似,但所需的比较要少的多)
public class S_优先队列 {
public static void main(String[] args) {
int[] a = { 0, 9, 6, 8, 10, 2, 11, 1, 5, 7, 4, 2 };// 11个元素,a[0] 不用
int LEN = a.length - 1;
for (int k = LEN / 2; k >= 1; k--) {
sink(a, k, LEN);
}
System.out.println("--构造堆--" + Arrays.toString(a));
while (LEN > 1) {
exch(a, 1, LEN--);
sink(a, 1, LEN);
}
System.out.println("--堆排序--" + Arrays.toString(a));
// a = delMax(a);
// System.out.println("--删除最大元素--" + Arrays.toString(a));
}
/**
* @param k 元素(非数组)下标,1开始
* @param LEN 需排序的元素大小
*/
private static void sink(int[] a, int k, int LEN) {
while (2 * k <= LEN) {
int j = 2 * k;
if (j < LEN && a[j] < a[j + 1])
j++;
if (a[k] > a[j]) {
break;
}
exch(a, k, j);
k = j;
}
}
/**
* 上浮,插入元素使用
*/
private void swim(int[] a, int k) {
while (k > 1 && a[k / 2] < a[k]) {
exch(a, k, k / 2);
k = k / 2;
}
}
private static int[] delMax(int[] a) {
exch(a, 1, a.length - 1);// 最大元素和最后一个结点交换
// a[LEN] = null;// 防止对象游离,即回收对象
a = Arrays.copyOf(a, a.length - 1);
sink(a, 1, a.length - 1);
return a;
}
public static void exch(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
总结
堆排序在排序复杂度的研究中有着重要的地位。因为它在最坏的情况下也能保证使用 ~2NlgN 次比较和恒定的额外空间。
并且它能在 插入操作 和 删除最大元素操作混合动态场景中保证对数级别的运行时间。
延伸 —– 最小堆
另外本文所述的为最大堆(大顶堆),即根结点最大。如果根结点为最小,它的子结点都比父结点大,那么称为最小堆(小顶堆)
从 n 个无序数中选出 m 个最大数
最小堆 : 头 m 个数建立 size = m 的最小堆,(根结点最小),后续数小于根结点则抛弃;大于根结点则插入并替换。
快排 : 当大于分界的个数大于 m ,则抛弃小于分界的部分。当大于分界的个数小于 m ,则全部保留,并且在小于的部分找出剩余的 n - m 个最大数。