LeetCode214——最短回文串

我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/shortest-palindrome/description/

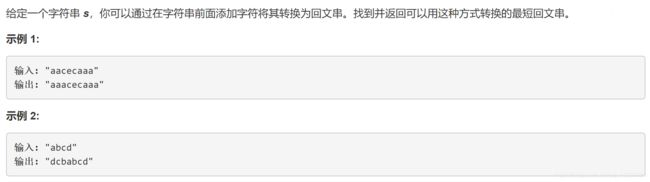
题目描述：

知识点：回文字符串、KMP算法

思路一：暴力破解法

要找到满足题目要求的最短回文串，本质是要找到最长的回文子串，该子串的左端点与字符串s的左端点重合。

时间复杂度是O(n ^ 2)，其中n为字符串s的长度。空间复杂度是O(n)。

JAVA代码：

class Solution {
    public String shortestPalindrome(String s) {
        int index = -1;
        for(int i = s.length() - 1; i >= 0; i--){
            if(isPalindrome(s.substring(0, i + 1))){
                index = i;
                break;
            }
        }
        String result = reverse(s.substring(index + 1));
        return result + s;
    }
    private String reverse(String s){
        StringBuilder stringBuilder = new StringBuilder(s);
        return stringBuilder.reverse().toString();
    }
    private boolean isPalindrome(String s){
        for(int i = 0; i < s.length() / 2; i++){
            if(s.charAt(i) != s.charAt(s.length() - 1 - i)){
                return false;
            }
        }
        return true;
    }
}

LeetCode解题报告：

思路二：递归解法

左指针i初始化为0，右指针j从n - 1递减到0，其中n为字符串s的长度，一旦遇上i指向的字符与j指向的字符相等时，令i指针加1。

递归出口：

如果i指针最后的值等于n，说明字符串s本身就是回文串，直接返回s即可。

递归过程：

首先明确一点：我们所要寻找的最长回文子串，该子串的左端点与字符串s的左端点重合，一定在[0, i)范围内。

考虑两种极端情况，第一种情况：字符串s本身就是回文串，显然满足条件。第二种情况：在遍历过程中，不存在i指向的字符与j指向的字符相等的情况，除了i和j相等时，这种情况我们得到的i是1。显然也满足条件。

考虑一般性情况：假设我们所要寻找的最长回文子串不在[0, i)范围内，即存在回文串其在[0, k)范围内，其中k > i。那么显然，在我们遍历的过程中，即使j在[k, n - 1]范围时不存在i指向的字符与j指向的字符相等的情况，最终i的值也会到达k，即i >= k，这显然矛盾了，因此该结论成立。

由上述结论，我们得出：[i, n - 1]范围内的子串一定不是我们所要寻找的最长回文子串的一部分。

这样，我们就可以递归地反转[0, i)范围内的子串来拼接出结果。

时间复杂度是O(n ^ 2)，其中n为字符串s的长度。空间复杂度是O(n)。

JAVA代码：

class Solution {
    public String shortestPalindrome(String s) {
        int i = 0;
        for(int j = s.length() - 1; j >= 0; j--){
            if(s.charAt(j) == s.charAt(i)){
                i++;
            }
        }
        if(i == s.length()){
            return s;
        }
        return reverse(s.substring(i)) + shortestPalindrome(s.substring(0, i)) + s.substring(i);
    }
    private String reverse(String s){
        StringBuilder stringBuilder = new StringBuilder(s);
        return stringBuilder.reverse().toString();
    }
}

LeetCode解题报告：

思路三：KMP算法

将原字符串s和其逆序字符串用“#”拼接在一起，利用KMP算法中next数组的求法求得拼接出的新字符串的最长相同前后缀，就是原字符串s中最长的回文子串，该子串的左端点与字符串s的左端点重合。

这个问题是一个动态规划问题：求取字符串s中的最长相同前后缀（不能是其本身）

状态定义：

f(x) -------- 字符串s中[0, x]范围内的最长相同前后缀（不能是其本身）的长度

状态转移：

首先是初始化，f(0)显然是0，因为[0, 0]范围内的字符串长度为1，其最长相同前后缀根本不存在。

对于i在[1, n - 1]（其中n为字符串s的长度）范围内的值：

（1）令temp记录f(x - 1)的值，如果temp大于0且s中temp位置的字符和第i个字符不相同，那么我们就需要重设temp的值为f(temp - 1)。

（2）如果s中第i个字符与第temp个字符相同，令temp自增1。

（3）f(i) = temp。

上述状态转移过程可能很难理解，以一个例子——“ABABCABAA”来说明，其子串如下：

A -------------------------------------------------- 0

AB ------------------------------------------------ 0

ABA ---------------------------------------------- 1

ABAB -------------------------------------------- 2

ABABC ------------------------------------------ 0

ABABCA ---------------------------------------- 1

ABABCAB -------------------------------------- 2

ABABCABA ------------------------------------ 3

ABABCABAA ---------------------------------- 1

对由ABAB求得ABABC这个过程进行分析：

C和A不相等，因此结果不可能是3，如果是ABABA，则结果是3。ABAB的结果是2，因此我们知道AB和AB相同，但是第一个AB之后跟着的是A，依然和C不相同。我们继续看AB，AB的结果是0，因此我们知道AB中A和B不相同，而C和A不相同，因此结果是0。

对由ABABCABA求得ABABCABAA这个过程进行分析：

A和B不相等，因此结果不可能是4，如果是ABABCABAB，则结果是4。ABABCABA的结果是3，因此我们知道ABA和ABA相同，但是第一个ABA之后跟着的是B，依然和A不相同。我们继续看ABA，ABA的结果是1，但是第一个A之后跟着的是B，依然和A不相同。我们继续看A，结果是0，结束while循环。这个A和A相同，因此其值加1变成1。

时间复杂度和空间复杂度均是O(n)，其中n为字符串s的长度。

JAVA代码：

class Solution {
    public String shortestPalindrome(String s) {
        String rev = reverse(s);
        String temp = s + "#" + rev;
        int[] next = getNext(temp);
        return rev.substring(0, rev.length() - next[temp.length() - 1]) + s;
    }
    private String reverse(String s){
        StringBuilder stringBuilder = new StringBuilder(s);
        return stringBuilder.reverse().toString();
    }
    private int[] getNext(String s){
        int[] result = new int[s.length()];
        result[0] = 0;
        for(int i = 1; i < result.length; i++){
            int temp = result[i - 1];
            while(temp > 0 && s.charAt(i) != s.charAt(temp)){
                temp = result[temp - 1];
            }
            if(s.charAt(i) == s.charAt(temp)){
                temp++;
            }
            result[i] = temp;
        }
        return result;
    }
}

LeetCode解题报告：