数字电子技术逻辑运算
数字电子技术学习笔记
- 第一章 数制与编码
- 第二章 基本逻辑运算与集成逻辑门
- 2.1 基本概念
- 2.1.1逻辑变量与逻辑函数
- 2.1.2真值表
- 2.2 三种基本逻辑运算
- 2.2.1与逻辑(与运算、逻辑乘)
- 2.2.2 或逻辑(或运算、逻辑加)
- 2.2.3 非逻辑(非运算、逻辑反)
- 2.3 常用额复合逻辑
- 2.3.1 “与非”逻辑
- 2.3.2 “或非”逻辑
- 2.3.3 “与或非”逻辑
- 2.3.3 “异或逻辑”与“同或逻辑”
- 2.4集成逻辑门电路
- 2.4.1 TTL集成逻辑电路
- 2.4.2 CMOS集成逻辑电路
- 2.4.3 集成逻辑门电路的特性与参数
- 2.4.4 开路门与三态门
- 2.4.5 集成逻辑门在使用的实际问题
- 第三章 布尔代数与逻辑函数化简
- 3.1.1 基本公式
- 3.1.2 基本法则
- 3.1.2 基本公式的应用
- 3.2逻辑函数的代数化简
- 3.2.1 逻辑函数与逻辑图
- 3.2.2 逻辑函数的化简原则
- 3.2.3与或逻辑函数的简化
- 3.3 卡诺图化简
- 3.3.1 卡诺图化简的基本原理
- 3.3.2 逻辑函数的标准式——最小项
- 3.3.3 卡诺图结构
- 2.3.4 逻辑函数的卡诺图表示法
- 3.3.5 相邻项合并规律
- 3.3.6
- 3.3.7其他逻辑函数式的化简
- 3.3.8无关项及其应用
- *3.3.9 有原变量无反变量的逻辑函数的化简
- 第四章 组合逻辑电路
- 第五章 触发器
- 第六章 时序逻辑电路
- 第七章 脉冲波形的产生于变换
- 第八章 数/模与模/数转换
- 第九章 半导体存储器和可编程逻辑器件
第一章 数制与编码
第二章 基本逻辑运算与集成逻辑门
基本逻辑运算及实现这些基本逻辑运算的集成电路——集成逻辑门。
“逻辑”一词首先见于逻辑学。逻辑学属于哲学领域,它研究逻辑思维推理的规律。逻辑代数是逻辑学的基本上发展的一门学科,它采用一套符号来描述逻辑思维,并将复杂的逻辑问题抽象为一种简单的符号演算,拜托了冗繁的文学描述。
2.1 基本概念
2.1.1逻辑变量与逻辑函数
所有逻辑命题必须满足二值律,逻辑命题只有两种逻辑值,不是逻辑真就是逻辑假,不存在第三种似是而非的值。
2.1.2真值表
由于逻辑变量只有两种取值0或1,因此,可以用一种很简单的表格来描述函数的全部真、伪关系,所以称这种表为真值表。
真值表的左侧一栏为逻辑变量的所有组合,右侧一栏为所得真值表的结果
表2-1 真值表格式
| 组合 | A | B | C | D | F |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 0 | 0 |
| 8 | 0 | 1 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 |
| 10 | 1 | 0 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 0 | 0 |
| 12 | 1 | 0 | 1 | 1 | 0 |
| 13 | 1 | 1 | 0 | 0 | 0 |
| 14 | 1 | 1 | 0 | 1 | 0 |
| 15 | 1 | 1 | 1 | 0 | 0 |
| 16 | 1 | 1 | 1 | 1 | 1 |
2.2 三种基本逻辑运算
在实际中可能遇到的逻辑问题是千变万化的,有的数字系统如计算机还十分复杂。但仔细分析,他们可能用三种逻辑运算综合起来的。这三种基本运算就是:逻辑乘——“与运算”;逻辑加——“或运算”;逻辑非——“非运算”。
在这三种基本的逻辑运算的基础上将扩展到:与非、或非、 与或非 、异或 和 同或 几种常用的复合逻辑。上述逻辑运算的电路又称为逻辑电路,常常成为门电路。
2.2.1与逻辑(与运算、逻辑乘)
与逻辑(逻辑乘)指出,必须所有前提条件同时具备,结论成立,也就是全为真(1)总的结果为真(1)。
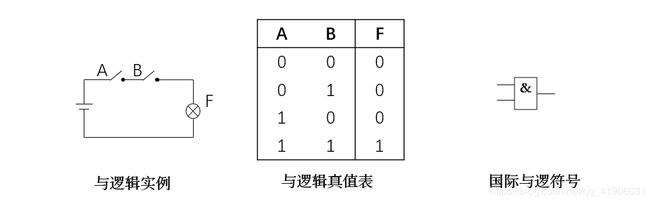
运用“与”逻辑式,可将两逻辑变量的运算几多表示如下:
0 · 0 = 0 ; 0 · 1 = 0 ; A · 0 = 0 ;A· 1 = A;
1 · 0 = 0 ; 1 · 1 = 1 ; A · A = A ;A· A ‾ \overline{A} A = 0;
总结:逻辑与的时候遇到0结论为0
2.2.2 或逻辑(或运算、逻辑加)
“或”运算表示的逻辑关系式:只要一个前提条件具备了,结论就成立。

0 + 0 = 0 ; 0 + 1 = 1 ; A + 0 = A ;A+ 1 = 1;
1 + 0 = 1 ; 1 + 1 = 1 ; A + A = A ;A + A ‾ \overline{A} A = 1;
总结:逻辑或的时候遇到1结论为1
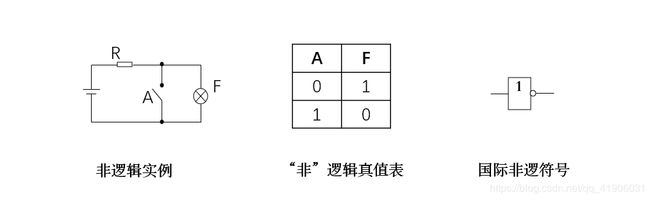
2.2.3 非逻辑(非运算、逻辑反)
“非”运算表示否定,它是逻辑运算中一种特有的形式,在逻辑代数中起着十分重要的作用。
2.3 常用额复合逻辑
与、或、非是逻辑代数中最基本的三种运算,任何复杂的逻辑函数都可以通过与、或、非的组合构成。我们称与、或、非是一个完备集。
2.3.1 “与非”逻辑
“与非”逻辑式“与”逻辑和“非”逻辑的组合,先“与”再“非”。
与非逻辑表达式:F = A ⋅ B ‾ \overline{A · B} A⋅B

2.3.2 “或非”逻辑
“或非”逻辑式“或”逻辑和“非”逻辑的组合,先“或”后“非”。
或非逻辑表达式F = A + B ‾ \overline{A + B} A+B

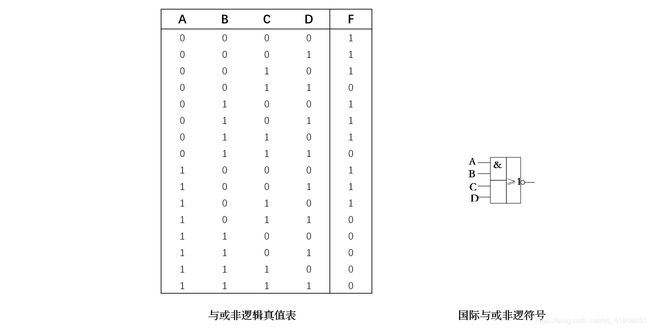
2.3.3 “与或非”逻辑
“与或非”逻辑式“与”、“或”、“非”三种基本逻辑组合先“与”再“或”最后“非”。
与或非表达式:或非逻辑表达式F = A B + C D ‾ \overline{AB + CD} AB+CD
2.3.3 “异或逻辑”与“同或逻辑”
-
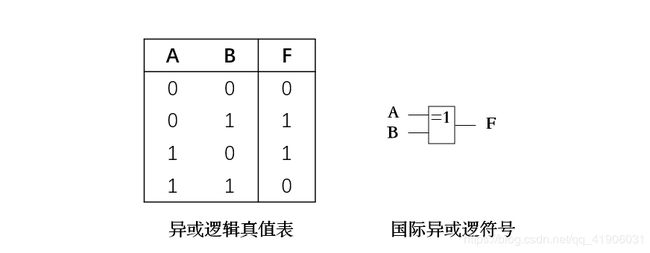
异或
“异或” 逻辑是指输入在二变量的情况下,输入两变量相异 时输出为“1”;相同时输出为“0”。
异或逻辑表达式为:F1 = A B ‾ \overline{B} B + A ‾ \overline{A} AB = A ⊕ B
-
同或
“同或” 逻辑是指输入在两变量的情况下,输入两变量相同时输出为“1”;相异时输出为“0”。
异或逻辑表达式为:F2 = AB + A ‾ \overline{A} A B ‾ \overline{B} B = A ⊙ B

-
“异或逻辑” 和 “同或逻辑” 互为反函数
A ⊕ B = A ⊙ B ‾ \overline{A ⊙ B} A⊙B; A ⊙ B = A ⊕ B ‾ \overline{A ⊕ B} A⊕B
A ‾ \overline{A} A B + A B ‾ \overline{B} B = ~ ( A ‾ \overline{A} A B ‾ \overline{B} B +A B)
A ‾ \overline{A} A B ‾ \overline{B} B + A B = ~( A ‾ \overline{A} A B + A B ‾ \overline{B} B)
2.4集成逻辑门电路
用以实现基本逻辑运算和符合逻辑运算的单元电路称为门电路。
把若干个有源器件和无源器件及其连线,按照一定的功能要求,制作在同一块半导体基片上,这样的产品叫做集成电路。若它完成的功能是逻辑功能或数字功能,则称为逻辑集成电路或数字集成电路。最简单的数字集成电路数集成逻辑门。
集成逻辑门,按照其组成的有源元件的不同可分为两大类:一类是双极性晶体管逻辑门;另一类是单极性绝缘栅场效应管逻辑门,简称MOS门。
2.4.1 TTL集成逻辑电路
TTL电路存在最大的问题就是功耗大。因此它只能制作小规模集成电路(Small Scale Integration,简称 SSI,其中仅包含10个以内的门电路)和中规模集成电路(Medium Scale Integration,简称 MSI,其中包含10~100个门电路),而 无法制 作成大规模集成电路(Large Scale Integration,简称 LSI ,其中包含100~10000个门电路)和超大规模集成电路(Very Large Scale Integration,简称 CLSI ,其中包含10000个门电路以上的电路)。
2.4.2 CMOS集成逻辑电路
CMOS逻辑门电路是在TTL电路之后出现的一种广泛应用的数字集成器件。按照器件结构的不同形式,可以分为NMOS、PMOS、CMOS三种逻辑门电路。
几乎所有的超大规模存储器以及PLD(可编程逻辑器件)器件都采用CMOS工艺制造,且费用较低。
2.4.3 集成逻辑门电路的特性与参数
- 传输特殊性
传输特性是指其电压uo。随输入电压ui变化的曲线,反相器的电压传输特性。 - 输出高电平UOH、输出低电平UOL
对于典型功过电压为5V的74HC系列的CMOS逻辑电路,UOH = 5V, UOL = 0V。 - 噪声容限
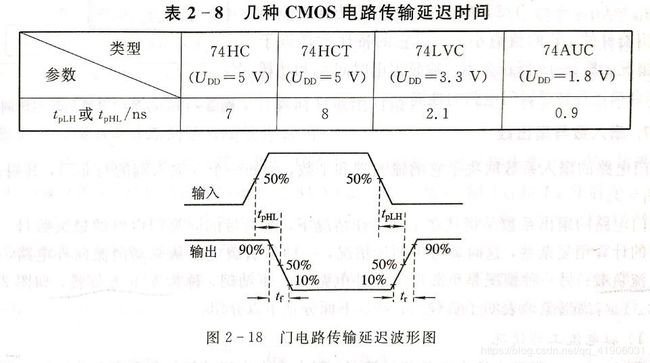
噪声容限表示门电路的抗干扰人力。 - 传输延迟时间
传输延迟时间是表征门电路开关速度的参数,它说明门电路大脉冲波形的作用下,其传输波形相对于输入波形延迟了多少时间。
- 功耗
功耗是门电路的重要参数之一。功耗有 静态功耗 和 动态功耗 。所谓静态功耗,指的是当电路的输出没有状态转换时的功耗。 - 延时——功耗积
- 扇入数和扇出数
门电路的扇入系数取决于它的输入端和个数。
门电路的删扇出数要考虑两种情况,一种是负载电路从驱动门电路流向外电路,称为拉电流负载;另外一种情况是负载电路从电路流入驱动门,称为灌电流负载。
2.4.4 开路门与三态门
1.开路门
开路门有TTL的集电极开路门(OC门)和CMOS的漏极开路门(OD)。

2.三态门
三态门的出现,是为了适应数字系统采用总线结构的需要。三态门具有三种状态,除了高电平(“1”)、低电平(“0”)外,还有高阻态。

2.4.5 集成逻辑门在使用的实际问题
- 接口电路
接口电路的作用是通过逻辑电平的转换, 把不同的逻辑值的电路(如TTL和CMOS门电路)连接起来;或者用来驱动集成电路本身驱动不了的大电流及大功率负载;也可用来切断干扰源通道,增强矿干扰能力。
- 抗干扰措施
利用逻辑门电路(CMOS或TTL)做具体的电路设计是,还应当注意下列几个实际问题:
1)多余输入端的处理措施
集成逻辑门电路子使用时,一般不让多余的输入端悬空,以防止干扰信号输入。
2)去耦合滤波电容
数字电路或系统往往有多片逻辑门电路构成,由一公共的直流电源供电。这种状态是非理想的,一般由整流稳压电路供电,具有一定的内阻抗。当数字电路再高、低状态之间交替变换时,产生较大的脉冲电流或尖峰电流,当它们流经公共的内阻抗时,必将产生相互影响,甚至式逻辑功能发生错乱。一种常用的处理方法是采用去耦滤波电容,用10~100μF的大电容接在直流电源与地之间,滤除干扰信号。除此之外,在每一集成芯片的电源与地之间接一个0.1μF的电容器以滤除开关噪声。
3)接地和安装工艺
正确的接地技术对于降低电路噪声是很重要的。方法是将电源地域信号地分开,现将信号地汇集在一点,然后再将二者用最短的导线连在一起,以免含有多种脉冲波形(函尖峰电流)的大电流引导某数字器件的额输入端而破坏系统正常的逻辑功能。此外,当系统中同时由模拟和数字两种器件时,同样需将二者的第分别连在一起,然后再选用一个合适的共同连接点,以免除二者之间的影响。必要时,也可以设计模拟和数字两块电路板,个备直流电源,然后将二者的地恰当的连接在一起。在印制电路板的设计或安装中,要注意连线尽可能短,以减少接线电容产生寄生反馈而引起的寄生振荡。
此外CMOS期间在使用和储藏过程中要注意静电感应导致损伤的问题。静电静电屏蔽是常用的防护措施。
第三章 布尔代数与逻辑函数化简
布尔代数又叫逻辑代数或开关代数,它是英国人乔治·布尔(G·Boole)与1849年首建立的。
3.1.1 基本公式
| 公式名称 | 逻辑与 | 逻辑或 |
|---|---|---|
| 1. 0-1律 | A · 0 = 0 | A + 1 = 1 |
| 2. 自等律 | A · 1 = A | A + 0 =A |
| 3. 等幂律 | A · A = A | A + A = A |
| 4. 互补律 | A · A ‾ \overline{A} A = 0 | A + A ‾ \overline{A} A = 1 |
| 5. 交换律 | A · B = B · A | A + B = B + A |
| 6. 结合律 | A · (B · C) = (A · B) · C | A + (B + C) = (A + B) + C |
| 7. 分配律 | A(B + C) = AB + AC | A + BC = (A + B)(A + C) |
| 8. 吸收律(1) | (A + B)(A + B ‾ \overline{B} B) = A | AB + A B ‾ \overline{B} B = A |
| 9. 吸收律(2) | A(A + B) = A | A + AB = A |
| 10. 吸收律(3) | A( A ‾ \overline{A} A + B) = AB | A + A ‾ \overline{A} AB = A + B |
| 11. 多余项定律 | (A + B)( A ‾ \overline{A} A + C)(B + C) = (A + B)( A ‾ \overline{A} A + C) | AB + A ‾ \overline{A} AC + BC = AB + A ‾ \overline{A} AC |
| 12. 求反律 | A B ‾ \overline{AB} AB = A ‾ \overline{A} A + B ‾ \overline{B} B | A + B ‾ \overline{A+B} A+B = A ‾ \overline{A} A · B ‾ \overline{B} B |
| 13.否否律 | ~( A ‾ \overline{A} A) = A |
吸收率(1)的证明: AB + A B ‾ \overline{B} B = A(B + B ‾ \overline{B} B);(因为B + B ‾ \overline{B} B = 1)
吸收率(2)的证明: A + AB = A(B + 1);(因为 B + 1 = 1)
吸收率(3)的证明: A + A ‾ \overline{A} AB = A + B; 引用 分配率
多余项证明: AB + A ‾ \overline{A} AC + BC = AB + A ‾ \overline{A} AC + BC(A + A ‾ \overline{A} A) = AB + A ‾ \overline{A} AC + ABC + A ‾ \overline{A} ABC = AB(1 + C) = A ‾ \overline{A} AC(1 + B) = AB + A ‾ \overline{A} AC;
求反律又称摩根定律
3.1.2 基本法则
-
带入法则
逻辑等式中的任何变量A,都可以用另一个函数Z代替,等式仍然成立。
代入法则可以扩大基本同时的应用范围
A 1 + A 2 + A 3 + … … + A n ‾ \overline{A1 + A2 + A3 + …… + An} A1+A2+A3+……+An = A 1 ‾ \overline{A1} A1 · A 2 ‾ \overline{A2} A2 · A 3 ‾ \overline{A3} A3 · …… · A n ‾ \overline{An} An
A 1 ⋅ A 2 ⋅ A 3 ⋅ … … ⋅ A n ‾ \overline{A1 · A2 · A3 · …… · An} A1⋅A2⋅A3⋅……⋅An = A 1 ‾ \overline{A1} A1 + A 2 ‾ \overline{A2} A2 + A 3 ‾ \overline{A3} A3 + …… + A n ‾ \overline{An} An -
对偶法则
对于任何一个逻辑表达式F,如果将其中的“ · ”换成“ + ”,“ + ”换成“ · ”,“ 1 ”换成“ 0 ”, “ 0 ”换成“ 1 ”,并保持原先的逻辑优先级,变量不变,两变量以上的非号不动,则可能原函数F的对偶式G, 且F和G互为对偶式。 则通过对偶式之前表中的基本公式记忆一般即可,另一半可通过对偶式进行求出。注意在求对偶式时保持原式的逻辑优先级关系,应正确使用括号,否则要发生错误。
如:AB + A ‾ \overline{A} AC
其对偶式为:(A + B) · ( A ‾ \overline{A} A + C) -
反演法则
由原函数求反函数,称为反演或求反。摩尔根定律是进行反演的重要工具。多次应用摩尔根定律,可以求出一个函数的反函数。
3.1.2 基本公式的应用
逻辑函数的形式是多种多样的,一个逻辑问题可以用多种形式的逻辑函数来表示,每一种函数对应一种逻辑电路。逻辑函数的表达形式通常分为五种:与或表达式、与非—与非表达式、与或非表达式、或与表达式、或非—或非表达式。
3.2逻辑函数的代数化简
逻辑函数的化简,在逻辑设计中十分重要的课题。化简的有 代数化简法 和 卡诺图法 两种。
3.2.1 逻辑函数与逻辑图
逻辑图与逻辑函数有直接关系。函数式越简单,实现该逻辑函数式所需要的的门数就越少,这样既可节省材料,且焊点少,又可提高电路的可靠性。
3.2.2 逻辑函数的化简原则
逻辑函数通常遵循以下几条原则:
- 逻辑电路所用的每最少;
- 各个门的输入端要少;
- 逻辑电路所用的级数要少;
- 逻辑电路能可靠地工作。
3.2.3与或逻辑函数的简化
- 应用吸收率(1)(AB + A B ‾ \overline{B} B = A)
- 应用吸收率(2)(3) (A + AB = A ; A+ A ‾ \overline{A} AB = A + B)
- 应用多余项定理(AB + A ‾ \overline{A} AC + BC = AB + A ‾ \overline{A} AC)
- 综合应用举例
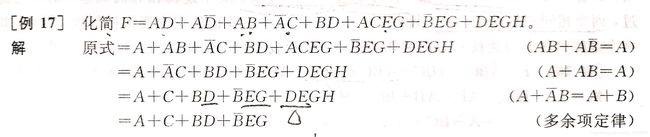
- 拆项法
- 添项法
3.3 卡诺图化简
图形化简逻辑函数是1952年由维奇(W.Veitch)首先提出来的,1953年卡诺(Kar-naugh)进行了更新系统、全面的阐述,故又称卡诺图法。
3.3.1 卡诺图化简的基本原理
逻辑相邻项:两个相同变量的逻辑项,只有一个变量取值不同,我们称它为逻辑相邻项。利用吸收率。
3.3.2 逻辑函数的标准式——最小项
- 最小项的标准式的定义
最小项标准式是以 ***“与或”***形式出现的标准式。
(1)最小项:对于一个 给定变量数组 的逻辑函数,所有变量参加 “与” 的项叫做最小项。在一个最小相中,每个变量只能以 原变量 或 反变量 出现一次。
(2)最小项标准式:全是由最小项组成的 “与或” 式,便是最小项的标准式(不一定由全部最小项组成。)
例如:F(A B C) = A ‾ \overline{A} A B ‾ \overline{B} B C ‾ \overline{C} C + A ‾ \overline{A} A B ‾ \overline{B} B C + A ‾ \overline{A} A B C ‾ \overline{C} C + A ‾ \overline{A} A B C + A B C
最小项标准式具有唯一性。任何逻辑函数的最小项标准式只有一个,它和逻辑函数的真值表有着严格的对应关系,而函数的一般式具有多样性。 - 由一般式获取最小项标准式
一般式转换最小项方法:
(1)代数法。对逻辑函数的一般式采用增项法。
(2)真值法。将原逻辑函数A、B、C取不同值组合起来,得其真值表,而该逻辑函数将是F=1对应的那些输入变量相或而成的。
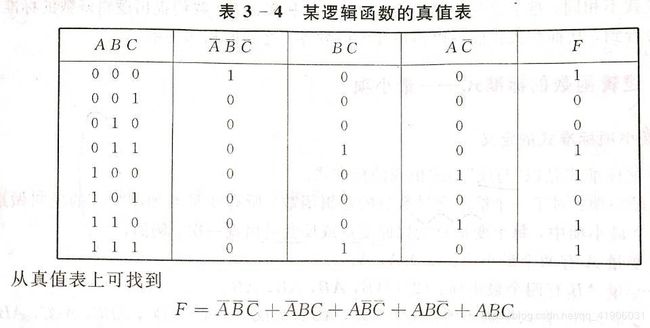
最小项编号:
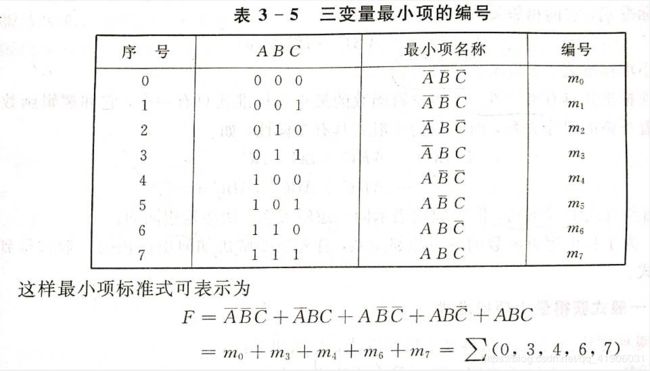
- 最小项的性质
(1)全部最小项的和为1;
(2)任意两个不同的最小项的积为0;
(3)n变量有2n项最小项,且对每一个最小项而言,有n个最小项与之相邻。
3.3.3 卡诺图结构
卡诺图结构特点是需要需要保证逻辑函数的 逻辑相邻关系,即图上的 何相邻关系。卡诺图上每一个小方格最小项。为保证上述相邻关系,每相邻放个的变量组合之间只允许一个变量值不同。为此卡诺图的变量标注采用 循环码。
4变量卡诺图:
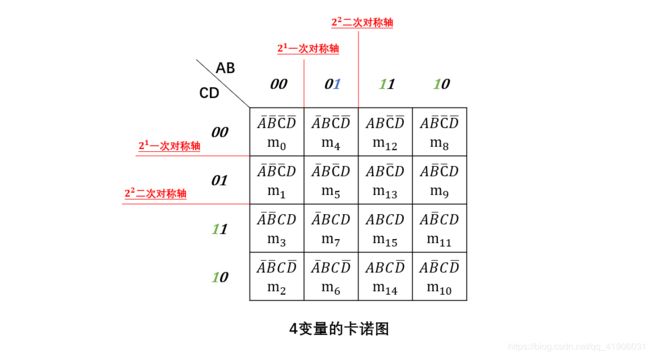
5变量卡诺图:
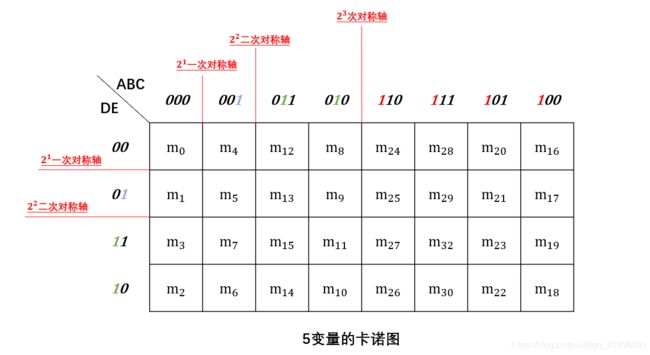
在卡诺图中若为n变量的卡诺图,则任意一个最小值有n个最小值与之相邻。例如5变量的卡诺图中的m7,与之相邻的最小量有m3、m5、m6、m15、m23。因为卡诺图是平面结构,从位置关系上开m7与m23并不是相邻关系,但是m7与m23是关于23三次对称轴对称关系,所以m7与m23是属于相邻关系。
2.3.4 逻辑函数的卡诺图表示法
逻辑函数由最小项组成,则可以直接用卡诺图对应的方格中填上1,其余填0。
例如:F = ABC + AB C ‾ \overline{C} C + A B ‾ \overline{B} BC + A ‾ \overline{A} A B ‾ \overline{B} BC = m7 + m6 + m5 + m1
用卡诺图表示为: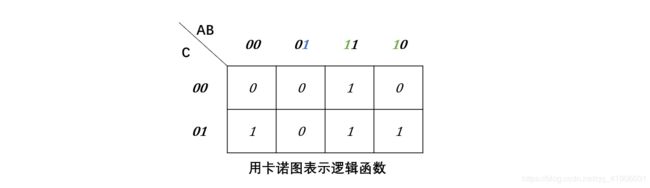
若逻辑函数不是有最小项组成,且包括其余项:
例如:F = B C ‾ \overline{C} C + C D ‾ \overline{D} D + B ‾ \overline{B} BCD + A ‾ \overline{A} A C ‾ \overline{C} CD + ABCD
用卡诺图表示方法,首先将各项分开以次用卡诺图表示,然后在合起来。
B C ‾ \overline{C} C:在B = 1,C = 0对应的方格(不管A,D)中填1,即m4、m5、m2、m13;
C D ‾ \overline{D} D:在C = 1,D = 0对应的方格(不管A,B)中填1,即m2、m6、m10、m14;
B ‾ \overline{B} BCD:在B = 0,C = 1,D = 1,对应的方格(不管A)中填1,即m3、m11;
A ‾ \overline{A} A C ‾ \overline{C} CD:在A = 0,C = 0,D = 1,对应的方格(不管B)中填1,即m1、m5;
ABCD:即m5。
即用卡诺图表示形式如下图:
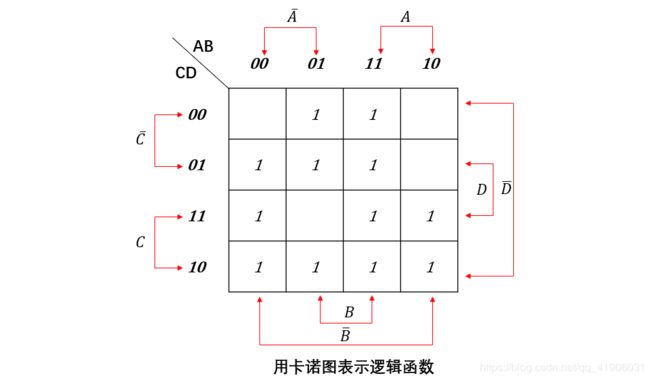
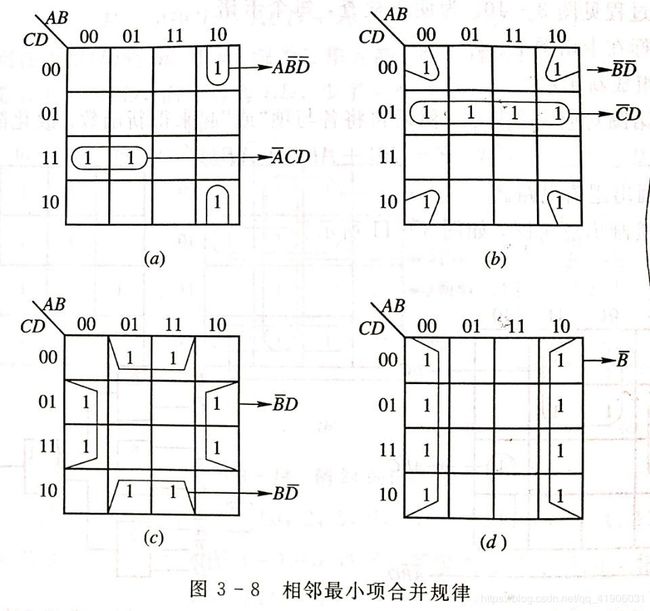
3.3.5 相邻项合并规律
- 两相邻项可合并为一项,消去一个取值不同的变量,保留相同变量,标注为1——原变量,0——反变量;
- 四相邻项可合并为一项,消去两个取值不同的变量,保留相同变量,标注为1——原变量,0——反变量;
- 八相邻项可合并为一项,消去三个取值不同的变量,保留相同变量,标注为1——原变量,0——反变量;
总结:合并的规律为2n个逻辑相邻项,不满足2n关系的最小或不组成方形不可合并,则2n个相邻最小项可消除n个不同的变量。
3.3.6
运用最小项标准式,在卡诺图上进行逻辑函数化简,得到的基本形式是 与或逻辑。其步骤如下:
- 将原始函数用卡诺图表示;
- 根据最小项合并规律画出卡诺图圈,圈住全部为 “1” 的方格;
- 将上述全部卡诺图圈的结果向 “或” 即得化简后的新函数;
- 有逻辑门电路,组成逻辑电路图。
根据最小项的合并规律我们知道,卡诺图圈越大,经化简消去的变量越多,结果越简单。每个卡诺图就是一个 “与” 项。显然,化简后看过全越少,电路越简单。还需要指出的是,如果卡诺圈的 “1” 方格均被卡诺圈圈过,则该卡诺圈是多余项,组成新的函数项就是多余项。函数化简时,这样的卡诺圈可以省略。为了避免圈的多余项,应保证每个卡诺圈内至少有一个 **“1”**方格未被别的卡诺圈圈过。

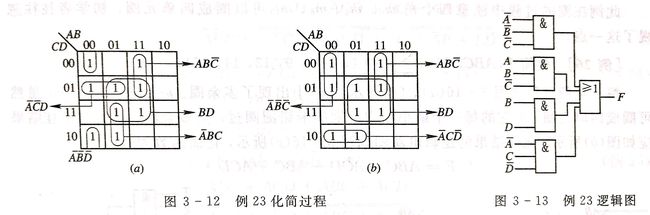
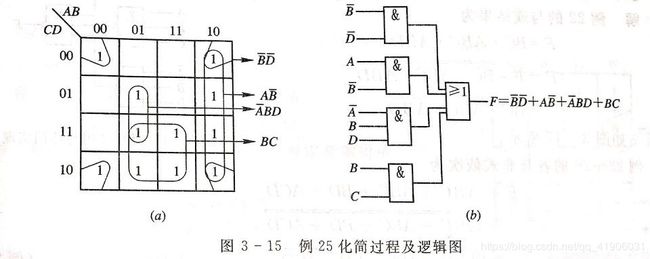

3.3.7其他逻辑函数式的化简
常用的有五种形式,与或式仅是其中一种。
- 与非逻辑形式
- 或与逻辑形式
- 或非逻辑形式
- 与或非逻辑形式
3.3.8无关项及其应用
逻辑问题分 完全描述 和 非完全描 述两种。
与函数无关的最小项称为最小项,有时又称为禁止项、约束项、任一项。
函数中只有部分最小项有关 ,而与另一些最小项无关,这下无关的最小项通常用 φ 或者 X 表示。
无关项的处理是任意的,可以认为是 “1” ,也可以认为是 “0” 。对于含有无关项的逻辑函数的化简,要考虑到无关项,当它对函数化简有利时,就认为它是 “1” ,反之则认为是 “0” 。
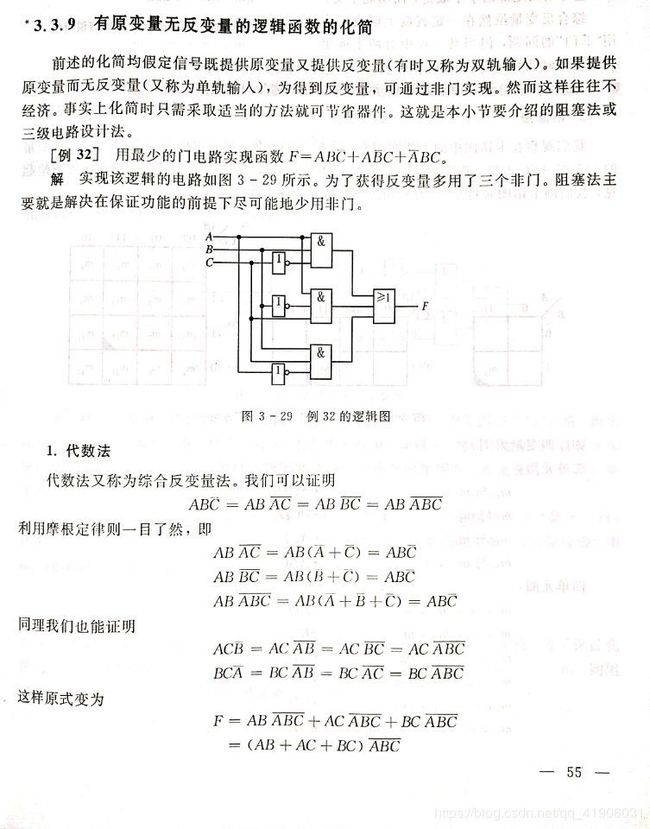
*3.3.9 有原变量无反变量的逻辑函数的化简
第四章 组合逻辑电路
数字电路可分为组合逻辑电路和时序电路两大类。组合逻辑电路即电路的输出线号是该时刻输入信号的函数,与该时刻以前的输入状态无关。这种电路 无记忆功能,无反馈回路 。
由于输入只有0、1两种状态,因此n个输入量有2n种输入状态的组合,若把每种输入状态组合下的输出状态列出来,就形成了描述逻辑电路的真值表。
在实际工作中,我们会碰到两种情况:逻辑 电路分析 和 逻辑电路设计 。
- 逻辑电路的分析
逻辑电路的分析,就是对已知的逻辑电路,用逻辑函数来描述,并以此列出它的真值表,确定其功能。在进行产品 仿制 和 维修 数字设备时,分析过程显然是十分重要的。同时,通过逻辑分析,还可以发现原设计产品的不足之处,然后加以改进。 - 逻辑电路的设计
逻辑电路设计又称为逻辑电路综合。其任务是,根据实际中提出的逻辑功能,设计出实现该逻辑功能的电路。