数据结构之线性表01(顺序表、单链表、静态链表 基础）
线性表是数据结构的一种，线性表中数据元素之间的关系是一对一的关系。除了第一个元素和最后一个元素之外，每一个元素有且只有一个前驱和一个后继，第一个元素没有前驱，最后一个元素没有后继。
线性表可以分为顺序存储和链式存储
- 顺序存储：顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素，称为线性表的顺序存储结构或顺序映像。
- 链式存储：用一组任意的存储单元存储线性表中的数据元素，称为线性表的链式存储结构。它的存储单元可以是连续的，也可以是不连续的。
线性表的基本操作
InitList(*L): //初始化操作，建立一个空的线性表L。
ListEmpty(L)://判断线性表是否为空表，若线性表为空，则返回ture，否则返回false。
ClearList(*L)://清空线性表。
GetElem(L,i,*e)://将线性表的第i个元素值返回给e。
LocateElem(L,e)://在线性表L中查找与给定值e相关的元素，如果查找成功，返回该元素表中序号表示成功；否则，返回0表示失败。
ListInsert(*L,i,e)://在线性表L中第i个元素位置插入新元素e。
ListDelete(*L,i,*e)://删除线性表L中第i个位置元素，并用e返回其值。
//数组data[]:线性表存储空间的存储位置
线性表的存储结构
获取线性表L的长度
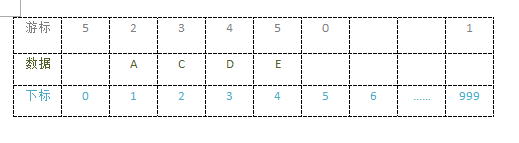
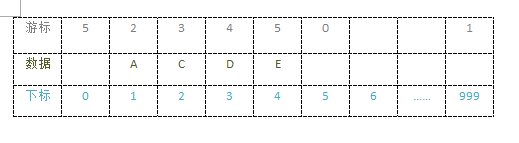
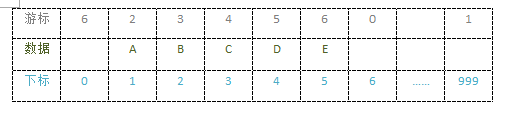
//静态链表中使用
#define Max 500 //定义数组的长度
int ListLength(StaticLinkList L )
{
int j = 0;
int i = L[MAX-1].cur; // cur指游标
while(i)
{
i = L[i].cor;
j++;
}
return j;
}
- 顺序存储结构
#define OK 1
#define TRUE 1
#define ERROR 0
#define FALSE 0
typedef int status1; //status 表示状态 Status i;类似于 int i;
//顺序存储初始化
status1 GetElem(SqList L, int i, ElemType *e)
{
if( L.length==0 || i<1 || i>L.length ) //线性表为空 或 i不存在
{
return ERROR;
}
*e = L.data[i - 1]; //将线性表L的第i个元素赋值给e
return OK;
}
- 链式存储结构
#define OK 1
#define TRUE 1
#define ERROR 0
#define FALSE 0
typedef struct2 Node
{
ElemType data； //数据域
struct2 Node* Next; //指针域
}Node；
typedef struct2 Node* LinkList;
//链式存储(单链表)初始化
struct2 GetElem( LinkList L, int i, ElemType *e )
{
int j;
LinkList P; //LinkList 相当于 Node*（指向一个节点的指针）
p = L->next;
j = 1;
while( p && j<i ) // p不为空 并且 i存在
{
P = P->next；
++j;
}
if(!p || j>i ) // p为空 或者 i不存在
{
return ERROR;
}
*e = P->data;
return OK;
}
- 静态存储结构
#define OK 1
#define TRUE 1
#define ERROR 0
#define FALSE 0
#define Max 500 //定义数组的长度
typedef struct3
{
ElemType data; // 数据
int cur ; // 游标
}Component, StaticLinkList[MAX];
//静态链表初始化
struct3 InitList(StaticLinkList space)
{
int i;
for( i=0; i<MAX-1; i++ )
{
space[i].cur = i + 1; // 游标指向下一个元素
}
space[MAX-1].cur = 0; //最后一个游标不存放元素 存放第一个元素的下标
return 0K;
}
线性表的插入操作
- 顺序存储
status1 ListInsert(SqList *L , int i, ElemType e)
{
int k;
if( L->length == MAXSIZE) // 顺序线性表以满
{
return ERROR;
}
if( i<1 || i>L-length+1) // 当i不在范围时
{
return REEOR;
}
if( i <=L->length ) //若插入位置不在表尾时
{
/* 将要插入位置以后的元素向后移动一位 */
for( k=L->length-1; k >= i-1; k-- )
{
L->data[k+1] = L->data[k];
}
}
l->data[i-1] = e; // 将新元素插入线性表
L->length++; //线性表长度+1
return OK;
}
- 链式存储(单链表)
struct2 ListInsert(LinkList *L, int i, ElemType e)
{
int j;
LinkList p, s; //相当于 Node *p， *s；
p = *L;
j = l;
while( p && j<i ) //若存在
{
p = p->next;
j++;
}
if( !p || j<i ) //若不存在
{
return ERROR;
}
S = (LinkList)malloc(sizeof(Node)); //在堆中临时创建大小为len(Node)的空间
s->data = e;
s->next = p->next;
p->next = s;
return OK;
}
- 静态链表
插入前：
过程：
插入后：
//01获取空闲分量的下标
int Malloc_SLL(StaticLinkList space)
{
int i = space[0].cur; //将下标为0的 游标 赋值给i
if( space[0].cur ) // 若存在（表示L有结束）
{
space[0].cur = space[i].cur; //将下标为i的 游标 赋值给下标为0的游标
}
return i; //新插入的元素存储在数组中下标为i的位置
}
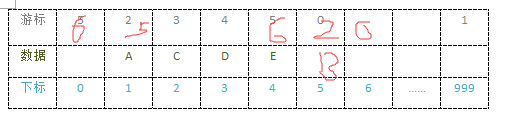
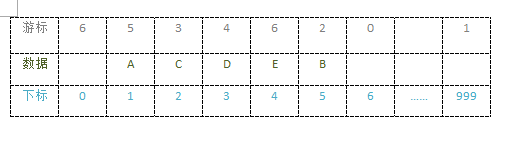
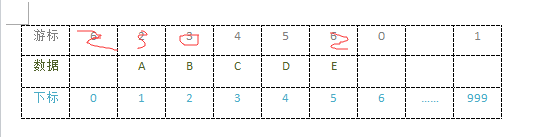
//02 在静态链表的第i个元素之前插入新的元素e
struct3 LinkList( StaticLinkList L, int i, ElemType e )
{
int j, k, l;
k = MAX-1; //数组最后一个元素的下标 //最后一个元素的游标指向第一个元素
if( i<1 || i>ListLength(L)+1 ) //若i不在数组中
{
return ERROR;
}
j =Malloc_SLL(L); //将数组中空闲的下标赋值给j
if( j )
{
L(j).data = e; //将e写入
for( l=1; l<=i-1; l++) //第i个元素之前（第i-1个元素之后）
{
k = L[k].cur; //第k个元素的游标赋值给k 找到下标为k的元素
}
L[j].cur = L[k].cor; //k的游标赋值给j的游标
L[k].cur = j; //j的下标存入k的游标
}
}
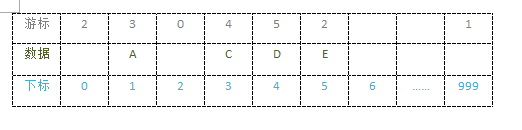
线性表的删除操作
- 顺序存储
stutus1 ListDelete(SqList *L, int i, ElemType *e)
{
int k;
if( L->length == 0 ) //链表为空
{
return ERROR;
}
if( i<1 || i>L->length ) //第i个元素小于1或大于线性表L的长度
{
return ERROR;
}
*e = L->data[i-1]; //将线性表L的第i个元素赋值给e
if( i < L->length ) // i存在
{
for( k=i, k<L->length; k++)
{
L->data[k-1] = L->data[k]; //将第k个元素用第k+1个元素覆盖
}
}
L->length--; //删除了一个元素所以线性表的长度-1
return OK;
}
- 链式存储(单链表)
2存在但没有指针指向其地址
struct2 ListDelete(LinkList *L, int i, ElemType *e)
{
int j;
LinkList p, q; //相当于 Node *p， *q；
p = *L;
j = 1;
while( p->next && j<i ) //p的下一个元素不为空 并且 在第i个元素之前
{
p = p->next;
++j;
}
if( !(p->next) || j>i ) //p的下一个元素若为空 或者 在第i个元素之后
{
return OK;
}
q = p->next; //将i的下一个元素赋值给q
p->next = q->next; // 相当于p->next = p->next->next;
//p的"下一个"元素此时变为随机数 相当于已经删除
*e = q->data;
free(q); //释放指针q
return 0k;
}
- 静态链表
删除前：
过程：
结果：
struct3 LinkDelete(StaticLinkList L, int i)
{
int j, k;
if(i<1 || i>ListLength(L)) //若不存在
{
return ERROR;
}
k = MAX-1;
for(j=1; j<=j-1; j++ )
{
k = L[k].cur; //第k个元素的游标赋值给k 找到下标为k的元素
}
j = L[k].cur ;
L[k].cur = L[j].cur;
Free_SLL(L, j);
return OK;
}