算法（一）排序算法（桶排序、冒泡排序、快速排序）

前言

这些一个系列的文章，主要是自己学习算法和数据结构的一些笔记整理。从最简单开始，一步步深入，都是自己学习过程中的领悟。对于程序猿而言，算法和数据结构就像一门强大的内功，练的过程中，会比较难，相对于武学招式，需要更多的理解能力和悟性，但是一旦练成，那就能变身强大的武林高手，纵横武林，不再是梦想。本系列武林秘籍主要来自于个人学习《啊哈！算法》《算法导论》这两个算法的入门级书籍。所以，高手就不喜勿喷啦。希望能对刚学算法的读者，有所帮助。个人水平有限，难免有错误，希望大家指正。好了，废话不多说，让我们开始学习神功吧。

正文

在学习编程语言的过程中，不管是c/c++、java、或者是python，其实都学习过排序，而我们神功的第一层，就是讲排序。其实排序正是高深武功的非常重要的基础，所以学会排序算法，是非常重要的。排序的算法有很多，这里我们主要讲讲三种排序桶排序、冒泡排序、快速排序。当然排序的算法还有很多，比如什么选择排序、插入排序等等。这里就暂时不做讨论了。

实际需求

对一个数组进行排序（真是简洁明了的说明呀），数组 {1,2,4,5,63,1,5,56,12,34,57,2,6,56,100}，这是一个班级里面学生的考试成绩的数组，现在需要我们对他进行排序

桶排序

所谓的桶排序其实就是，用桶来装出现过的数据，从而完成排序。

基本思想：

根据该数组中值的范围，定一个包括所有值的数组，比如一个班的学生的数学分数进行排序 那么就确定一个数组int[]  socre = new int [101];这样

就用socre数组的角标值标识分数，从0到100。然后遍历需要排序的数组，把 每个角标所存储的值，作为socre数组的角标，然后 对socre数组

当前角标的值进行++，从而确定了每个分数有多少人得了这个分数，然后再遍历socre数组，根据socre所存储的值的大小去确认 当前分数出现

的次数，这样就完成了对分数数组进行排序。

这里我们定义的包括所有值的数组socre，其实就是拿了一排桶过来，桶上面有编号0-100，然后把我们需要排序的小球数组，根据小球的编号（分数），分别放入这个桶里面，然后去数每一个桶里出现了多少个小球，从而完成了排序

基本实现：

private void bucketSort(){
        int[] a = {1,2,4,5,63,1,5,56,12,34,57,2,6,56,100};
        int[] aa = new int[100];
        for (int i = 0; i < aa.length; i++) {
            aa[i] = 0;//初始化桶
        }
        List aaa = new ArrayList<>();
        for (int i = 0; i < a.length; i++) {
            //这样就分别把这个数组中的数分到了对应的地方
            //根据分数，找到和分数相同的编号的桶，并且把小球放入桶内
            aa[a[i]] = aa[a[i]]+ 1;
        }
        for (int i = 0; i < aa.length; i++) {
            if (aa[i] != 0){
                for (int j = 0; j < aa[i]; j++) {
                    aaa.add(i+"");
                    Log.i("hero","------"+i);
                }
            }
        }
        Log.i("hero","--最终的排序是-----"+aaa.toString());
}

运行结果：

空间复杂度：

所谓的算法的空间复杂度，其实简单的理解就是该算法运行时，临时占用存储空间大小的度量。说白了，其实就是这个算法

运行的时候，会消耗多大的内存，那么桶排序的空间复杂度是什么样的呢？？从我们写的算法可以看出，其实该算法主要占用内存空

间的是原始数据数组和桶数组（List，aaa是便于输出观察的，不纳入计算），所以随着数据量的增加和数据内容的复杂，所需要的内存

越多。

时间复杂度：

所谓的算法的时间复杂度，其实就是算法运行所需的时间，我们近似的将每一行代码的执行时间看为相同，那么桶排序的

所需要的时间，就是第一行执行次数m，和第十一行执行次数n，简单的标示就是O(m+n)。桶排序其实是一种相当快速的排序方式。

总结：

我们现在已经学习了桶排序了，看吧，算法其实并没有你想象中的那么难，对不对？上面虽然我们完成了排序，但是如果我

们想要得到对应学生的排名，我们应该怎么做呢？上面其实只是对分数进行了排序，并没有和学生相对应起来，所以我们还需要其他

的排序算法。

冒泡排序

排序，其实就是按照数的大小顺序进行排列，比如正序就是把小的数放在左边，大的数放在右边。而冒泡排序做的事情就是将两 个相邻的数进行比较

和交换位置，从而达到排序的目的。

基本思想：

冒泡排序的基本思想就是一次循环，将一个数摆放在正确的位置上。

思路分析：

让我们以数组 {5,4,3,2,1}从小到大排序为例，来具体分析一下冒泡排序的具体思路

首先，冒泡的核心就是两个相邻的数进行比较，大的放右边，小的放左边

1、我们比较5,4，交换位置，得到4,5,3,2,1，那么下一步呢？既然是相邻位置比较，那么我们比较5.3

2、比较5,3, 并且交换，得到4,3,5,2,1

3、继续比较5,2，交换，得到4，3,2,5,1

4、比5，1，交换，得到4,3,2,1,5

上面四步，就完成了一次循环，我们得到了4,3,2,1,5

5、继续比较4,3，需要交换，得到3,4,2,1,5

6、比较4,2，需要交换，3,2,4,1,5

7、比较4,1，交换得到，，3,2,1,4,5

8、比较4,5，不需要交换

上面四次比较，我们又完成了一次排列，然后我们需要继续一次循环

这时候我们发现 好像没完没了了，那么什么时候该结束呢？也就是说我们应该进行多少次这样的比较循环呢，让我们来思考，其实一次循环，至少能确定一个数的位置，就是说，第一次循环，就可以把数组中最大的数，放在最右边的位置，第二次循环，就能将第二大的数放在右边第二个位置，也就是说，即使是最差的情况（完成逆序，和上面的例子一样），我们也最多通过5个这样的循环，其实就能完成排列了。

通过上面的分析，我们发现冒泡算法的核心，需要两个for循环，我们可以写出如下的代码

具体实现：

 private void bubbleSort(){
        int[] a = {5,4,3,2,1};
        for (int i = 0; i < a.length - 1; i++) {
            for (int j = 0; j < a.length - 1; j++){
               
                if (a[j] > a[j+1]){
                    int temp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = temp;
                }
            }
            Log.i("hero","---第--"+i+"---"+ Arrays.toString(a));
        }
        Log.i("hero","-----"+Arrays.toString(a));
    }

运行结果：

这样，我们就完成了冒泡排序了，但是，有没有什么可以优化的空间呢？其实我们上面已经说了，每一次内循环，就可以确定一个数的位置，那么，是不是第二次循环的时候，第8步，也就是4,5不需要比较了？所以我们优化后的算法如下

 private void bubbleSort() {
        int[] a = {5,4,3,2,1};

        for (int i = 0; i < a.length - 1; i++) {
            for (int j = 0; j < a.length - i - 1; j++) {
                //为什么要减i，因为每次都能确定一个末尾值，
                //第i次 就可以确认倒数第i个值，所以排了三次序之后
                //倒数的三个值都是确定的，所以不需要再对他们进行排序了
                //所以，可以减少排序次数
                //为什么要减1，因为循环里面是会j+1的，如果不减，会出现数组越界
                if (a[j] > a[j + 1]) {
                    int temp = a[j];
                    a[j] = a[j + 1];
                    a[j + 1] = temp;
                }
            }
            Log.i("hero", "---第--" + i + "-个循环--" + Arrays.toString(a));
        }
        Log.i("hero", "-----" + Arrays.toString(a));
    }

通过第二个循环，-i的操作，就完成了比较次数的优化，这样一来冒泡算法就解决了桶排序的空间复杂度的问题，

快速排序

虽然冒泡排序解决了桶排序的空间复杂度问题，但是实际上他的速度是远远比不上桶排序的，那么我们能不能基于冒泡算法，进行更多的优化呢？这就是我们要讲的快速排序。

思想核心：

快速排序主要思想是，通过“二分”思想，对数组中的数据进行跳跃式的排序。通过找一个基准数，每次排序完成，将比这个基准数大的都放在它的右边，比这个基准数小的数都放在它的左边。然后再分别对左右数组进行排序。

思路分析：

让我们以数组{5,1,9,26,2,4,5,7,52,21}升序排列，来进行分析

第一次排序：

首先，找一个"基准数"，比如5， 然后，先从右到左，找到第一个小于基准数的数，4，再从左到右，找到第一个大于基准数的数，9将它们进行交换，5，1,4,26,2,9,5,7,52,21

继续从右到左，寻找小于基准数的数，从左到右，寻找大于基准数的数，并交换，直到两个相遇，5,1,4,2,26,9,5,7,52,21    

现在右边找到的是2，左边到2的时候，还没有找到比基准数大的数，那么就将基准数和2进行交换  2,1,4,5,26,9,5,7,52,21 

这个时候，基准数左边的数，都是小于它的，右边的数都是大于等于它的。我们可以得到两个数列

2，1,4       26,9,5,7,52,21  然后分别对这两个数列进行上面顺序的排序

第一次排序结果：

基准数 5 结果：2,1,4,5,26,9,5,7,52,21  左边子数列 2,1,4  右边子数列  26,9,5,7,52,21

第二次排序：

比如 2,1,4  我们以2为基准数，右到左  找到1  左到右 到了1的角标也没找到，就将基准数和1进行交换

1，2,4    得到两个数列， 1   4  这两个数列都只有一个数，不需要排序了，左边数列的排序就完成了， 可以得到  1,2,4,5,26,9,5,7,52,21  

第二次排序结果：

基准数 2 结果：1,2,4,5,26,9,5,7,52,21  左边子数列 1  右边子数列 4

第三次排序：

左边数列 1 不需要排序

第三次排序结果：

基准数  1  结果：1,2,4,5,26,9,5,7,52,21  左边子数列 无   右边子数列 无

第四次排序：

右边数列 4  不需要排序

第四次排序结果：

基准数 4   结果：1,2,4,5,26,9,5,7,52,21  左边子数列 无   右边子数列  无

第五次排序：

再对第一次排序结果的右边的数列进行排序  26,9,5,7,52,21

以26为基准数 ， 右到左  21  左到右 52 交换21和52  得到26,9,5,7,21,52

它们还没相遇，继续以26为基准数，右到左，21   左到右 没有  交换 26和21 得到21,9,5,7,26,52

现在26左边的都小于它，右边的都大于它，

第五次排序结果：

基准数 26  结果：1,2,4,5,21,9,5,7,26,52   左边子数列 21,9,5,7  右边子数列 52

第六次排序：

对第五次排序的左边子数列进行排序

我们对21,9,5,7这个数列进行排序

以21为基准，右到左 7  左到右 没有 交换21 和7 得到7,9,5,21 基准数21右边没有 左边7,9，5数列都小于它

第六次排序结果：

基准数 21  结果：1,2,4,5,7,9,5,7,21,26,52  左边子数列 7,9,5  右边子数列 无

第七次排序：

对第六次排序的左边子数列进行排序

对7,9,5进行排序  以7为基准数 ，右到左 5  左到右 9 交换5和9  得到7,5,9

继续右到左 5  左到右 没有 交换基准数和5  得到5,7, 9 这时，基准数左边右边都排序完成 

第七次排序结果：

基准数  7 结果：1,2,4,5,5,7,9,21,26,52  左边子数列 5    右边子数列 9

第八次排序：

左边数列 5

第八次排序结果：

基准数 5  结果：1,2,4,5,5,7,9,21,26,52  左边子数列 无   右边子数列 无

第九次排序：

右边数列 9

第九次排序结果：

基准数 9  结果：1,2,4,5,5,7,9,21,26,52  左边子数列  无   右边子数列 无

第十次排序：

我们还有个第一次排序结果的右边子数列没有排序

基准数为26时，左边排序完成，剩下右边的数列 52 进行排序

第十次排序结果：

基准数 52 结果：1,2,4,5,5,7,9,21,26,52  左边子数列 无   右边子数列  无

此时，当所有排序都完成，得到了 1,2,4，5,5,7,9，21，26，52

快速排序之所以比冒泡排序快，是因为他的交换都是跳跃式的，而不像冒泡只能对相邻的进行排序。因此总的比较和交换的次数就少了，速度自然提高了。即使是最差的情况，也就是说还是相邻的进行交换，它的时间复杂度也是O（n * n）

算法实现：

private void fastSort(int left,int right){
    int temp;//保存的是基准数，用于基准数和左右相遇坐标点的交换
    int t;//用来辅助交换的数
    int i;
    int j;
    if (left > right){
        return;//说明该数列不需要排序
    }
    temp = a[left];//初始化基准数
    i = left;
    j = right;
    while (i != j){
        //如果两个角标还没有相遇
        //先从右到左，找第一个小于基准数的数
        while (a[j] >= temp && i < j){
            j--;
        }
        //从左到右，找第一个大于基准数的数
        while (a[i] <= temp && i < j){
            i++;
        }
        //现在找到的right和left角标，就进行交换
        if (i < j){
           t = a[i];
           a[i] = a[j];
            a[j] = t;
        }
    }
    //当i==j的时候，说明相遇了，需要将基准数和当前相遇坐标点的数进行交换。
    a[left] = a[i];
    a[i] = temp;
    // 到这里完成了一次基准数排序，现在需要递归对子数列进行排序
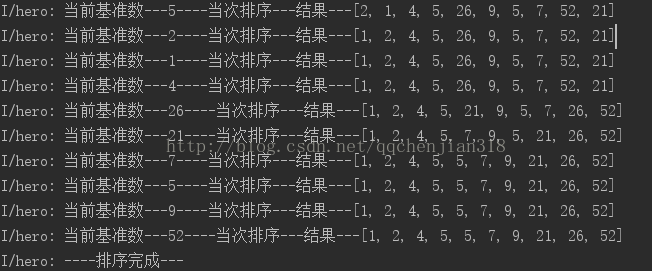
    Log.i("hero","当前基准数---"+temp+"----当次排序---结果---"+ Arrays.toString(a));
    fastSort(left,i-1);//对基准数左边子数列的进行排序
    fastSort(i+1,right);//对基准数右边子数列的进行排序
    return;
}

调用代码：

int[] a = {5,1,9,26,2,4,5,7,52,21};
 fastSort(0,a.length-1);

运行结果：

从运行结果可以看出，代码运行情况和我们分析的一模一样

时间复杂度：

         该算法的最差时间复杂度，即必须经过相邻的比较才能完成排序，跟冒泡排序是相同的都是O（n * n），但是他的平均时间复杂度是O（n * logn）。

快速排序和冒泡排序的一个对比

虽然我们已经说了快速排序是比冒泡排序要快一些的，那我们就来具体验证一下，初始化一个长度为1000的随机数组，数组里面存放范围在0 到100之间的一个随机数，然后比较两个算法谁执行速度快

运行结果：

从多次运行结果看来，其实快速排序确实要比冒泡排序快很多。

总结

本次学习就到这里了，我们学习了常见的三种排序方式，桶排序、冒泡排序、快速排序，对他们的思想和实现原理也进行了深入分析。最好自己动手，不看相关代码，去实现一遍，看看自己是否已经掌握了这几种排序方式。

算法这么神功，是不是其实并没有大家想象中的那么难呢？当然，这只是最最最基础的东西，加油，继续学习。

因个人水平有限，难免和不足之处，请多多指正。