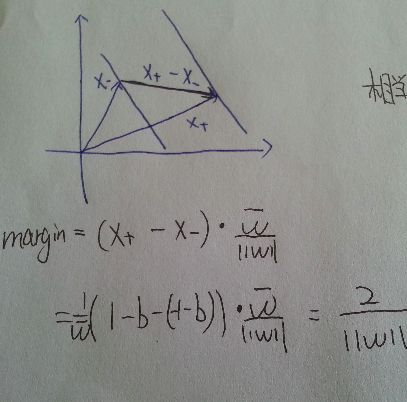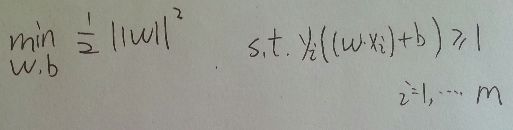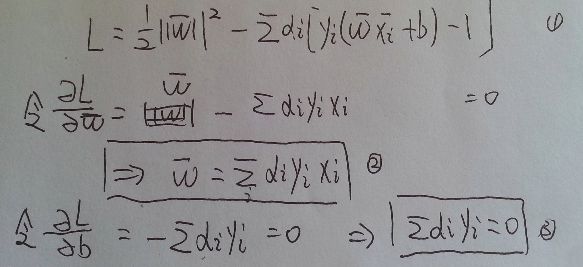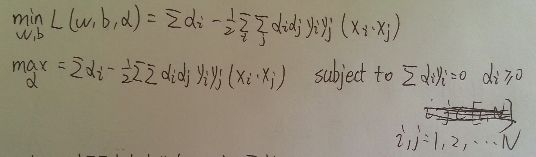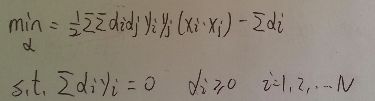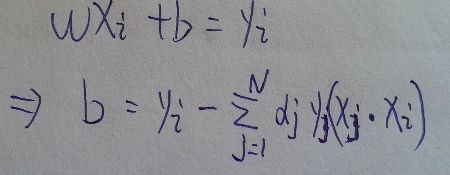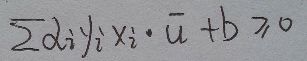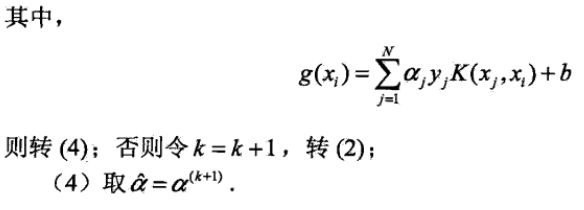SVM原理、公式推导、libsvm源码分析

恰好翻到了以前记的cs229的笔记, 其实也想了好久要不要跟风去推导公式, 写写就当是复习一下了

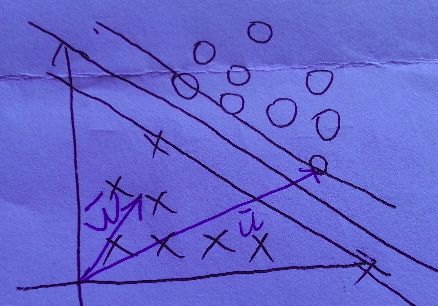
说到svm, 按套路就要先说说线性分类器, 如图, 在特征维数为2时, 可以用一条线将正负样本分离开来.当然了, 这条线可以有无数条, 假设我们训练得到了L2, 而L1是真正的那条直线, 对于新的测试样本(虚线的x), 显然, 用L2分类就会出现误分类. 也就是说, 线性分类器的效果并不怎么好, 但是很多都会把它作为概念的引入课程

后来92年有人提出了用一对平行的边界(boundry)来将正负样本(Pos/Neg example)分开, 其中中线确定了超平面(hyperplane)的位置, 如图. 

两个边界的距离, 我们称之为margin. 我们的目的是, 让这个margin尽可能的大, 最大边界上的正负样本, 我们称它们为支持向量(support vector). 所以如图, 对于垂直于超平面的单位向量w, 以及某个正样本的支持向量u, u在w上的投影便是右上的超平面到原点的距离, 即 wᐧu

可见正样本都是分布在wᐧu>= c 的区域(大于某个距离的区域), c是某个定常数. 令c = -b, 公式改写成

                 wᐧu+ b >= 0                           (decision rule)

所以对任意的正样本x, 我们令

                wᐧx + b >= 1

同理, 对于负样本x

                wᐧx + b <= - 1

相应的, 对于正负样本的标签, 分别是 y = 1 与 y=-1

这样不论对于正样本还是负样本,  我们都有

                y(wᐧx + b) >= 1

变形

                y(wᐧx + b) - 1>= 0

对于在边界上的正负样本, 有

                y(wᐧx + b) - 1 = 0

如图, 对于正负两个支持向量, 作差可以得到连接两个边界的一个向量, 再点乘前面的单位向量w, 得到了该向量在w方向上的投影, 便得到了margin的大小

到这里, 想想为什么要||w||的最小二乘方?而不是一次, 四次方?    ( cs229 Andrew的提问)

最小二乘法在很多假设下都有意义(make sense)  (Andrew的回答)

问题转化为如图形式, 这是一个凸二次规划问题(convex quadratic programming), 具体什么是凸二次规划问题, 可以参考<<统计学习方法>> 100页, 该页还有最大间隔存在的唯一性的证明

在这个形式下, 就是在y(wx+b)>=1的条件下最小化 ||w||的平方, 其中以w,b为变量

将它作为原始最优化问题, 应用拉格朗日对偶性(Lagrange Duality), 通过求对偶问题(dual problem)得到原始问题的最优解[1]

其实我也是从这里第一次接触二次规划的概念, 在没有不等式的条件下, 形式和我们高数学过的多元函数求简单极值一样, 即是求闭区域内连续有界多元函数的驻点或偏导不存在点

条件极值下, 就要引入拉格朗日乘子, 印象求解过程很麻烦

求对偶问题

如下构造拉格朗日方程 L(w,b,α),  引入了拉格朗日乘子α

α)

先对w, b求极小值, 再对α求极大值, 即

对α求最大值可以转化为对下式求最小值

以上

原始问题

转化为对偶问题(对第二行式子请自行脑补min(α)   )

---------------------------------------------------------------------------------------------------------------------------------------

对偶问题求解步骤

我们先根据上面的式子, 求出一组最优解 α , 后面说怎么求这个α

然后代入下面这里的 2式 求出w

因为任意支持向量满足, 所以b

实际上前面得到了w,        b = y - wx, 用任意一个支持向量去求b就可以

当我们求出了这样的一组α, w, b

代入最开始的决策函数decision rule 

                 wᐧu+ b >= 0                           (decision rule)

对于某个样本u, 当wᐧu+ b >= 0 , 我们可以判断它为正样本(实际上x也是向量, 这些样本自始至终都被当作向量对待)

回到上面的问题, 怎样求解α? 

之前我们分别先对w,b求偏导, 得到驻点, 注意这里并没有去判断是极大值点还是极小值点, 而是直接代入原方程求它对α的极大值. 

因为对b求偏导得到了等式条件3, 即所有αᐧ y之和为0, 这样我们可以减少对其中某个α的讨论. 

要想得到极值点就要分别对各个α进行求偏导, 得到驻点, 然后讨论每一个驻点以及边界点, 得到使该式子为min(对未变形的式子, 为max)的α值  

可能说的不太清楚, 大家可以看看[1]中的例题7.2, 让你自己求解一个支持向量机

------------

上面求解过程很麻烦, 样本容量很大时, 就需要优化了. 这一部分要用到SMO算法(因为书上[1]只讲到这一个, 其他的优化算法我也不知道).

首先要知道什么是KKT,关于KKT的ppt点这里, 这个ppt对我这个非数学专业的人比较好理解, 即便是对于没有学过多元函数求最值的人, 从求无条件极值, 到恒等式条件极值, 到等式/不等式条件极值循序渐进的介绍, 值得一看

所谓kkt条件, 就是最下面那三行式子

直观一点去对应

这不就是我前面推的那个式子么, 但是[1]基本上没提kkt是什么, wiki介绍的也不好, 这个地方写给和我一样曾有疑问的同学看.

smo的思路: 

1. 如果所有变量的解都满足KKT, 则该最优化问题的解得到

2. 如果不满足KKT, 则先选择两个变量, 固定其他变量, 对这两个变量构建二次规划问题

说句比较挨揍的话, 细节请看书吧, 后面的代码实现会再接触这些细节

图片来源:[1]

-------------------------------------------------------------------------------------------------------------------

libsvm代码分析:

看源码之前还要看看关于核函数和松弛变量的部分, 暂时先不讲了

先从简单的说起吧

1. decision function与predict函数

svm得到的decision function结构如下 ,  其中f.alpha = alpha, f.rho = si.rho  

alpha与rho都是训练得到的, rho实际上就是截距, 也就是决策函数 y = wᐧu+ b 中的 -b         

struct decision_function
{
	double *alpha;
	double rho;
};

得到判断函数后, 就可以拿他来predict

对应函数为

model=svm_load_model(argv[i+1]);
x = (struct svm_node *) malloc(max_nr_attr*sizeof(struct svm_node));
predict_label = svm_predict(model,x);
double svm_predict(const svm_model *model, const svm_node *x)
svm_predict_values(model, x, dec_values);
double svm_predict_values(const svm_model *model, const svm_node *x, double* dec_values);

我目前只关心线性svm分类器,即c_svc, 线性核

int nr_class = model->nr_class;     //类别数
int l = model->l;                              //支持向量总数

double *kvalue = Malloc(double,l);          //#define Malloc(type,n) (type *)malloc((n)*sizeof(type))
for(i=0;i    kvalue[i] = Kernel::k_function(x,model->SV[i],model->param);
// k_function按照kernel_type选择不同的返回值, 对线性核函数, 返回前两个前两个参数的点乘(Kernel::dot())
// model即我们训练得到的model
    int *start = Malloc(int,nr_class);              //分配类别数大小的内存
    start[0] = 0;                              //标记kvalue对于不同类的支持向量的起始位置, 因为kvalue是一整块内存

for(i=1;i    start[i] = start[i-1]+model->nSV[i-1];             //nSV[i]--第i+1类的支持向量数


int *vote = Malloc(int,nr_class);              //分配类别数大小的内存用来投票
for(i=0;i    vote[i] = 0;                                      //初始化投票数为0


int p=0;
for(i=0;i    for(int j=i+1;j    {
        double sum = 0;
        int si = start[i];                         //类别i对应的核函数得到的结果位置
        int sj = start[j];                         //类别j对应的核函数得到的结果位置
        int ci = model->nSV[i];            //类别i对应的支持向量数
        int cj = model->nSV[j];            // 类别j对应的支持向量数

        int k;
        double *coef1 = model->sv_coef[j-1];           //decision function的参数 [0,nr_class)
        double *coef2 = model->sv_coef[i];              //                                       [0,nr_class)
        for(k=0;k            sum += coef1[si+k] * kvalue[si+k];        
        for(k=0;k            sum += coef2[sj+k] * kvalue[sj+k];
        sum -= model->rho[p];
        dec_values[p] = sum;

------------------------------------------------------------------------------------------------------

上面这一段对应到opencv的代码是

                            const DecisionFunc& df = svm->decision_func[dfi];
                            sum = -df.rho;
                            int sv_count = svm->getSVCount(dfi);
                            const double* alpha = &svm->df_alpha[df.ofs];
                            const int* sv_index = &svm->df_index[df.ofs];
                            for( k = 0; k < sv_count; k++ )
                                sum += alpha[k]*buffer[sv_index[k]];


                            vote[sum > 0 ? i : j]++;

在我眼里opencv的可读性更好

----------------------------------------------------------------------------------------------------
        if(dec_values[p] > 0)
            ++vote[i];
        else
            ++vote[j];
        p++;
    }

    int vote_max_idx = 0;
    for(i=1;i        if(vote[i] > vote[vote_max_idx])
            vote_max_idx = i;

    free(kvalue);
    free(start);
    free(vote);
    return model->label[vote_max_idx];

}

有同学觉得不太明白, 不知道这张图够不够清楚, K(x,SV[i])代表 核函数K(Xi,Xj), 写的有点潦草请意会

--------------------------------------------------------------------------------------------------------------------------

关于svm_train.cpp, 实际上就是提取参数, 然后调用svm.h(svm.cpp)里面的train函数, 和svm_predict一样.

因为近期要准备出远门去面试, 需要好多准备, 这篇文章可能要拖延了, 实际上我是一边读代码一边写的, 我想好好写涉及到的算法、数据结构、内存管理, 对于我这样接触不到工程代码的人来说, 研究这种开源代码是很好的方式, 前提是得有时间, 最好能自己照着扒下来一份

                                                                                                       -------------2016. 9. 3  15:17

参考以及扩展阅读

[1] 李航,<<统计学习方法>>

[2]http://www2.imm.dtu.dk/courses/02711/lecture3.pdf

[3]Applications of Support Vector Machines for Pattern Recognition: A Survey

关于机器学习

公开课:

Andrew Ng(吴恩达) cs229   http://open.163.com/special/opencourse/machinelearning.html

Artificial Intelligence MIT6.034  https://www.youtube.com/watch?v=_PwhiWxHK8o&list=PLUl4u3cNGP63gFHB6xb-kVBiQHYe_4hSi&index=17

参考书 : PRML,MLAPP, <<统计学习方法>>

选择合适自己的资料就好, 讲的大多都是一个事情, 就看哪种表达方式适合你