伸展树(Splay tree)图解与实现
个人技术博客:http://blog.ztgreat.cn
一、伸展树
本文介绍了二叉查找树的一种改进数据结构–伸展树(Splay Tree)。它的主要特点是不会保证树一直是平衡的,但各种操作的平摊时间复杂度是O(log n),因而,从平摊复杂度上看,二叉查找树也是一种平衡二叉树。另外,相比于其他树状数据结构(如红黑树,AVL树等),伸展树的空间要求与编程复杂度要小得多。
伸展树的出发点是这样的:考虑到局部性原理(刚被访问的内容下次可能仍会被访问,查找次数多的内容可能下一次会被访问),为了使整个查找时间更小,被查频率高的那些节点应当经常处于靠近树根的位置。这样,很容易得想到以下这个方案:每次查找节点之后对树进行重构,把被查找的节点搬移到树根,这种自调整形式的二叉查找树就是伸展树。每次对伸展树进行操作后,它均会通过旋转的方法把被访问节点旋转到树根的位置。
为了将当前被访问节点旋转到树根,我们通常将节点自底向上旋转,直至该节点成为树根为止。“旋转”的巧妙之处就是在不打乱数列中数据大小关系(指中序遍历结果是全序的)情况下,所有基本操作的平摊复杂度仍为O(log n)。
在AVL树中我我们知道有4种旋转方式(实际是两种)RR型,LL型,RL型,LR型,如果不清楚AVL树旋转方式的可以参考平衡二叉树(AVL)图解与实现,个人觉还是说得很明白了,这里我们还是已图解的方式来讲解伸展树的操作,对伸展树的旋转操作中我沿用了AVL树中的部分名称,当然这个不是很严谨,主要是明白其中的原理,至于怎么称呼这个都是个人习惯而已。
首先给出伸展树的结构定义:
typedef struct SplayNode *Tree;
typedef int ElementType;
struct SplayNode
{
Tree parent; //该结点的父节点,方便操作
ElementType val; //结点值
Tree lchild;
Tree rchild;
SplayNode(int val=0) //默认构造函数
{
parent=NULL;
lchild=rchild=NULL;
this->val=val;
}
};
二、伸展树的旋转操作
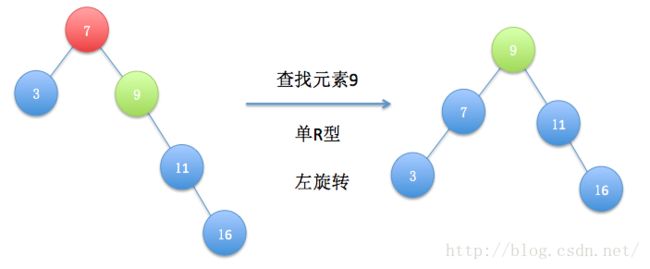
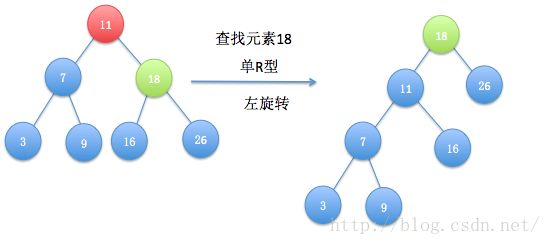
什么叫单R型呢,在上图中,我们查找的元素是9,其父节点是7,并且7是根结点,查找结点是其父节点的右孩子,而且把9变成根结点只需一次左旋转即可(即将9提升一层),这样的情况我们叫单R型,经过一次左旋转后结点9替代了原来的根结点7,变成新的根结点(注意这里因为图简单,9最终变成了根结点,在树复杂的情况,一般不会一次就变成了根结点,但肯定会变成原子树的根,这也就是程序中说的当前子树中的新根)。为了后面更加轻松,这里把单左旋代码贴出,可以对比图示和代码分析分析,便于理解
//单左旋操作
//参数:根,旋转结点(旋转中心)
//返回:当前子树中的新根
Tree left_single_rotate(Tree &root,Tree node)
{
if (node==NULL)
return NULL;
Tree parent=node->parent; //其父结点
Tree grandparent=parent->parent; //其祖父结点
parent->rchild=node->lchild; //设置其父节点的右孩子
if (node->lchild) //如果有左孩子则更新node结点左孩子的父节点信息
node->lchild->parent=parent;
node->lchild=parent; //更新node结点的左孩子信息
parent->parent=node; //更新原父节点的信息
node->parent=grandparent;
if (grandparent) //更新祖父孩子结点的信息
{
if (grandparent->lchild==parent)
grandparent->lchild=node;
else
grandparent->rchild=node;
}
else //不存在祖父节点,则原父节点为根,那么旋转后node为根
root=node;
return node;
}
(2)单L型
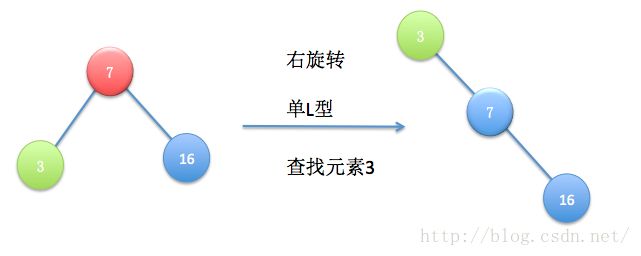
单L型和单R型是对称的,也就是说查找结点3是其父节点的左子树,并且其父节点是根结点,这样一次右旋转后3就是根结点了。
//单右旋操作
//参数:根,旋转结点(旋转中心)
//返回:当前子树中的新根
Tree right_single_rotate(Tree &root,Tree node)
{
if (node==NULL)
return NULL;
Tree parent,grandparent;
parent=node->parent;
grandparent=parent->parent;
parent->lchild=node->rchild;
if (node->rchild)
node->rchild->parent=parent;
node->rchild=parent;
parent->parent=node;
node->parent=grandparent;
if (grandparent)
{
if (grandparent->lchild==parent)
grandparent->lchild=node;
else
grandparent->rchild=node;
}
else
root=node;
return node;
}
(3)RR型
所谓RR型,简单点说就是两次R型,两次左旋转,这种情况是查找结点有父节点,同时也有祖父结点,并且三则在同右侧,这种就是RR型,针对这种情况,先把查找结点的父节点旋转一次,即提升一层,然后再以查找结点再次旋转,这样查找结点就到了根结点了,都是左旋转,只是旋转对象不一样罢了。
//两次单左旋操作
//参数:根,最后将变成子树根结点的结点
void left_double_rotate(Tree &root,Tree node)
{
left_single_rotate(root,node->parent);
left_single_rotate(root,node);
}
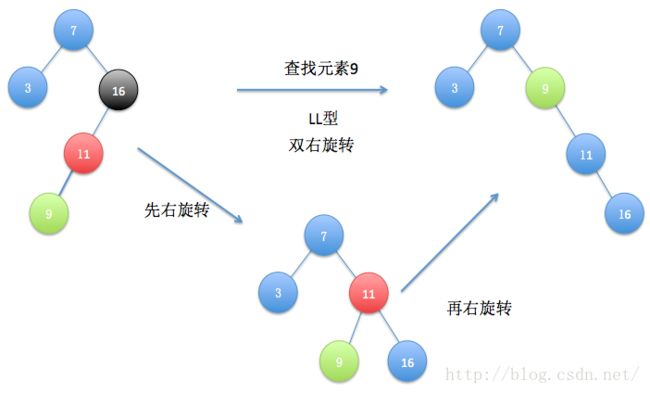
(4)LL型
//两次单右旋操作
//参数:根,最后将变成子树根结点的结点
void right_double_rotate(Tree &root,Tree node)
{
right_single_rotate(root,node->parent); //先提升其父节点
right_single_rotate(root,node); //最后提升自己
}
LL型和RR型是对称的,经过一次双右旋结果如上图,但是这样就结束了吗?回想一下,伸展树的旋转操作目的是干什么,不是为了把查找结点推送至树根么,是的,但是现在这种情况结点9还不是树根,但是这种情况不是我们前面讲过的单R型吗?所以再来次左旋就可以了,也就是下面这个样子:
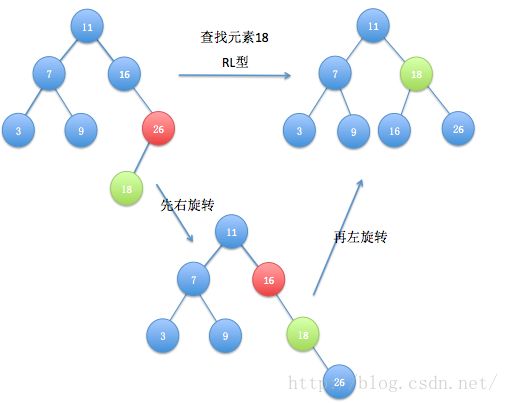
(5)RL型
//双旋操作(RL型),于AVL树类似
//参数:根,最后将变成子树根结点的结点
void RL_rotate(Tree&root,Tree node)
{
right_single_rotate(root,node); //先右后左
left_single_rotate(root,node);
}
这个和AVL树中的RL是一样的,旋转完成后,还需要一步左旋:
OK,到位了。
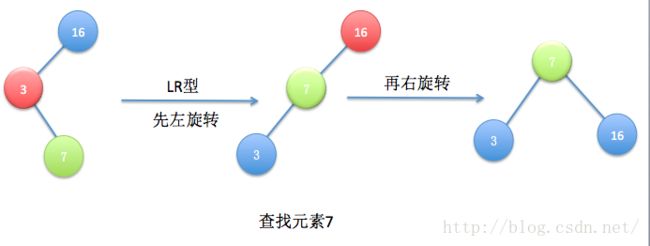
(6)LR型
//双旋操作(LR型),于AVL树类似
//参数:根,最后将变成子树根结点的结点
void LR_rotate(Tree &root,Tree node)
{
left_single_rotate(root,node); //先左
right_single_rotate(root,node);//后右
}
OK,到这里伸展树的几种情况就介绍完了,怎么这么多旋转方式,其实大可不必这样,这个只是我学习的时候自己总结的,和网上的也打不相同,主要是自己理解了它的旋转方式后,就好了,至于命名这些都影响不大,我这里把它们分为这几种的方式,主要是为了封装成函数,方便我的调用,这样逻辑更清楚一下,自己懂了以后就可以根据自己理解来组织代码了。
三、伸展树的操作
伸展树的操作和AVL树一样无非就是查,插,删,下面我们分别来介绍它们。
(1)先看看查找函数search:
//查找函数,带调整功能
//参数:根结点,需要查找的val
//返回:true or false
bool search(Tree &root,ElementType val)
{
Tree parent=NULL;
Tree *temp=NULL;
temp=search_val(root,val, parent);
if (*temp && *temp!=root)
{
SplayTree(root,*temp);
return true;
}
return false;
}
查找函数中里面有另一个具体的查找函数,我们先不管它,先梳理逻辑,首先我们通过内部的查找函数,查找值为val的结点,找到后返回结点给temp,如果查找成功,并且当前结点不是根结点,那么我们将进行树的调整,将结点temp推到树根,否则直接退出,这就是search的功能,简单明了。
//具体的查找函数
//参数:根,需要查找的val,父节点指针
//成功:返回其结点
//失败:返回其引用,方便后面的插入操作
Tree *search_val(Tree &root,ElementType val,Tree &parent)
{
if (root==NULL)
return &root;
if (root->val>val)
return search_val(root->lchild,val,parent=root);
else if(root->valrchild,val,parent=root);
return &root;
}
这里我们有必要介绍一下内部的查找函数,因为这是一个通用的接口,后面都会用到它,这个查找函数,如果查找成功则返回结点的引用,否则返回它该插入地方的引用,也就是其最后的parent的某个孩子,parent是查找成功或失败结点的父节点,也是引用类型。OK,这就是我们的查找函数,这里没有强化它的查找功能,只是方便我们后面的插入和删除工作。
(2)插入
//插入函数
//参数:根,需要插入的val
//返回:true or false
bool insert(Tree &root,ElementType val)
{
Tree *temp=NULL;
Tree parent=NULL;
//先查找,如果成功则无需插入,否则返回该结点的引用。
temp=search_val(root,val,parent);
if (*temp==NULL) //需要插入数据
{
Tree node=new SplayNode(val);
*temp=node; //因为是引用型,所以这里直接赋值,简化了很多了。
node->parent=parent; //设置父节点。
return true;
}
return false;
}
可以看到这个插入函数也是很短的,注意观察,里面有我们熟悉的东西,没错就是前面所讲的内部查找函数,这里对插入结点,我们先进行查找,如果查找成功就不进行插入,否则返回该插入地址的引用,这样我们直接让*temp=node,便完成了插入工作,简化了很多工作,然后设置父节点信息,插入成功。
(3)伸展
当我们查找一个val后,我们需要对树进行伸展,下面就是我们的伸展函数
//Splay调整操作
void SplayTree(Tree &root,Tree node)
{
while (root->lchild!=node && root->rchild!=node && root!=node) //当前结点不是根,或者不是其根的左右孩子,则根据情况进行旋转操作
up(root, node);
if (root->lchild==node) //当前结点为根的左孩子,只需进行一次单右旋
root=right_single_rotate(root, node);
else if(root->rchild==node) //当前结点为根的右孩子,只需进行一次单左旋
root=left_single_rotate(root, node);
}
可以看到,里面有个up函数,在这个函数外,还有单独的if判断结构,这两个if就是判断特殊情况的,也就是我们只需进行一个单旋便可以晋级为根结点的情况,这个很简单,结合一下图就可以看出来了。OK,看看我们的up函数
//根据情况,选择不同的旋转方式
void up(Tree &root,Tree node)
{
Tree parent,grandparent;
int i,j;
parent=node->parent;
grandparent=parent->parent;
i=grandparent->lchild==parent ? -1:1;
j=parent->lchild==node ?-1:1;
if (i==-1 && j==-1) //AVL树中的LL型
right_double_rotate(root, node);
else if(i==-1 && j==1) //AVL树中的LR型
LR_rotate(root, node);
else if(i==1 && j==-1) //AVL树中的RL型
RL_rotate(root, node);
else //AVL树中的RR型
left_double_rotate(root, node);
}
up顾名思义就是往上,也就是把查找结点往上推送,在这个函数里面我们判断了旋转类型,是LL型,还是RR型,还是LR型,亦或是RL型,然后再调用我们前面展示过的旋转函数。只需旋转函数最好结合图然后再看代码,这样很容易理解,不要只看代码。
到这里我们的查找和插入,以及伸展过程我们都展示了,这里很重要一个函数就是查找函数,还有就是几种旋转方式。
(4)删除
//删除操作
void remove(Tree &root,ElementType val)
{
Tree parent=NULL;
Tree *temp;
Tree *replace;
Tree replace2;
temp=search_val(root,val, parent); //先进行查找操作
if(*temp) //如果查找到了
{
if (*temp!=root) //判断是否是根结点,不是根结点,则需要调整至根结点
SplayTree(root, *temp);
//调至根结点或者本来就是根结点后进行删除,先查看是否有替代元素
if (root->rchild)
{
//有替代元素
replace=Find_Min(root->rchild); //找到替换元素
root->val=(*replace)->val; //替换
if ((*replace)->lchild==NULL) //左子树为空
{
replace2=*replace;
*replace=(*replace)->rchild; //重接其右孩子
delete replace2;
}
else if((*replace)->rchild==NULL) //右子树为空
{
replace2=*replace;
*replace=(*replace)->lchild; //重接其左孩子
delete replace2;
}
}
else
{
//无替代元素,则根直接移向左子树,不管左子树是否为空都可以处理
replace2=root;
root=root->lchild;
delete replace2;
}
}
}
在删除函数中,我们首先进行了查找,查找失败就退出,查找成功后,我们便把它推送到根结点,然后再用我们BST删除方式,找替代元素,这样化繁为简,只是这里统一采用引用方式,要简单很多。
下面是这是我们的熟悉的找替代元素的函数:
//操作当前子树的最小结点
//返回:其最小结点的引用
Tree *Find_Min(Tree &root)
{
if (root->lchild)
return Find_Min(root->lchild);
return &root;
}
OK,到这里我们的伸展树就介绍完了,在这里可以看到我们伸展树里面的函数和AVL树里面的函数差别很大,在AVL树里面,我们即采用了引用(部分),同时又可以通过返回值来设置,再加上手生,写得有点杂乱,这里的伸展树,我就统一采用引用方式,能不返回值就返回值,这样可以简化很多操作,加之伸展树本来就比AVL树简单,不同判断平衡因子,因此写起来就更加简单了。
下面就是我们总的代码:
#include
#include
#include
using namespace std;
typedef struct SplayNode *Tree;
typedef int ElementType;
struct SplayNode
{
Tree parent; //该结点的父节点,方便操作
ElementType val; //结点值
Tree lchild;
Tree rchild;
SplayNode(int val=0) //默认构造函数
{
parent=NULL;
lchild=rchild=NULL;
this->val=val;
}
};
bool search(Tree &,ElementType);
Tree *search_val(Tree&,ElementType,Tree&);
bool insert(Tree &,ElementType);
Tree left_single_rotate(Tree&,Tree);
Tree right_single_rotate(Tree &,Tree );
void LR_rotate(Tree&,Tree );
void RL_rotate(Tree&,Tree );
void right_double_rotate(Tree&,Tree );
void left_double_rotate(Tree&,Tree );
void SplayTree(Tree &,Tree);
void up(Tree &,Tree );
Tree *Find_Min(Tree &);
void remove(Tree &,ElementType);
//查找函数,带调整功能
//参数:根结点,需要查找的val
//返回:true or false
bool search(Tree &root,ElementType val)
{
Tree parent=NULL;
Tree *temp=NULL;
temp=search_val(root,val, parent);
if (*temp && *temp!=root)
{
SplayTree(root,*temp);
return true;
}
return false;
}
//具体的查找函数
//参数:根,需要查找的val,父节点指针
//成功:返回其结点
//失败:返回其引用,方便后面的插入操作
Tree *search_val(Tree &root,ElementType val,Tree &parent)
{
if (root==NULL)
return &root;
if (root->val>val)
return search_val(root->lchild,val,parent=root);
else if(root->valrchild,val,parent=root);
return &root;
}
//插入函数
//参数:根,需要插入的val
//返回:true or false
bool insert(Tree &root,ElementType val)
{
Tree *temp=NULL;
Tree parent=NULL;
//先查找,如果成功则无需插入,否则返回该结点的引用。
temp=search_val(root,val,parent);
if (*temp==NULL) //需要插入数据
{
Tree node=new SplayNode(val);
*temp=node; //因为是引用型,所以这里直接赋值,简化了很多了。
node->parent=parent; //设置父节点。
return true;
}
return false;
}
//单左旋操作
//参数:根,旋转结点(旋转中心)
//返回:当前子树中的新根
Tree left_single_rotate(Tree &root,Tree node)
{
if (node==NULL)
return NULL;
Tree parent=node->parent; //其父结点
Tree grandparent=parent->parent; //其祖父结点
parent->rchild=node->lchild; //设置其父节点的右孩子
if (node->lchild) //如果有左孩子则更新node结点左孩子的父节点信息
node->lchild->parent=parent;
node->lchild=parent; //更新node结点的左孩子信息
parent->parent=node; //更新原父节点的信息
node->parent=grandparent;
if (grandparent) //更新祖父孩子结点的信息
{
if (grandparent->lchild==parent)
grandparent->lchild=node;
else
grandparent->rchild=node;
}
else //不存在祖父节点,则原父节点为根,那么旋转后node为根
root=node;
return node;
}
//单右旋操作
//参数:根,旋转结点(旋转中心)
//返回:当前子树中的新根
Tree right_single_rotate(Tree &root,Tree node)
{
if (node==NULL)
return NULL;
Tree parent,grandparent;
parent=node->parent;
grandparent=parent->parent;
parent->lchild=node->rchild;
if (node->rchild)
node->rchild->parent=parent;
node->rchild=parent;
parent->parent=node;
node->parent=grandparent;
if (grandparent)
{
if (grandparent->lchild==parent)
grandparent->lchild=node;
else
grandparent->rchild=node;
}
else
root=node;
return node;
}
//双旋操作(LR型),于AVL树类似
//参数:根,最后将变成子树根结点的结点
void LR_rotate(Tree &root,Tree node)
{
left_single_rotate(root,node); //先左
right_single_rotate(root,node);//后右
}
//双旋操作(RL型),于AVL树类似
//参数:根,最后将变成子树根结点的结点
void RL_rotate(Tree&root,Tree node)
{
right_single_rotate(root,node); //先右后左
left_single_rotate(root,node);
}
//两次单右旋操作
//参数:根,最后将变成子树根结点的结点
void right_double_rotate(Tree &root,Tree node)
{
right_single_rotate(root,node->parent); //先提升其父节点
right_single_rotate(root,node); //最后提升自己
}
//两次单左旋操作
//参数:根,最后将变成子树根结点的结点
void left_double_rotate(Tree &root,Tree node)
{
left_single_rotate(root,node->parent);
left_single_rotate(root,node);
}
//Splay调整操作
void SplayTree(Tree &root,Tree node)
{
while (root->lchild!=node && root->rchild!=node && root!=node) //当前结点不是根,或者不是其根的左右孩子,则根据情况进行旋转操作
up(root, node);
if (root->lchild==node) //当前结点为根的左孩子,只需进行一次单右旋
root=right_single_rotate(root, node);
else if(root->rchild==node) //当前结点为根的右孩子,只需进行一次单左旋
root=left_single_rotate(root, node);
}
//根据情况,选择不同的旋转方式
void up(Tree &root,Tree node)
{
Tree parent,grandparent;
int i,j;
parent=node->parent;
grandparent=parent->parent;
i=grandparent->lchild==parent ? -1:1;
j=parent->lchild==node ?-1:1;
if (i==-1 && j==-1) //AVL树中的LL型
right_double_rotate(root, node);
else if(i==-1 && j==1) //AVL树中的LR型
LR_rotate(root, node);
else if(i==1 && j==-1) //AVL树中的RL型
RL_rotate(root, node);
else //AVL树中的RR型
left_double_rotate(root, node);
}
//操作当前子树的最小结点
//返回:其最小结点的引用
Tree *Find_Min(Tree &root)
{
if (root->lchild)
return Find_Min(root->lchild);
return &root;
}
//删除操作
void remove(Tree &root,ElementType val)
{
Tree parent=NULL;
Tree *temp;
Tree *replace;
Tree replace2;
temp=search_val(root,val, parent); //先进行查找操作
if(*temp) //如果查找到了
{
if (*temp!=root) //判断是否是根结点,不是根结点,则需要调整至根结点
SplayTree(root, *temp);
//调制根结点或者本来就是根结点后进行删除,先查看是否有替代元素
if (root->rchild)
{
//有替代元素
replace=Find_Min(root->rchild); //找到替换元素
root->val=(*replace)->val; //替换
if ((*replace)->lchild==NULL) //左子树为空
{
replace2=*replace;
*replace=(*replace)->rchild; //重接其右孩子
delete replace2;
}
else if((*replace)->rchild==NULL) //右子树为空
{
replace2=*replace;
*replace=(*replace)->lchild; //重接其左孩子
delete replace2;
}
}
else
{
//无替代元素,则根直接移向左子树,不管左子树是否为空都可以处理
replace2=root;
root=root->lchild;
delete replace2;
}
}
}
//前序
void PreOrder(Tree root)
{
if (root==NULL)
return;
printf("%d ",root->val);
PreOrder(root->lchild);
PreOrder(root->rchild);
}
//中序
void InOrder(Tree root)
{
if (root==NULL)
return;
InOrder(root->lchild);
printf("%d ",root->val);
InOrder(root->rchild);
}
int main()
{
Tree root=NULL;
insert(root, 11);
insert(root, 7);
insert(root, 18);
insert(root, 3);
insert(root, 9);
insert(root, 16);
insert(root, 26);
insert(root, 14);
insert(root, 15);
search(root,14);
printf("查找14:\n");
printf("前序:");
PreOrder(root);
printf("\n");
printf("中序:");
InOrder(root);
printf("\n");
// remove(root,16);
// remove(root,26);
// remove(root,11);
remove(root,16);
printf("删除16:\n");
printf("前序:");
PreOrder(root);
printf("\n");
printf("中序:");
InOrder(root);
printf("\n");
return 0;
}
程序我反复测试过,目前还没有发现问题,当然也是还存在bug,不管是代码还是思考过程,如果有问题,还希望各位不吝指教。感谢。
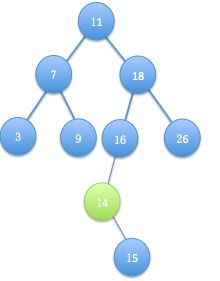
main函数中某测试数据的图:
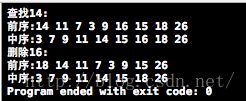
测试结果:
最后也许伸展树讲的比较简略,因为和AVL树有很大相识部分,可以参考一下:平衡二叉树AVL图解与实现
二叉搜索树的中的删除结点参考:二叉搜索树
如果对指针感到疑惑可以参看一下:C语言指针初探