LeetCode之树相关题目总结
文章目录
- 1.二叉树的最小深度【minimum-depth-of-binary-tree】
- 2.二叉树的最大深度【maximum-depth-of-binary-tree】
- 4 sum-root-to-leaf-numbers
- 5.Binary Tree Maximum Path Sum
- 6.populating-next-right-pointers-in-each-node
- 6.1 完全二叉树版本
- 6.2 任意二叉树版本
- 7 path-sum
- 7.1 是不是有到节点的路径的和等于给定的sum
- 7.2 哪些根到节点的路径的和等于给定的sum
1.二叉树的最小深度【minimum-depth-of-binary-tree】
题目:Given a binary tree, find its minimum depth.The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
思路一:该题目最直观的想法应该是,给定一个二叉树,直观看上去,哪一层最先叶子节点不全,其上一层就是最小的深度,也就是
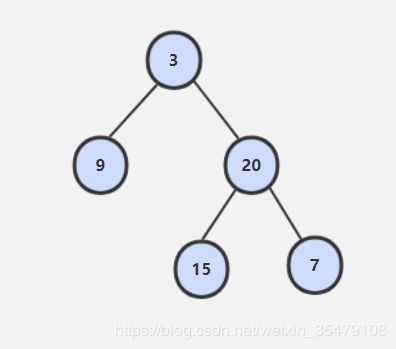
如上图,第三层最先开始缺少叶子节点构成完整二叉树的,所以最小的二叉树层次应该是上一层。这在二叉树里,严谨的语言应该是什么呢,等价转换成层序遍历的时候遇到的第一个叶子节点一定是深度最小的节点,如图中节点9。实现:需要用到树遍历中的层序优先遍历,从root层开始,按层次遍历,不需要遍历所有的节点。
class Solution {
public:
typedef TreeNode* tree;
int run(TreeNode *root) {
//采用广度优先搜索,或者层序遍历,找到的第一个叶节点的深度即是最浅。
if(! root) return 0;
queue<tree> qu;
tree last,now;
int level,size;
last = now = root;
level = 1;qu.push(root);
while(qu.size()){
now = qu.front();
qu.pop();
size = qu.size();
if(now->left) qu.push(now->left);
if(now->right) qu.push(now->right);
if(qu.size()-size == 0)break;
if(last == now){
level++;
if(qu.size()) last = qu.back();
}
}
return level;
}
};
思路二:就是常用的深度优先遍历,一条路走到黑。
- 运用递归,如果是空树返回0;
- 如果左子树为空,返回右子树的最小深度+1;【因为根节点有深度1】
- 如果右子树为空,返回左子树的最小深度+1;
- 如果左右子树都不为空,则取左右子树深度的较小值+1。
class Solution {
public:
int run(TreeNode *root) {
if(root == nullptr) return 0;
if(root->left == nullptr)
{
return run(root->right)+1;
}
if(root->right == nullptr)
{
return run(root->left)+1;
}
int leftDepth = run(root->left);
int rightDepth = run(root->right);
return (leftDepth < rightDepth)?(leftDepth+1):(rightDepth+1);
}
};
2.二叉树的最大深度【maximum-depth-of-binary-tree】
题目:
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
思路一:递归实现,与第一题一样,只不过递归返回的是左右子树层数较大的那一方。
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode *root) {
if(root == nullptr) return 0;
if(root->left == nullptr)
{
return maxDepth(root->right)+1;
}
if(root->right == nullptr)
{
return maxDepth(root->left)+1;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
return (leftDepth > rightDepth)?(leftDepth+1):(rightDepth+1);
}
};
思路二 层序遍历,遍历完每一层深度加1。什么时候遍历完一层呢?使用一个for循环,遍历上一次加入队列的节点。
这里区分一下栈和队列,栈是先进后出,队列先进先出,举例说明。
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode *root) {
if(root == nullptr) return 0;
TreeNode *node;
queue<TreeNode *> q;
q.push(root);
int depth = 0;
while(q.size())
{
int size = q.size();
TreeNode *temp;
for(int i = 0; i < size; i++)
{
temp = q.front();
q.pop();
if(temp->left != nullptr)
q.push(temp->left);
if(temp->right != nullptr)
q.push(temp->right);
}
depth++;
}
return depth;
}
};
4 sum-root-to-leaf-numbers
题目:Given a binary tree containing digits from0-9only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path1->2->3which represents the number123.
Find the total sum of all root-to-leaf numbers.
The root-to-leaf path1->2represents the number12.
The root-to-leaf path1->3represents the number13.
Return the sum = 12 + 13 =25.
思路:首先这个题目的求和方式很简单,节点数字的顺序排列也就是排在前面的数字以进制递增。然后,这个题目既然是关于树的题目,要求整个root-to-leaf的和就需要递归遍历二叉树,到叶结点之前,每一层的和都要乘以10,加上当前节点的值。
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int sumNumbers(TreeNode *root) {
int sum = 0;
if(!root) return sum;
return preorderSum(root,sum);
}
int preorderSum(TreeNode *root,int sum)
{
if(!root) return 0;
sum = sum*10 + root->val;
if(root->left == nullptr && root->right == nullptr)
return sum;
return preorderSum(root->left,sum)+preorderSum(root->right,sum);
}
};
5.Binary Tree Maximum Path Sum

讲解更详细一点
思路,摘自牛客:
首先我们分析一下对于指定某个节点为根时,最大的路径和有可能是哪些情况:
- 第一种是左子树的路径加上当前节点,
- 第二种是右子树的路径加上当前节点,
- 第三种是左右子树的路径加上当前节点(相当于一条横跨当前节点的路径),
- 第四种是只有自己的路径。
乍一看似乎以此为条件进行自下而上递归就行了,然而这四种情况只是用来计算以当前节点根的最大路径。如果当前节点上面还有节点,那它的父节点是不能累加第三种情况的,所以我们要计算两个最大值,一个是当前节点下最大路径和,另一个是如果要连接父节点时最大的路径和。我们用前者更新全局最大量,用后者返回递归值就行了。
针对该解题思路画了一个求解过程,解释如果当前节点上面还有节点,那它的父节点是不能累加第三种情况的。所以我们要计算两个最大值,一个是当前节点下最大路径和,另一个是如果要连接父节点时最大的路径和。
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int MaxVal = -128;
int maxPathSum(TreeNode *root) {
if(!root) return 0;
helper(root);
return MaxVal;
}
int helper(TreeNode *root)
{
if(!root) return 0;
int left = Max(0,helper(root->left));
int right = Max(0,helper(root->right));
MaxVal = Max(MaxVal,left+right+root->val);
return Max(left,right)+root->val;
}
int Max(int a,int b)
{
return (a>=b)?a:b;
}
};
6.populating-next-right-pointers-in-each-node
6.1 完全二叉树版本

简单来说,问题就是为每一个节点添加一个next,如果他右边有节点,就指向他右边的节点,如果没有节点,就为null。
实现思路:从根节点开始,找每一层的第一个节点,然后q->left->next = q->right; 这里q假设对应图中节点2,节点2是有next节点3的,因此需要将2-next->left赋给2->right->next。以上。
但是这是一个简化问题,考虑是一个完全二叉树,每一层最开始的节点都是p->left,下面进阶的题目是一个任意二叉树,需要判断每一层第一个节点。
/**
* Definition for binary tree with next pointer.
* struct TreeLinkNode {
* int val;
* TreeLinkNode *left, *right, *next;
* TreeLinkNode(int x) : val(x), left(NULL), right(NULL), next(NULL) {}
* };
*/
class Solution {
public:
void connect(TreeLinkNode *root) {
if(!root) return;
TreeLinkNode *p=root;
TreeLinkNode *q;
while(p->left)
{
q=p;
while(q)
{
q->left->next = q->right;
if(q->next)
{
q->right->next = q->next->left;
}
else
{
q->right->next = NULL;
}
q = q->next;
}
p = p->left;
}
}
};
6.2 任意二叉树版本
解题思路:使用一个flag标志,标识是不是每一层的第一个节点,每次循环默认节点->left是每一层的第一个节点,也就是flag标志是1,但是如果该节点没有做节点的话,就会判断该节点是不是有右节点,如果有就从这个节点开始标识next。
/**
* Definition for binary tree with next pointer.
* struct TreeLinkNode {
* int val;
* TreeLinkNode *left, *right, *next;
* TreeLinkNode(int x) : val(x), left(NULL), right(NULL), next(NULL) {}
* };
*/
class Solution {
public:
void connect(TreeLinkNode *root) {
TreeLinkNode *cur = root;
TreeLinkNode *temp;
int count = 1;
while (cur){
bool flag = true;
for (auto p = cur; p; p = p->next){
if (p->left){
if (flag){
cur = p->left;
flag = false;
temp = p->left;
}
else{
temp->next = p->left;
temp = temp->next;
}
}
if (p->right){
if (flag){//第一次进入该层
cur = p->right;
flag = false;
temp = p->right;
}
else{
temp->next = p->right;
temp = temp->next;
}
}
}
if (flag)//如果没进入for循环说明cur已经是最后一层
return;
}
}
};
7 path-sum
7.1 是不是有到节点的路径的和等于给定的sum

大家都是人才啊… 简单来说就是寻找从根到叶子节点有咩有一个路径的和等于给定的sum值,我一开始就想着计算每条路径的和,但是这个实际上只是返回是不是有这样的和,没有问具体路径,所以从最简单的开始,如果只有一个节点等于和返回true,如果不是的话就用sum-节点的值当成新的sum,递归调用左右节点的函数。
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode *root, int sum) {
if(!root) return false;
if(!root->left && !root->right && sum-root->val ==0)
return true;
return (hasPathSum(root->left,sum-root->val)) || (hasPathSum(root->right,sum-root->val));
}
};
7.2 哪些根到节点的路径的和等于给定的sum
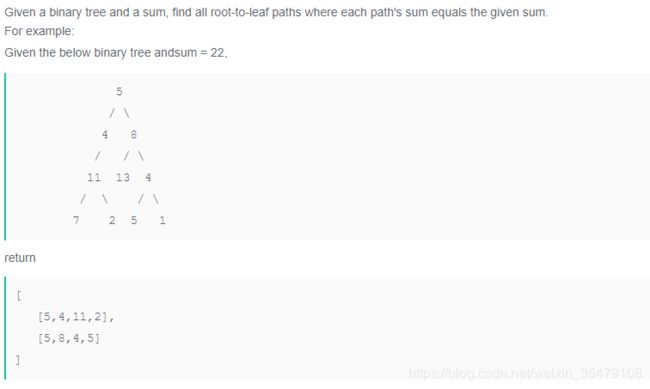
思路与上面一样,只是使用vector容器存储不同的路径即可。
有一个问题:写代码的时候,PathSearch函数中vector
举例来说:函数的参数传递有 :
- 按值传递,这时函数将为传递过来的参数创建一个副本,在函数运行的过程中,不会改变原来参数的值。这种情况下,考虑如果一个函数交换两个变量的值,就是不能实现的,因为函数中会交换两个副本的值,而对原来的参数没有任何影响。
- 如果要实现这个功能怎么办呢?还可以按指针传递参数,将要交换的两个数据的地址传递给函数,直接对地址的数值进行处理。
- 但是,按指针传递其实是容易出错的,因此还可以引入按引用传递。这时函数使用的也是原始数据,而不是其副本。
这个题目中,使用vector
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int> > pathSum(TreeNode *root, int sum) {
vector<vector<int>> Path;
vector<int> path;
if(!root) return Path;
PathSearch(root,sum,Path,path);
return Path;
}
void PathSearch(TreeNode *root,int sum,vector<vector<int>> &Path,vector<int> path)
{
if(!root) return;
path.push_back(root->val);
if(!root->left && !root->right && sum-root->val == 0)
Path.push_back(path);
PathSearch(root->left,sum-root->val,Path,path);
PathSearch(root->right,sum-root->val,Path,path);
}
};