【MATLAB】混合粒子群算法原理、代码及详解

1.算法

1.1.原理

\qquad 建议没接触过粒子群算法的朋友先看较为基础的全局粒子群算法原理及介绍，以下博文链接有详细的讲解、代码及其应用举例：
【Simulink】粒子群算法（PSO）整定PID参数（附代码和讲解）
\qquad 这里就介绍一下全局粒子群算法和混合粒子群算法的区别。全局粒子群算法（General PSO）将粒子速度矢量影响因子分为了三类：惯性因子、自身最优因子、社会因子。每个粒子的初速度定为0，即$v_0=0$，第$j$个粒子（$1\le j\le m$）的下一次迭代的速度$v^{(j)}$由以下三部分组成：
$$v^{(j)}=w\cdot v_0+c_1\cdot rand\cdot (P^{(j)}-X^{(j)})+c_2\cdot rand\cdot (P_G-X^{(j)})$$
注：rand是(0,1)的随机数，$v_0$代表上一次粒子的速度。
第一部分为自身惯性因子，因为下一次的迭代次数保留了上一次的速度信息；
第二个部分为自身最优因子，$P^{(j)}$为第$j$个因子在之前所有迭代次数中自适应度最高的位置，可以理解为历史上自身离最优解最近的位置。
第三部分为社会因子，$P_G$为种群在之前所有迭代次数中自适应度最高的位置，可以理解为历史上所有粒子离最优解最近的位置中的最近的一个。
\qquad 而混合粒子群算法（Hybrid PSO）与全局粒子群算法唯一的区别就是将社会因子分解为了两部分——局部社会因子和全局社会因子。即$$v^{(j)}=w\cdot v_0+c_1\cdot rand\cdot (P^{(j)}-X^{(j)})+c_2[q\cdot rand\cdot (P_G-X^{(j)})+(1-q)\cdot rand\cdot (P_L^{(j)}-X^{(j)})]$$
一般0＜q＜1,即两部分社会因子都为正。与上面不同的是$P_L^{(j)}$是第$j$个粒子的局部最优解的坐标。
\qquad 全局社会因子使得粒子的速度矢量有向（目前的）全局最优解趋向的趋势，而局部社会因子则使速度矢量包含向粒子的（目前的）局部最优解趋向的趋势。全局最优解好理解，局部最优解就是该粒子一定范围内粒子中的最优解，一般这个范围是固定的，而包含的粒子数量（如果为1，则是粒子本身）不确定。
\qquad 全局粒子群算法收敛速度快，但是对于多极值问题容易收敛到一个局部最优解；混合粒子群算法由于要计算局部最优解的原因，收敛速度慢，但可以很好地解决全局粒子群算法收敛到局部最优解的问题。

1.2.性能比较

\qquad 对粒子群算法感兴趣的朋友可以读一下面这两部分解释。

1.为什么全局粒子群算法容易收敛到局部最优解呢？
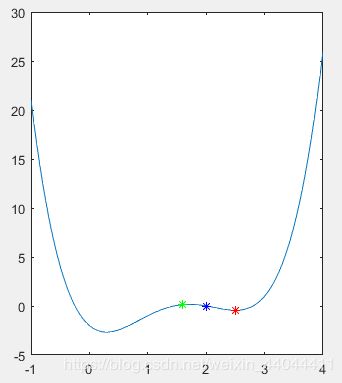
\qquad 我们不妨假设仅有3个粒子，目前有2个极小值点A和B，假设第一次迭代（位置随机，初速度为0），一个粒子a恰好就位于其中一个极小值点A附近，另2个粒子b和c彼此较近，但离B较远，函数值$f(A)<f(C)<f(B)$。初速度为0，惯性因子为0。又因为a就是当前全局最优点，自身最优因子也是本身（因为迭代次数为1），所以后两项都是0，a不会动。粒子b和c的历史最优因子就是它现在的位置，而社会因子使它向粒子a移动，并且每移动一次，它的自身最优因子都比上次的好，即不会对它的目前的速度造成任何影响。

\qquad 最终两个粒子都会收敛到极值点A。即使极值点B的目标函数值更小一些，但由于极值点A先被粒子群“找到”，因此就像一个极小值点黑洞一样，把所有的粒子都“吸”了过去。所以简单地来说，全局最优解就像一个吸引其他粒子的“黑洞”，如果在找到第二个“黑洞”之前所有粒子都被吸引到了第一个“黑洞”的周围，那就只能找到第一个局部最优解了。

1	2	3

2.那为什么混合粒子群算法就可以避免这个问题呢？
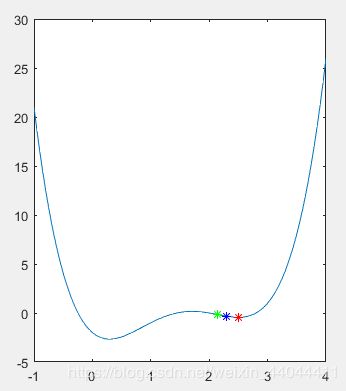
\qquad 我们不妨假设一个和上文一样的场景。目标函数只有2个极小值点A和B，第一次迭代，粒子a就位于A的附近，粒子b和c不位于B的附近，但彼此离得较近，离A较远。而且目标函数值都比a要大。初速度为0，因此三者的惯性因子为0。a的自身最优因子就是它本身，同时也是全局最优解，因此a不会动。而b、c的自身最优因子也是本身，然而全局社会最优因子是a，即二者都有向a偏移的趋势。

\qquad 现在考虑局部社会最优因子，b和c距离较小，会受到局部社会因子的影响；而二者都离a较远，不会受到a的影响（同样a也不会受到b和c的影响）。假设c的函数值比b小，因此b是c的局部最优解（同时也是它自身的）。在局部社会因子的作用下，b有向c移动的趋势；c和a均不受影响（c和a的局部最优解都是本身）。假设局部最优因子的权重合适，b应该向极小值B移动，c向a点移动。因为b有惯性因子，很可能在第二次迭代的过程中，离极小值B的距离会比c要短，满足$f(B)<f(C)<f(A)$。那么在接下来的几步迭代中，三者就会顺利收敛到极小值B附近，而不是更大的一个极小值A，进而找到全局最优解。

1	2	3	4

1.3.步骤

\qquad 步骤和全局粒子群算法基本一致，下面将不一样的步骤标红，看过全局粒子群算法那篇博文的读者可以重点关注一下。
【step0】确定参数维度$N$、参数范围（即每只鸟的初始位置），确定惯性系数$c_1,c_2,w$，确定种群规模m，迭代次数n以及局部因子作用半径$R$。

每个粒子的初始位置是随机的，设输入向量$x=(x_1,x_2,...,x_N{)}^T$必须满足参数范围限制为：
$$\{\begin{array}{l}{x}_{min}^{(1)}<x_1<x_{max}^{(1)}\\ x_{min}^{(2)}<x_2<x_{max}^{(2)}\\ ...\\ x_{min}^{(N)}<x_1<x_{max}^{(N)}\end{array}$$
记$X_{min}=(x_{min}^{(1)},x_{min}^{(2)},...x_{min}^{(N)}),X_{max}=(x_{max}^{(1)},x_{max}^{(2)},...x_{max}^{(N)})$
则输入向量$x$应满足$X_{min}<x<X_{max}$
【step1】计算每个粒子的速度
每个粒子的初速度定为0，即$v_0=0$，第$j$个粒子（$1\le j\le m$）的下一次迭代的速度$v^{(j)}$由三部分组成：
$$v^{(j)}=w\cdot v_0+c_1\cdot rand\cdot (P^{(j)}-X^{(j)})+c_2[q\cdot rand\cdot (P_G-X^{(j)})+(1-q)\cdot rand\cdot (P_L^{(j)}-X^{(j)})]$$

注：rand是(0,1)的随机数，$v_0$代表上一次粒子的速度。
第一部分为自身惯性因子，因为下一次的迭代次数保留了上一次的速度信息；
第二个部分为自身最优因子，$P^{(j)}$为第$j$个因子在之前所有迭代次数中自适应度最高的位置，可以理解为历史上自身离食物最近的位置。
第三部分为社会因子，由全局社会因子和局部社会因子组成。

$P_G$为全局最优解，是种群在之前所有迭代次数中自适应度最高的位置，可以理解为历史上所有粒子离食物最近的位置中的最近的一个。
一般情况下，取$w=1,c_1=c_2=2$，当种群规模较大时，可以让$w$的值随迭代次数减小以增加收敛速度。
$P_L^{(j)}$为局部最优解，每个粒子都有各自的局部最优解，可以理解为以该粒子为中心，$R$为半径的超球体内包含的所有粒子中自适应度最高的粒子的位置。q是全局社会因子的占比，比例越高局部社会因子所占的权重越小。$R$称为局部因子作用半径，和粒子分布平均密度有关。

【step2】按照step1的速度公式计算下一次的速度，并计算下一次的粒子位置。对于第$j$个粒子，第$k+1$次迭代（第$k+1$代）的位置$X_{k+1}^{(j)}$与第$k$次迭代的位置$X_K^{(j)}$与速度$v_k^{(k+1)}$关系为：
$$X_{k+1}^{(j)}=X_k^{(j)}+v_k^{(j+1)}\cdot dt$$
其中$dt$是仿真间隔，一般情况下可以取1，如果希望仿真得慢一点，搜索平滑一点，可以适当减小$dt$。
【step3】计算每个粒子的自适应度$F_{k+1}^{(j)}$，为了计算出step1公式中的$P^{(j)}、P_G$和$P_L^{(j)}$。为了方便起见，我们记前k次计算得到了的$P_G$为$P_G^{(k)}$，则第k+1次迭代中我们将适应度最高的粒子位置记为$P_G^{(k+1)}$，则最终的$P_G$为：
$$P_G=\{\begin{array}{l}{P}_G^{(k)}，F(P_G^{(k)})>F(P_G^{(k+1)})\\ P_G^{(k+1)}，F(P_G^{(k)})<F(P_G^{(k+1)})\end{array}$$
同样，我们记前k次计算得到的第$j$个粒子的位置为$P_k^{(j)}$，第k+1次计算得到的第$j$个粒子的位置为$P_{k+1}^{(j)}$，则最终的$P^{(j)}$为：
$$P^{(j)}=\{\begin{array}{l}{P}_k^{(j)}，F(P_k^{(j)})>F(P_{k+1}^{(j)})\\ P_{k+1}^{(j)}，F(P_k^{(j)})<F(P_{k+1}^{(j)})\end{array}$$
我们计第k次迭代的$P_L^{(j)}$为$P_{L_k}^{(j)}$，第$k$次迭代的第$i$粒子的位置为$P_k^{(i)}$则
$$P_{L_{k+1}}^{(j)}=avg[min(F(P_k^{(i)}))],||P_k^{(i)}-P_k^{(j)}||\le R$$
即所有距离第$j$个粒子不超过R的粒子中函数值最小的那个。
\qquad 注意$P_L^{(j)}$不需要保存为数组，也不需要和上次的值比较，它的值依赖于每次迭代粒子的位置，也会跟着来粒子位置分布的变化为变化。

【step4】更新每个粒子的信息。
由于我们在step2的位置迭代中已经更新过粒子的位置信息，在step1中的速度迭代中已经更新过粒子的速度信息，而在step3中又更新了每个粒子的历史最优位置$P^{(j)}$及种群最优位置$P_G$，因此实际上如果仅需要知道最优解的情况下我们不需要做这一步。
但如果需要作出参数随迭代次数的改变的图的话，每次迭代产生最优解$P_G^{(k)}$及最优适应度$F(P_G^{(k)})$需要用数组保存下来。

2.代码

2.1.源码及注释

\qquad 混合粒子群算法与全局粒子群算法的唯一区别就在一多出一个局部社会因子，计算局部社会因子就需要计算每个粒子为中心，R为半径的“局部”内自适应度最高的粒子。因此判断粒子与粒子间的距离成为了一大难题。将这部分代码写成并行形式，可以大大降低算法时间复杂度和空间复杂度。
\qquad 我们定义一个邻接矩阵
$$D=\left[\begin{array}{cccc}{d}_{11}& d_{12}& ...& d_{1n}\\ d_{21}& d_{22}& ...& d_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ d_{n1}& d_{n2}& ...& d_{nn}\end{array}\right]$$
其中$d_{ij}$代表第$i$个粒子距离第$j$个粒子的距离，$d_{ii}=0$。
每次迭代过程中都计算邻接矩阵$D$，计算第$j$粒子的局部社会因子时即参考$D$矩阵的第$j$行（或列）的数据即可。
计算邻接矩阵$D$的函数书写如下：(Distance_Matrix.m)

function DM=Distance_Matrix(X)
m=size(X,2);%维数
n=size(X,1);%样本数
DM=zeros(n,n);%距离矩阵
for t=1:m
    Dif=ones(n,1)*X(t,:)-X;%坐标差矩阵
    Dis=sum(Dif.^2,2);%第t个样本距离其他所有样本的距离（矩阵）
    DM(t,:)=Dis;
end

注意，这里X是样本矩阵，样本是以行向量的形式组成矩阵的。

主程序代码如下所示：(Hybrid_POS.m)

function [Pg,fmin]=Hybrid_PSO(f,dimension,n,m,xmax,xmin,vmax,vmin,R,p)
%混合粒子群算法,f为目标函数,dimension为维度,n为代数,m为种群规模
%位置限幅为[xmin,xmax]，速度限幅为[vmin,vmax]
%R为局部粒子群算法作用范围
%p为局部粒子群占的比重（Max=1）
% 以下四行为位置限幅和速度限幅，对应的四个参数均为行向量
    Xmax=ones(m,1)*xmax;
    Xmin=ones(m,1)*xmin;
    Vmax=ones(m,1)*vmax;
    Vmin=ones(m,1)*vmin;
    Savef=zeros(n+1,1);%记录自适应度F的数组
%   SaveData=zeros(m,dimension,10);%记录11代种群的位置，只需结果时不需要此数组
    w=1;c1=2;c2=2;%速度惯性系数
    dt=0.3;%位移仿真间隔
    v=zeros(m,dimension);%初始速度为0
    X=(Xmax-Xmin).*rand(m,dimension)+Xmin;%初始位置满足(-xmax,xmax)内均匀分布
    P=X;%P为每个粒子每代的最优位置
    DM=Distance_Matrix(X);%距离矩阵
    Local_Pg=zeros(m,dimension);%局部最优解矩阵
    last_f=f(X);
    [fmin,min_i]=min(last_f);%Pg为所有代中的最优位置 
    Pg=X(min_i,:);%获取这个最优位置的坐标
    Savef(1)=fmin;
    for i=1:m
        XR_i=find(DM(i,:)<R);
        [~,min_i]=min(last_f(XR_i));%按行筛选小于R的点
        Local_Pg(i,:)=X(XR_i(min_i),:);%局部最优解的坐标
    end
    N=0;
    for i=1:n
        v=w*v+c1*rand*(P-X)+c2*rand*((1-p)*(ones(m,1)*Pg-X)+p*(Local_Pg-X));
        v=(v>Vmax).*Vmax+(v>=Vmin & v<=Vmax).*v+(v<Vmin).*Vmin;
        X=X+v*dt;
        X=(X>Xmax).*Xmax+(X>=Xmin & X<=Xmax).*X+(X<Xmin).*Xmin;
        new_f=f(X);%新的目标函数值
        update_j=find(new_f<last_f);
        P(update_j,:)=X(update_j,:);%修正每个粒子的历史最优值
        [new_fmin,min_i]=min(new_f);
        new_Pg=X(min_i,:);
        Pg=(new_fmin<fmin)*new_Pg+(new_fmin>=fmin)*Pg;
        last_f=new_f;%保存当前的函数值
        fmin=min(new_fmin,fmin);%更新函数最小值
         Savef(i)=fmin;
         if mod(i,floor(n/10))==0%每10代记录一次种群参数
             N=N+1;
         %   SaveData(:,:,N)=X;
         end
        w=w-i/n*0.8*w;
    end
%     for j=1:10
%         figure(j)
%         plot(SaveData(:,1,j),SaveData(:,2,j),'o');
%         xlim([xmin(1),xmax(1)])
%         ylim([xmin(2),xmax(2)])
%         axis tight
%     end
    figure
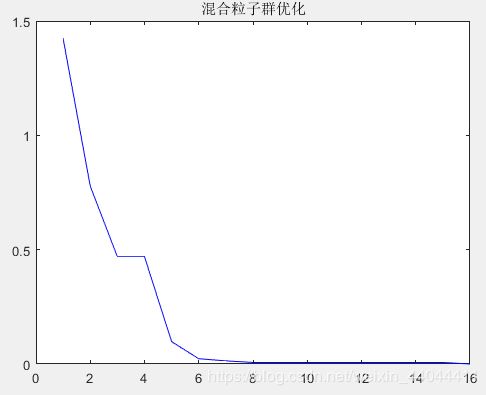
    plot(Savef','b-')
    title('混合粒子群优化')
    disp(Pg)
    disp(fmin)
end

注：代码注释部分是绘制数次迭代粒子分布位置，要解除需要一起解除（Ctlr+T）,否则会报错！

2.2.执行与效果

\qquad 我们首先来尝试使用RosenBrock函数（香蕉函数）对其进行试验。香蕉函数的极小值点为(1,1)，极小值为0。书写为匿名函数如下：

>> f=@(x)((1-x(:,1)).^2+100*(x(:,2)-x(:,1).^2).^2);

注：这里的冒号不可以省略，因为是样本为多维行向量组成的矩阵，所以函数也应返回同维向量而不是一个值。

我们设定一个稍大的范围，速度限幅设置为位置限幅约1/3的大小，局部社会因子取0.15，局部社会因子影响半径R取位置限幅的1/6。仿真命令及结果如下：

>> [Pg,fmin]=Hybrid_PSO(f,2,25,200,[10,10],[-10,-10],[3,3],[-3,-3],3,0.15)
    0.9731    0.9480

   8.2839e-04


Pg =

    0.9731    0.9480


fmin =

   8.2839e-04

目标函数的下降趋势如下：

粒子群的变化趋势如下图：

①	②	③
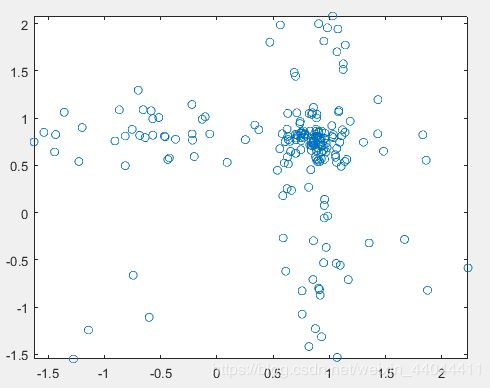④	⑤	⑥

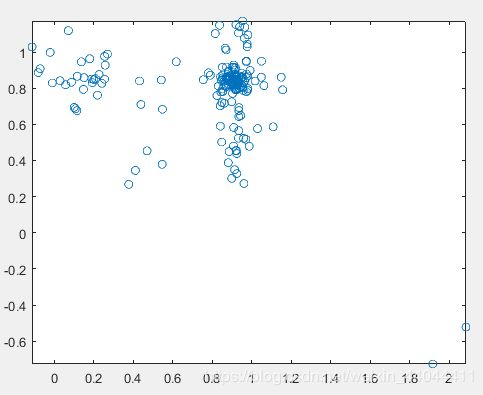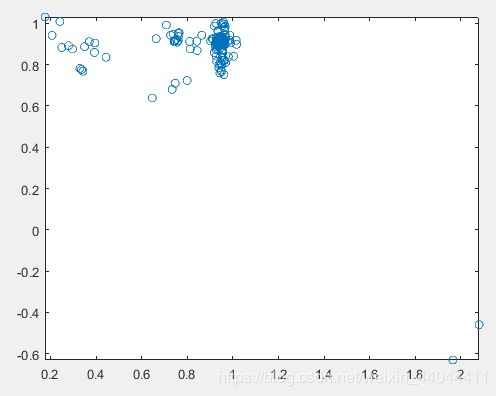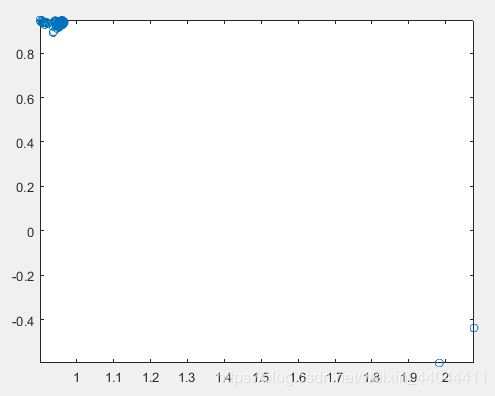可以发现粒子群算法顺利收敛到了(1,1)附近。

2.3.理解与进阶

\qquad 反问读者一个问题，如何提高混合粒子群算法(Hybrid PSO)的精度。肯定有人会说增加迭代次数n或者扩大种群规模m，除此之外，还有一个简单易行的方法，即在第一次结果的基础上进行第二次仿真，并把范围设置在第一次结果的附近，大大减小位置限幅和速度限幅的数值，仿真精度自然会提高。
\qquad 重新设置位置限幅为[0,2]，速度限幅为[-0.3,0.3]，R=0.3,再次仿真：

>> [Pg,fmin]=Hybrid_PSO(f,2,25,200,[2,2],[0,0],[0.3,0.3],[-0.3,-0.3],0.3,0.15)
    1.0009    1.0014

   9.9527e-06


Pg =

    1.0009    1.0014


fmin =

   9.9527e-06

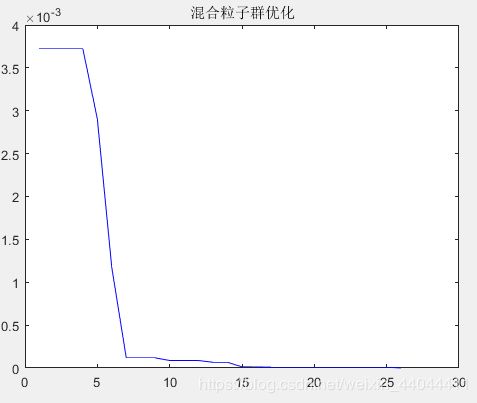
\qquad 可以发现二次仿真后最优解更加接近于(1,1)，极小值也大大缩小（缩小2个数量级）。读者可以思考如何修改代码以实现一次仿真就能代替二次仿真的效果。
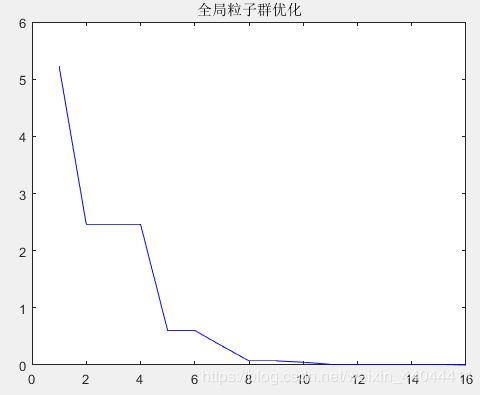
\qquad 混合粒子群算法在单极值的，或者极值不密集的解析函数上仿真与全局粒子群算法效果相差无几，将其参数$\rho$设为0，即为全局粒子群算法（但别以为这样可以提高运算速度）。我看看仿真结果的对比：

混合粒子群	全局粒子群
$\rho =0.15$	$\rho =0$
$[x_{min},x_{max}]=[-10,10]$	$[x_{min},x_{max}]=[-10,10]$
$[v_{min},v_{max}]=[-3,3]$	$[x_{min},x_{max}]=[-10,10]$
R=3	/
$x^{\ast }=(1.0809,1.1701)$	$x^{\ast }=(1.1044,1.2174)$
$f_{min}=0.0069$	$f_{min}=0.0115$

\qquad 但在优化类似神经网络、simulink函数等无解析式复杂函数时，混合粒子群求得更小极值的可能性更大（注意，粒子群每次仿真结果不一样，求得最优解只是一个概率收敛问题）。

希望本文对您有帮助，谢谢阅读！