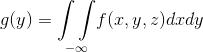贝叶斯网络(BN)的理解

贝叶斯网络：用点表示事件的条件概率，用边表示事件依赖关系的有向无环图（DAG）。

1.在贝叶斯往来中描述概率的方式是每个节点上的条件概率分布（CPD）;

2.贝叶斯网络的实质是对联合概率的描述。

事件状态	可枚举值	二项分布or多项分布
	连续变量	连续变量离散化后进行多项式分布
		在CPD中引入连续分布，如高斯分布N()

以典型贝叶斯问题为例：天气影响小林与女朋友当晚是否会有电话、是否会见面；当晚见面与否会影响是否会有电话的概率；女友在建模或者电话中都有肯问小林要礼物；是否索要礼物不与天气直接产生关系，但实际通过另两个结点有间接关系。其中的CPD和DAG如下所示：

事件abcd皆为可枚举值，其中每个节点的状态只有两种，于是概率采用二项分布 。假设天气情况分为晴阴雨雪四种，见面分为不见面、校内见面、校外见面，那么可能见面事件为多项式分布，CPD如下所示：

条件a（天气）	P(b=0)	P(b=1)	P(b=2)
0（晴）	0.6	0.2	0.2
1（阴）	0.2	0.3	0.5
2（雨）	0.1	0.5	0.4
3（雪）	0.3	0.7	0

假如礼物金额为连续变量，引入高斯分布：

条件b(见面)	条件c（电话）	P(d)
0	0
0	1
1	0
1	1

3.联合/边缘/条件概率换算

a.联合概率分布：P(a,b,c,...,n)，其中a,b,c,...,n为系统中的所有变量；

b.边缘概率分布：边缘概率的表达方式与联合概率一样，区别是通过边缘概率查询概率时只需给出系统中的部分变量，比如：g(a,b),g(b,d,g,n),g(b)......；

c.条件概率分布：P(a,b|i=?,j=?)表示在已知某些变量(i,j)的的情况下求另一些变量(a,b)给定值的概率；

d.用联合分布求边缘分布：已知联合概率分布函数f(x,y,z)，求边缘分布g(y)

             

对于离散变量，也就是

          

e.用联合概率分布求条件概率分布

类似：根据小林与女友是否有过电话，问天气如何，

           

假设有电话为1，那么P(x|y=1)就是小林与女友有过电话，问天气如何。

f.用条件概率和边缘概率求联合概率分布：P(x,y)=P(x|y)P(y)

根据链式法则：P(a,b,c,d)=P(a)P(b|a)P(c|a,b)P(d|b,c)

---

 变量消元：

---

网络构建（三步）：1.确定领域中有哪些是重要的变量以及其分布；

                                 2.确定DAG图结构；

                                 3.学习网络中每个节点CPD中的参数（即，监督学习中的参数估计）

网络参数估计：假设D为所有训练数据集，A为CPD参数

a.最大似然估计 （https://www.cnblogs.com/sylvanas2012/p/5058065.html）

由贝叶斯公式可得似然度为式中的P(D|A)，最大似然估计就是求如下目标中A的值：

                                                                            

最大似然估计完全凭数据说话，没有办法加入任何人类的已有经验。

b.最大后验估计：把优化目标由似然度函数变为了后验函数，通过人为输入先验概率P(A)得到优化目标。

优化目标：（由于无论A取值如何都不影响P(D)的值，因此后两公式等价）

 

取对数得到：

两种参数估计都可以用数学推导或梯度下降的方法求解。