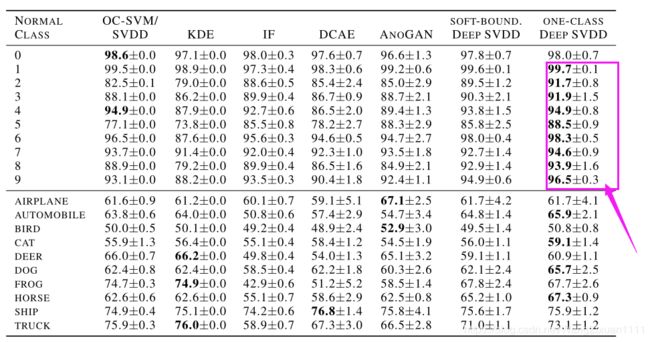
(十八)Deep One-Class Classification
论文信息
- 2018
- ICML
- 无监督的异常检测问题
- 数据集(3个):MNIST+CIFAR-10图像基准数据集+GTSRB停止标志数据集
论文原文下载链接:
Deep One-Class Classification
论文对应代码:
https://github.com/lukasruff/Deep-SVDD
论文解析参考链接
1、文章相关概念理解整理归纳:关于OCSVM与SVDD的理解
2、相关理解参考:https://www.cnblogs.com/wj-1314/p/10701708.html
2、论文解析参考:https://blog.csdn.net/zpainter/article/details/88619865
一、论文动机
1、传统的异常检测方法
(1) One-Class SVM 单分类SVM (OCSVM):最优超平面,坐标原点被假定为唯一的异常样本
(2) SVDD(support vector domain description,支持向量域描述)基本思想是:既然只有一个class,那就训练出一个最小的超球面(超球面是指三维以上的空间中的球面,对应的二维空间中就是曲线,三维空间中就是球面),将这堆数据全部“包起来”,识别一个新的数据点时,如果这个数据点落在超球面内,就属于这个类,否则不是。
实现思路:原始数据–高维表示–Min超球体积–求得c和R。
(3) Kernel Density Estimation 核密度估计(KDE)
2、缺点
(1) 浅层特征工程。由于糟糕的计算可扩展性和维度限制,导致在高维数据场景中经常失败。为了有效,这种浅层方法通常需要大量的特征工程。
(2) 由于和矩阵的构造和操作导致a poor computational scaling,除非使用近似技术,否则规模至少为样本数的平方。
(3) 核方法需要存储支持向量,需要大量内存。
结合以上的不足及传统方法的特点,本文提出了一种新的深度异常检测的方法,灵感来源于基于核的单分类问题(OCSVM)以及最小体积估计(SVDD)。
二、论文方法
1、方法简介
本文引入了一种基于核的单类分类和最小容量估计的深度异常检测(AD)的新方法——Deep Support
Vector Data Description (Deep SVDD)
(1)核心思想:训练一个神经网络,同时最小化包含数据网络表示的超球面的体积(见图1),提取数据分布变化的共同因素;
(2)神经网络转换尝试将大部分数据网络表示映射到以中心c和半径R为最小体积的超球中(在后面的数学推导中,我们的目的就是求c和R)
(3)正常例子的映射在超球面内,而异常的映射在超球面外。
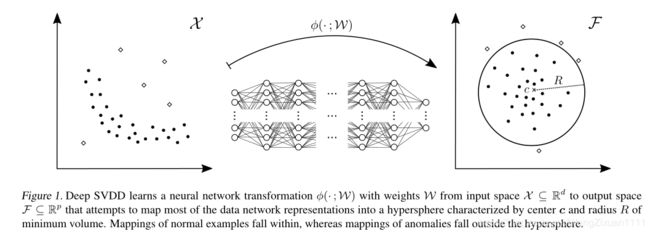
X是输入空间,Z是输出空间,![]() 表示的是具有L个隐含层的神经网络,对应权重集W={W1,W2,……Wl},深度SVDD的目标是训练神经网络的训练,让它学习一种转换,使以预定点c为中心的输出空间Z中的封闭数据超球的体积最小化
表示的是具有L个隐含层的神经网络,对应权重集W={W1,W2,……Wl},深度SVDD的目标是训练神经网络的训练,让它学习一种转换,使以预定点c为中心的输出空间Z中的封闭数据超球的体积最小化
2、方法的具体实现(两种)
(1)Soft-bound Deep SVDD——联合学习参数W和最小化在输出空间包含数据的超球的体积
目标函数如下:
第一项最小化超球体积。
第二项是对那些位于超球外的惩罚项,超参v控制超球体积和超过边界的一个权衡。如果v大,就允许一定的超出,如果v很小,超出一点就施以很大的惩罚。
第三项是网络参数W上的权重衰减正则化。
(2)One-Class Deep SVDD
目标函数如下:
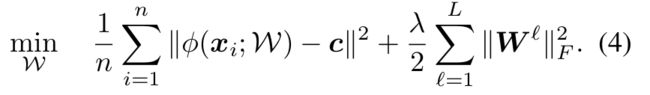
第一项,使用二次损失来惩罚每个网络表示到超球中心的距离。惩罚映射样本到超球面中心c的平均平方距离,迫使网络提取数据集中最稳定的常见变异因子。因此,正常数据点往往在超球面中心附近绘制,而异常数据点则在更远的地方绘制
第二项,网络权重衰减正则项,λ是超参。
One-Class Deep SVDD也可以视为找到最小体积的超球。 但与Soft-bound Deep SVDD不同,deep SVDD通过直接惩罚半径和落在球体外的数据表示而收缩球体,One-Class Deep SVDD通过最小化所有数据表示到中心的平均距离来收缩球体。 同样,为了将数据(平均)尽可能映射到接近中心c,神经网络必须提取变异的共同因子。 对所有数据点上的平均距离进行惩罚而不是允许某些点落在超球外,这与大多数训练数据来自一个类的假设是一致的。
异常分数的计算:测试点到超球中心点c的距离
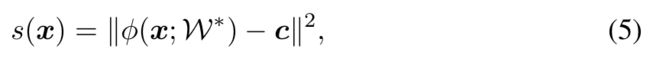
异常分数可以用上式来计算,异常样本结果为正,正常样本结果为负。