实现图的遍历算法
一、图的深度优先概述
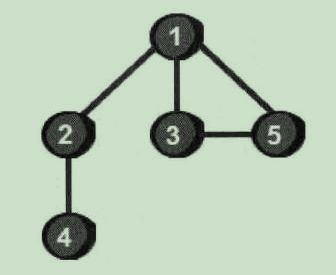
图,就是由一些小圆点(称为顶点)和连接这些小圆点的直线(称为边)组成的。例如:
上图是由五个顶点(编号为1、2、3、4、5)和五条边(1-2、1-3、1-5、2-4、3-5)组成。
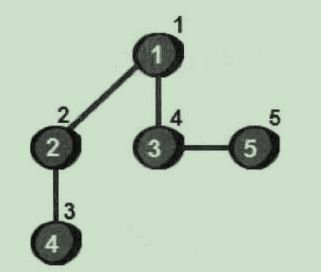
现在从1号顶点开始遍历这个图(遍历指的是把每一个顶点都访问一次)。使用深度优先搜索来遍历这个图得到以下结果:
使用深度优先搜索来遍历这个图的具体过程是:
- 首先从一个未走到过的顶点作为起始顶点,比如1号顶点作为起点。
- 沿1号顶点的边去尝试访问其它未走到过的顶点,首先发现2号顶点还没有走到过,于是来到了2号顶点。
- 再以2号顶点作为出发点继续尝试访问其它未走到过的顶点,这样又来到了4号顶点。
- 再以4号顶点作为出发点继续尝试访问其它未走到过的顶点。
- 但是,此时沿4号顶点的边,已经不能访问到其它未走到过的顶点了,所以需要返回到2号顶点。
- 返回到2号顶点后,发现沿2号顶点的边也不能再访问到其它未走到过的顶点。此时又会来到3号顶点(2->1->3),再以3号顶点作为出发点继续访问其它未走到过的顶点,于是又来到了5号顶点。
- 至此,所有顶点都走到过了,遍历结束。
深度优先遍历的主要思想是:
- 首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
- 当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
用一句话来形容 “一路走到头,不撞墙不回头”。
二、图的深度优先实现
深度优先搜索遍历是沿着图的某一条分支遍历直到末端,然后回溯,再沿着另一条进行同样的遍历,直到所有的顶点都被访问过为止。
三、图的广度优先遍历
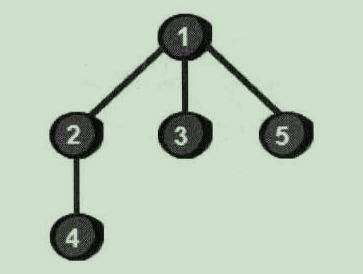
使用广度优先搜索来遍历这个图:
这五个顶点被访问的顺序如下图所示:
四、图的广度优先实现过程
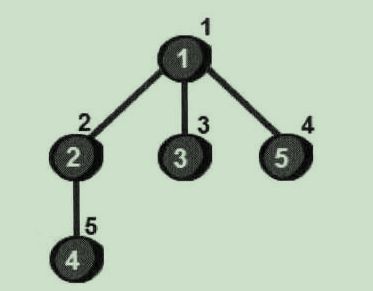
- 首先以一个未被访问过的顶点作为起始顶点,比如以1号顶点为起点。
- 将1号顶点放入到队列中,然后将与1号顶点相邻的未访问过的顶点,即2号、3号和5号顶点依次放入到队列中。
- 接下来再将2号顶点相邻的未访问过的4号顶点放入到队列中。
- 到此所有顶点都被访问过,遍历结束。
五、广度优先遍历的主要思想:
- 首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点;
- 然后对每个相邻的顶点,再访问它们相邻的未被访问过的顶点;
- 直到所有顶点都被访问过,遍历结束。
/**
* 实验题目:
* 实现图的遍历算法
* 实验目的:
* 领会图的两种遍历算法
* 实验内容:
* 编写程序,实现图的两种遍历运算,并在此基础上设计一个程序,完成如下功能:
* 1、输出如图8-1所示的有向图G从顶点0开始的深度优先遍历序列(递归算法)
* 2、输出如图8-1所示的有向图G从顶点0开始的深度优先遍历序列(非递归算法)
* 3、输出如图8-1所示的有向图G从顶点0开始的广度优先遍历序列
*/
图8-1
#include
#include
#define INF 32767 //定义∞
#define MAXV 100 //最大顶点个数
typedef char InfoType;
/*-------------------------以下定义邻接矩阵类型---------------------------*/
typedef struct
{
int no; //顶点编号
InfoType info; //顶点信息
}VertexType; //顶点类型
typedef struct
{
int edges[MAXV][MAXV]; //邻接矩阵数组(用一个二维数组存放顶点间关系(边或弧)的数据)
int n; //顶点数
int e; //边数
VertexType vexs[MAXV]; //存放顶点信息(用一个一维数组存放图中所有顶点数据)
}MatGraph; //完整的图邻接矩阵类型
//邻接表表示法-将每个顶点的邻接点串成一个单链表
/*-----------以下定义邻接表类型--------------*/
typedef struct ArcNode
{
int adjvex; //该边的邻接点编号
struct ArcNode *nextarc; //指向下一条边的指针
int weight; //该边的相关信息,如权值(用整型表示)
}ArcNode; //边结点类型
typedef struct VNode
{
InfoType info; //顶点其他信息
int cnt; //存放顶点入度,仅用于拓扑排序
ArcNode *firstarc; //指向第一条边
}VNode; //邻接表结点类型
typedef struct
{
VNode adjlist[MAXV]; //邻接表头结点数组
int n; //图中顶点数
int e; //图中边数
}AdjGraph; //完整的图邻接表类型
/*-------------------------邻接矩阵的基本运算算法---------------------------*/
/*------------由边数组A、顶点数n和边数e创建图的邻接矩阵g--------------------*/
void CreateMat(MatGraph &g, int A[MAXV][MAXV], int n, int e)
{
int i, j;
g.n = n;
g.e = e;
for(i = 0; i < g.n; i++)
for(j = 0; j < g.n; j++)
g.edges[i][j] = A[i][j];
}
/*------------输出邻接矩阵g--------------------*/
void DispMat(MatGraph g)
{
int i, j;
for(i = 0; i < g.n; i++)
{
for(j = 0; j < g.n; j++)
{
if(g.edges[i][j] != INF)
printf("%4d", g.edges[i][j]);
else
printf("%4s", "∞");
}
printf("\n");
}
}
/*-------------------------邻接表的基本运算算法---------------------------*/
/*-------------------由边数组A、顶点数n和边数e创建图的邻接表G--------------------*/
void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
int i, j;
ArcNode *p;
G = (AdjGraph *)malloc(sizeof(AdjGraph));
for(i = 0; i < n; i++) //给邻接表中所有头结点的指针域置初值NULL
{
G->adjlist[i].firstarc = NULL;
}
for(i = 0; i < n; i++) //检查邻接矩阵中的每个元素
{
for(j = n - 1; j >= 0; j--)
{
if(A[i][j] != 0 && A[i][j] != INF) //存在一条边
{
p = (ArcNode *)malloc(sizeof(ArcNode)); //创建一个结点p
p->adjvex = j; //邻接点编号
p->weight = A[i][j]; //边的权重
p->nextarc = G->adjlist[i].firstarc; //采用头插法插入结点p
G->adjlist[i].firstarc = p;
}
}
}
G->n = n;
G->e = e;
}
/*-------------------输出邻接表G--------------------*/
void DispAdj(AdjGraph *G)
{
ArcNode *p;
for(int i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
printf("顶点%d: ", i);
while(p != NULL)
{
printf("%3d[%d]->", p->adjvex, p->weight); //邻接点编号[权重]
p = p->nextarc;
}
printf("∧\n");
}
}
/*-------------------销毁图的邻接表G--------------------*/
void DestroyAdj(AdjGraph *&G)
{
ArcNode *pre, *p;
for(int i = 0; i < G->n; i++)
{
pre = G->adjlist[i].firstarc; //pre指向第i个单链表的首结点
if(pre != NULL)
{
p = pre->nextarc;
while(p != NULL) //释放第i个单链表的所有边结点
{
free(pre);
pre = p;
p = p->nextarc;
}
free(pre);
}
}
free(G); //释放头结点数组
}
int visited[MAXV]; //全局数组
/*-----------------以递归的方法从顶点v深度优先遍历图G-------------------*/
void DFS(AdjGraph *G, int v) //递归深度优先遍历算法
{
ArcNode *p;
printf("%3d", v);
visited[v] = 1; //访问顶点v,并置已访问标记
p = G->adjlist[v].firstarc; //p指向顶点v的第一条弧的弧头结点
while(p != NULL)
{
if(visited[p->adjvex] == 0) //若p->adjvex(图的邻接点编号)顶点未访问,递归访问它
DFS(G, p->adjvex);
p = p->nextarc; //p指向顶点v的下一条弧的弧头结点
}
}
/*-----------------以非递归的方法从顶点v深度优先遍历图G-------------------*/
void DFS1(AdjGraph *G, int v) //非递归深度优先遍历算法
{
ArcNode *p;
int st[MAXV]; //栈
int top = -1; //栈顶指针
int i;
int x;
int adjvex; //图中邻接点编号(顶点)
for(i = 0; i < G->n; i++) //顶点访问标志均置为0
{
visited[i] = 0;
}
printf("%3d", v); //访问顶点v
visited[v] = 1; //置顶点v已访问
top++;
st[top] = v; //将顶点v进栈
while(top > -1) //栈非空循环
{
x = st[top]; //取栈顶顶点x作为当前顶点
p = G->adjlist[x].firstarc; //找顶点x的第一个相邻点
while(p != NULL)
{
adjvex = p->adjvex; //x的相邻点为adjvex
if(visited[adjvex] == 0) //若顶点adjvex没有访问
{
printf("%3d", adjvex); //访问顶点adjvex
visited[adjvex] = 1; //置顶点adjvex已访问
top++; //将顶点adjvex进栈
st[top] = adjvex;
break; //退出循环,即再处理栈顶的顶点(体现后进先出)
}
p = p->nextarc; //找顶点x的下一个相邻点
}
if(p == NULL) //若顶点x再没有相邻点,将其退栈
top--;
}
printf("\n");
}
/*-----------------从顶点v广度优先遍历图G-------------------*/
void BFS(AdjGraph *G, int v) //广度优先遍历算法
{
ArcNode *p;
int graph_queue[MAXV], queue_front = 0, queue_rear = 0; //定义环形队列并初始化
int visited[MAXV]; //定义存放顶点的访问标志的数组
int i;
int adjvex;
for(i = 0; i < G->n; i++)
{
visited[i] = 0; //访问标志数组初始化
}
printf("%3d ", v); //输出被访问顶点的编号
visited[v] = 1; //置已访问标记
queue_rear = (queue_rear + 1) % MAXV;
graph_queue[queue_rear] = v; //v进队
while(queue_front != queue_rear) //若队列不空时循环
{
queue_front = (queue_front + 1) % MAXV;
adjvex = graph_queue[queue_front]; //出队列并赋给adjvex
p = G->adjlist[adjvex].firstarc; //找顶点adjvex的第一个相邻点
while(p != NULL)
{
if(visited[p->adjvex] == 0) //若相邻点未被访问
{
printf("%3d ", p->adjvex); //访问相邻点
visited[p->adjvex] = 1; //置该顶点已被访问的标志
queue_rear = (queue_rear + 1) % MAXV; //该顶点进队
graph_queue[queue_rear] = p->adjvex;
}
p = p->nextarc; //找下一个相邻点
}
}
printf("\n");
}
int main(void)
{
AdjGraph *G;
int n = 6; //图中的顶点数
int e = 10; //图中的边数
int A[MAXV][MAXV] = {
{0, 5, INF, 7, INF, INF}, {INF, 0, 4, INF, INF, INF},
{8, INF, 0, INF, INF, 9}, {INF, INF, 5, 0, INF, 6},
{INF, INF, INF, 5, 0, INF}, {3, INF, INF, INF, 1, 0}
};
CreateAdj(G, A, n, e);
printf("图的邻接表:\n");
DispAdj(G);
printf("从顶点0开始的DFS(递归算法):\n");
DFS(G, 0);
printf("\n");
printf("从顶点0开始的DFS(非递归算法):\n");
DFS1(G, 0);
printf("从顶点0开始的BFS:\n");
BFS(G, 0);
printf("销毁图的邻接表\n");
DestroyAdj(G);
return 0;
}
测试结果:
图的邻接表:
顶点0: 1[5]-> 3[7]->∧
顶点1: 2[4]->∧
顶点2: 0[8]-> 5[9]->∧
顶点3: 2[5]-> 5[6]->∧
顶点4: 3[5]->∧
顶点5: 0[3]-> 4[1]->∧
从顶点0开始的DFS(递归算法):
0 1 2 5 4 3
从顶点0开始的DFS(非递归算法):
0 1 2 5 4 3
从顶点0开始的BFS:
0 1 3 2 5 4
销毁图的邻接表