字符串模式匹配KMP算法

嗯，第一次学习KMP算法，做些笔记，肯定会有许多不足之处，以后还会不断更新修改。。。
KMP字符串模式匹配算法通俗点说就是一种在一个字符串中定位另一个串的高效算法。朴素的模式匹配算法的时间复杂度为O(m*n);而KMP模式匹配算法的时间复杂度则为O(m+n)。
朴素的模式匹配算法
很直观的可以写出下面的代码，来找出模式串在一个长字符串中出现的位置。

/*
      朴素的模式匹配算法
      功能:字符串的模式匹配
      参数：
          s:目标串
          p:模式串
      返回值：
          匹配成功，返回模式串在目标串的其实位置
          匹配不成功，返回-1
*/
int match(const char *s,const char *p,int pos)
{
    int i=pos;
    int j=0;
    while(s[i]!='\0'&&p[j]!='\0')
    {
        if(s[i]==p[j])
        {   
            i++;
            j++;
        }   
        else
        {
            i=i-j+1;
            j=0;
        }
    }
    if(p[j]=='\0')
        return i-j;
    else
        return -1;
}

上面的代码，s就是目标串，p是模式串，pos指定从s的什么位置开始匹配p。其实现思想也很简单：

当s[i] == p[j]时，目标串和模式串的指针都向后移动一位，进行匹配。而当s[i] != p[j]时，即匹配不成功时，将目标串和模式串的指针同时回溯，j = 0 而目标串的指针i则回溯到这一轮开始时的后一个位置。

朴素的模式匹配的算法复杂度是O( (n-m+1) * m) ，其中 n为目标串的长度，m为模式串长度。

从其实现思想上可以很容易的看出，造成该算法低效的地方在于：匹配不成功时主串和模式串的指针回溯上。

有没有一种算法，当模式串和主串的匹配不成功时，不用进行指针的回溯，直接进行下一轮的匹配？
ＫＭＰ算法理解：
在朴素的字符串模式匹配算法上，当遇到主串和模式串的字符不能匹配成功时，不论已经匹配了多少字符都要进行指针回溯，再开始下一轮的匹配。这样处理效率是十分低下的。而ＫＭＰ算法，则是在朴素的模式匹配算法的基础上，实现了匹配不成功时，不对主串指针进行回溯，使模式匹配的时间复杂度降低为：O(n + m)。
我们可以想像着将模式串、主串都看成是条直线，然后进行推导，你可能会恍然大悟。

KMP算法的核心思想是，在s[i] 和 p[j]不匹配时，不对主串进行指针回溯，而是在模式串p中寻找一个位置下标k，用s[i] 和 p[k]进行下一轮的匹配。

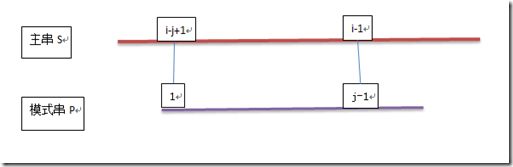
在这里，将主串 S 和模式串 P 都看成是一条直线，故而在S[i] 和 P[j] 匹配不成功时，有如下情形：

图1 s[i] 和 p[j] 匹配不成功

即是：p[1…j-1] == s[i-j+1,…,i-1].

p[j] 和 s[i] 不匹配，现在要在模式串p[1,…,j-1]确定一个位置k（1<= k < j-1)，用p[k]和s[i]进行下一轮匹配，那么k必须要满足以下条件：

p[1,..,k-1] == s[i-k+1, … , i-1] .

将模式串和主串都看着一条直线，那么就有下图：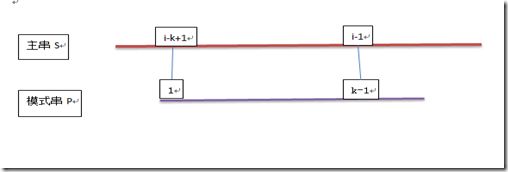
图2 使用p[k]和s[i]进行下一轮匹配

由于 1<= k < j-1，那么将两图合并起来会有什么效果呢？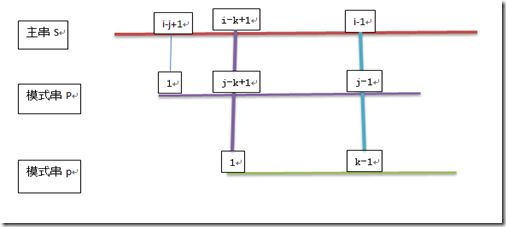

从上图可以看出，当s[i]和p[j]匹配不成功时，假如能用p[k]和s[i]进行下一轮匹配，则有：

s[i-k+1], … , i-1] == p[j-k+1,…,j-1] == p[1,…,k-1] 。

就是说，当s[i] 和 p[j] 匹配不成功时，对主串不进行指针回溯，而是用p[k]和s[i]进行匹配时，k必须满足以下条件：
p[1,…,k-1] == p[j-k+1, … , j-1]。

KMP算法的实现

KMP算法是对朴素的模式匹配算法的改进，在s[i]和p[j]匹配不成功时，不是对主串进行指针的回溯，而是在p[1,…,j-1]中，寻找一个p[k],用s[i]和p[k]进行下一轮的匹配。其实现的最大问题就是如何根据p[1,…,j-1]来求出p[k]。

在KMP算法的实现中，使用一个辅助数组next[],使用该数组保存p[j]匹配不成功时，要进行下一轮匹配的k的值。即当s[i] 和 p[j]匹配不成功时，用p[ next[j] ]来和s[i]进行下一轮匹配，即k = next[j] .

对数组next[] 的求解，可以goolge到不少的方法，这里使用最简单的递推的方法：

首先假定next[0] = –1,那么当next[j] = k时，就有：p[0,…,k-1] = p[j-k+1,…,j-1]。

这时，若有p[k] = p[j] ，则p[0,….,k] = p[j-k+1,..,j-1,j]，从而就有next[j+1] = next[j] + 1 = k +1 .

若p[k] != p[j] ,可以看着模式串对自身进行匹配的问题，即当匹配失败的时候，k值如何确定，k = next [k] .

求数组next[ ]的实现如下：

/*
    KMP进行模式匹配的辅助函数
    用于得到next数组
*/
void get_next(const char *p,int *next)
{
    int j;
    int k;
    next[0]=-1;
    j=0;
    k=-1;
    while(j1)
    {
        if(k==-1 || p[k]==p[j])
        {
            j++;
            k++;
            next[j]=k;
        }
        else
        {
            k=next[k];
        }
    }
}

知道了当模式串和主串匹配不成功时，下一个和主串匹配的字符在模式串中的位置，在朴素的模式匹配的基础上很容易的写出KMP算法的代码如下：

/*
    运用KMP算法的字符串模式匹配
    在主串和模式串匹配不成功时，不对主串指针进行回溯，
    用next[j]来指定下一次和主串进行匹配的模式串的位置
*/
int match_kmp(const char * s ,const char * p,int pos)
{
    int next[11] ;
    int i = pos ;
    int j = 0 ;
    get_next(p,next) ;
    while(s[i] != '\0' && p[j] != '\0')
    {
        if(s[i] == p[j])
        {
            i++;
            j++;
        }
        else
        {
            if(next[j] == -1)
            {
                i++;
                j=0;
            }
            else
            {
                j=next[j] ;
            }
        }
    }
    if(p[j]=='\0')
        return i-j ;
    else
        return -1 ;
}