2D-2D:E2RT_Triangulation
2D-2D:E2RT_Triangulation
- 引言
- 1.2D-2D对极约束
- 2.八点法求解E
- 3.三角测量求深度
引言
ch7.task5_3.当相机为单目时,只知道2D的像素坐标,因而问题是根据两组2D点估计运动。该问题用对极几何来解决。
1.2D-2D对极约束
实际求解步骤:
- (1)根据已经匹配的像素点 x 1 , x 2 x_1,x_2 x1,x2由公式 x 2 T t ∧ R x 1 = 0 x_2^Tt^{\wedge}Rx_1=0 x2Tt∧Rx1=0使用八点法求解 ( t ∧ R ) 3 ∗ 3 (t^{\wedge}R)_{3*3} (t∧R)3∗3即求解本质矩阵 E E E.
- (2)根据本质矩阵 E E E使用奇异值分解(SVD), E = U Σ V T E=U\Sigma V^T E=UΣVT求出 R , t R,t R,t.


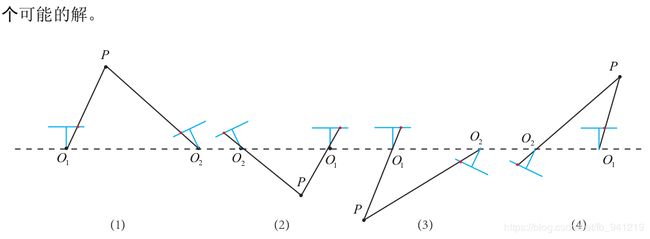
由图可以看出,只有图(1)是真正的解。只需要把任意一点代入四种解中,检测该点在两个相机下的深度,就可以确定哪个解是正确的。对于单目初始化不能只有纯旋转,必须要有一定程度的平移。具体参考教材 P 155 P_{155} P155.
E2Rt code:
#include
#include
#include
using namespace Eigen;
#include
using namespace Sophus;
#include
using namespace std;
int main(int argc, char **argv) {
// 给定Essential矩阵
Matrix3d E;//3*3
E << -0.0203618550523477, -0.4007110038118445, -0.03324074249824097,
0.3939270778216369, -0.03506401846698079, 0.5857110303721015,
-0.006788487241438284, -0.5815434272915686, -0.01438258684486258;
// 待计算的R,t
Matrix3d R;
Vector3d t;
// SVD and fix singular values(奇异值)
// START YOUR CODE HERE
//E = U*Sigma*VT ==> Sigma = U.inv()*E*VT.inv()
JacobiSVD svd(E, ComputeThinU | ComputeThinV);
Matrix3d U = svd.matrixU(); // Obtain matrix U
Matrix3d V = svd.matrixV(); // Obtain matrix V
Matrix3d Sigma = U.inverse() * E * V.transpose().inverse(); // Obtain matrix Sigma
cout<<"U:\n"< tao = {Sigma(0,0), Sigma(1,1), Sigma(2,2)};//是小写的sigma不是tao
sort(tao.begin(),tao.end());//从大到小排序 Sigma = diag(sigma1,sigma2,sigma3);
double tao_mean = (tao[1]+tao[2])*0.5;
Matrix3d SigmaFix = Matrix3d::Zero(); // SigmaFix: 處理后的Sigma矩陣
SigmaFix(0,0) = tao_mean;
SigmaFix(1,1) = tao_mean;
cout<<"Sigma after fix: \n"<
当点对多余8对且可能存在误匹配的情况时,会更倾向于使用随机采样一致性(Random Sample Concensus,RANSAC)求解,而不是最小二乘。RANSAC是一种通用的做法,适用于很多带错误数据的情况,可以处理带有错误匹配的数据。
RANSAC算法参考:
- 参考链接1
- 参考链接2
- 参考链接3
- 参考链接4
像点总是在对极线,因此可以选择像点到对极线的距离作为判断该点是内点还是外点的依据,设点到对极的距离的阈值为d。则使用RANSAC的方法估算基础矩阵的步骤:
- 从匹配的点对中选择8个点,使用8点法估算出基础矩阵 F i F_i Fi
- 计算其余的点对到其对应对极线的距离 d n d_n dn,如果 d n ≤ d d_n≤d dn≤d则该点为内点,否则为外点。记下符合该条件的内点的个数为 m i m_i mi
- 迭代k次,或者某次得到内点的数目 m i m_i mi占有的比例大于等于95%,则停止。选择 m i m_i mi最大的基础矩阵作为最终的结果。
RANSAC能够不依赖于任何额外信息的情况下,将数据划分为内点和外点。但也有其相应的缺点,RANSAC并不能保证得到正确的结果,需要提高迭代的次数;另一个是,内点外点的判断需要设置阈值。
3.三角测量求深度
对于单目SLAM的地图点深度估计,依靠两帧匹配的图像实现(但是具有尺度不确定性)。
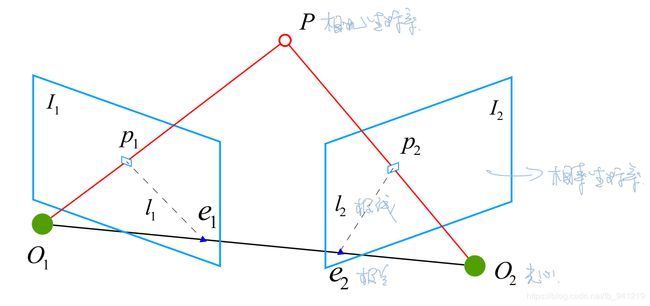
- 归一化平面: s 1 x 1 = s 2 R x 2 + t s_1x_1=s_2Rx_2+t s1x1=s2Rx2+t,其中的 R , t R,t R,t已经知道。
- 左乘 x 1 ∧ x_1^{\wedge} x1∧得: s 1 x 1 ∧ x 1 = 0 = s 2 x 1 ∧ R x 2 + x 1 ∧ t s_1x_1^{\wedge}x_1=0=s_2x_1^{\wedge}Rx_2+x_1^{\wedge}t s1x1∧x1=0=s2x1∧Rx2+x1∧t,根据右侧求解出 s 2 s_2 s2,然后一次求出 s 1 s_1 s1就得到了深度。
- 由于噪声的存在,估得的 R, t,不一定精确使式 s 1 x 1 = s 2 R x 2 + t s_1x_1=s_2Rx_2+t s1x1=s2Rx2+t为0,所以常用的最小二乘解而不是零解。
CODE:从2D图像进行ORB特征提取–>特征匹配–>极线约束八点法求E(F、H)–>R,t–>三角测量求深度
/*
*三角测量法 求解 两组单目相机 图像点深度
* s1 * x1 = s2 * R * x2 + t
* x1 x2 为两帧图像上 两点对 在归一化坐标平面上的坐标
* s1 和 s2为两个特征点的深度 ,由于误差存在, s1 * x1 = s2 * R * x2 + t不精确相等
* 常见的是求解最小二乘解,而不是零解
* s1 * x1叉乘x1 = s2 * x1叉乘* R * x2 + x1叉乘 t=0 可以求得x2
*
*/
#include
#include
#include
#include
#include
// #include "extra.h" // used in opencv2
using namespace std;//标准库 命名空间
using namespace cv; //opencv库命名空间
// ./pose_estimation_2d2d 1.png 2.png
/****************************************************
* 本程序演示了如何使用2D-2D的特征匹配估计相机运动 基于三角测量
* **************************************************/
//特征匹配 计算匹配点对
void find_feature_matches (
const Mat& img_1, const Mat& img_2,
std::vector& keypoints_1,
std::vector& keypoints_2,
std::vector< DMatch >& matches );
//位置估计 计算旋转和平移 第一张图 到第二章图的坐标变换矩阵和平移矩阵
void pose_estimation_2d2d (
const std::vector& keypoints_1,
const std::vector& keypoints_2,
const std::vector< DMatch >& matches,
Mat& R, Mat& t );
// 三角测量
void triangulation (
const vector& keypoint_1,
const vector& keypoint_2,
const std::vector< DMatch >& matches,
const Mat& R, const Mat& t,
vector& points
);
// 像素坐标转相机归一化坐标
Point2f pixel2cam( const Point2d& p, const Mat& K );
int main ( int argc, char** argv )
{
if ( argc != 3 )//命令行参数 1.png 2.png
{
cout<<"用法: ./triangulation img1 img2"< keypoints_1, keypoints_2;//关键点初始化
vector matches;//特征点匹配对初始化
find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
cout<<"一共找到了"< points;
triangulation( keypoints_1, keypoints_2, matches, R, t, points );
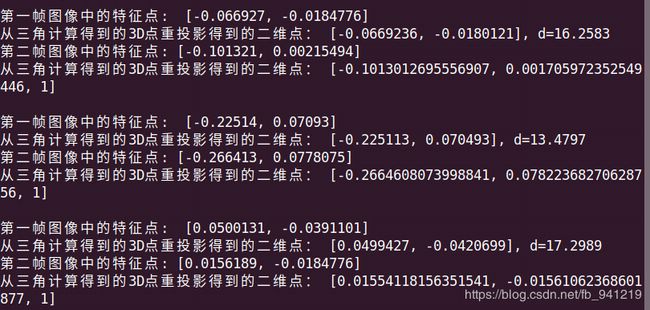
//-- 验证三角化点与特征点的重投影关系
Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );// 相机内参,TUM Freiburg2
for ( int i=0; i& keypoints_1,
std::vector& keypoints_2,
std::vector< DMatch >& matches )
{
//--------------------第0步:初始化------------------------------------------------------
Mat descriptors_1, descriptors_2;//描述子
// OpenCV3 特征点检测器 描述子生成器 用法
Ptr detector = ORB::create();
Ptr descriptor = ORB::create();
// OpenCV2 特征点检测器 描述子生成器 用法
// Ptr detector = FeatureDetector::create ( "ORB" );
// Ptr descriptor = DescriptorExtractor::create ( "ORB" );
Ptr matcher = DescriptorMatcher::create("BruteForce-Hamming");;//汉明点对匹配
//------------------第一步:检测 Oriented FAST 角点位置-----------------------------
detector->detect ( img_1,keypoints_1 );
detector->detect ( img_2,keypoints_2 );
//------------------第二步:根据角点位置计算 BRIEF 描述子-------------------------
descriptor->compute ( img_1, keypoints_1, descriptors_1 );
descriptor->compute ( img_2, keypoints_2, descriptors_2 );
//------------------第三步:对两幅图像中的BRIEF描述子进行匹配,使用 Hamming 距离
vector match;
// BFMatcher matcher ( NORM_HAMMING );
matcher->match ( descriptors_1, descriptors_2, match );
//-----------------第四步:匹配点对筛选--------------------------------------------------
double min_dist=10000, max_dist=0;
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for ( int i = 0; i < descriptors_1.rows; i++ )
{
double dist = match[i].distance;
if ( dist < min_dist ) min_dist = dist; //最短距离 最相似
if ( dist > max_dist ) max_dist = dist; //最长距离 最不相似
}
printf ( "-- Max dist : %f \n", max_dist );
printf ( "-- Min dist : %f \n", min_dist );
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
for ( int i = 0; i < descriptors_1.rows; i++ )
{
if ( match[i].distance <= max ( 2*min_dist, 30.0 ) )
{
matches.push_back ( match[i] );
}
}
}
//特征匹配 计算匹配点对 函数 第一张图 到第二章图的坐标变换矩阵和平移矩阵
//对极几何
void pose_estimation_2d2d (
const std::vector& keypoints_1,
const std::vector& keypoints_2,
const std::vector< DMatch >& matches,
Mat& R, Mat& t )
{
// 相机内参,TUM Freiburg2
Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
//-- 把匹配点转换为vector的形式
vector points1;
vector points2;
for ( int i = 0; i < ( int ) matches.size(); i++ )
{
points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
}
//-- 计算基础矩阵 F
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
cout<<"fundamental_matrix is "<& keypoint_1,
const vector< KeyPoint >& keypoint_2,
const std::vector< DMatch >& matches,
const Mat& R, const Mat& t, //特征匹配 计算匹配点对 函数 第一张图 到第二章图的坐标变换矩阵和平移矩阵
//对极几何
vector< Point3d >& points )
{
// 变换矩阵 在第一幅图像下 的变换矩阵 Pc1 = Pw = T1 * Pw
Mat T1 = (Mat_ (3,4) <<
1,0,0,0,
0,1,0,0,
0,0,1,0);
// Pc2 = T2 * Pw = [ R t] * Pw
Mat T2 = (Mat_ (3,4) <<
R.at(0,0), R.at(0,1), R.at(0,2), t.at(0,0),
R.at(1,0), R.at(1,1), R.at(1,2), t.at(1,0),
R.at(2,0), R.at(2,1), R.at(2,2), t.at(2,0)
);
// 相机内参,TUM Freiburg2
// [fx 0 cx
// 0 fy cy
// 0 0 1]
Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
vector pts_1, pts_2;//相机坐标下点坐标
for ( DMatch m:matches )
{
// 将像素坐标转换至相机坐标
pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
}
Mat pts_4d;//三角测量得到的 三维空间点 其次坐标
cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
// 转换成非齐次坐标
for ( int i=0; i(3,0); // 归一化
Point3d p (
x.at(0,0),
x.at(1,0),
x.at(2,0)
);
points.push_back( p );
}
}
// 像素坐标转相机归一化坐标
Point2f pixel2cam ( const Point2d& p, const Mat& K )
{
return Point2f
(
( p.x - K.at(0,2) ) / K.at(0,0),
( p.y - K.at(1,2) ) / K.at(1,1)
);
}