电路分析笔记-电阻电路的等效变换

电路的等效变换

两端网络（网络）

任何一个复杂的电路, 向外引出两个端钮，且从一个端子流入的电流等于从另一端子流出的电流，则称这一电路为二端网络 (或一端口网络)。

两端电路等效的概念

两个两端电路，端口具有相同的电压、电流关系,则称它们是等效的电路。

电路等效变换的条件：两电路具有相同的VCR。

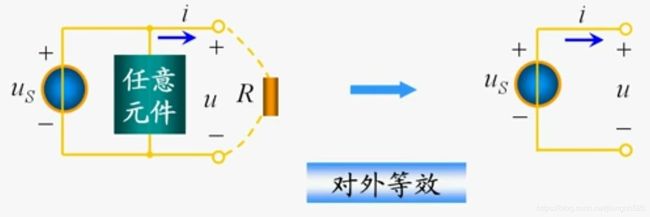
电路等效变换的对象：未变化的外电路A中的电压、电流和功率；（即对外等效，对内不等效）

电路等效变换的目的：化简电路，方便计算。

串联电路的总电阻等于各分电阻之和

等效电导等于并联的各电导之和。

串联电阻分压：电压与电阻成正比，因此串联电阻电路可作分压电路。

并联电阻分流：电流分配与电导成正比

串联电阻功率

①电阻串联时，各电阻消耗的功率与电阻大小成正比；

②等效电阻消耗的功率等于各串联电阻消耗功率的总和。

并联电阻功率

①电阻并联时，各电阻消耗的功率与电阻大小成反比；

②等效电阻消耗的功率等于各并联电阻消耗功率的总和

解串、并联电路一般步骤

①求出等效电阻或等效电导

②应用欧姆定律求出总电压或总电流

③应用欧姆定律或分压、分流公式求各电阻上的电流和电压

电阻的Y形连接和△形连接的等效变换

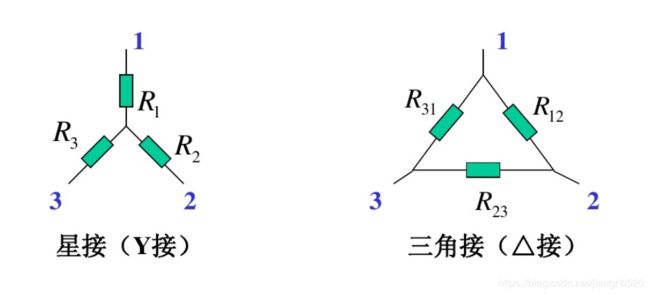
Y形等效△形公式：

$$R_{12}=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_3}$$

$$R_{23}=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_1}$$

$$R_{31}=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_2}$$

△形等效Y形公式：

$$R_1=\frac{R_{12}{R}_{31}}{R_{12}+R_{23}+R_{31}}$$

$$R_2=\frac{R_{12}{R}_{23}}{R_{12}+R_{23}+R_{31}}$$

$$R_3=\frac{R_{23}{R}_{31}}{R_{12}+R_{23}+R_{31}}$$

惠斯通电桥

一种由4个电阻组成用来测量其中一个电阻阻值(其余3个电阻阻值已知)的装置。4个电阻组成一个方形。

一电流表连接两个相对的接头，一电流表连接其余两个相对的接头。当电流表显示无电流通过，则此电桥处于平衡状态，即R1·R2=R3·R4。

电压源、电流源的串联和并联

电压源与支路的串、并联等效

相同电压源才能并联,电源中的电流不确定。

电流源与支路的串、并联等效

相同的理想电流源才能串联, 每个电流源的端电压不能确定。

实际电源的两种模型及其等效变换

实际电压源也不允许短路。因其内阻小，若短路，电流很大，可能烧毁电源。

实际电流源也不允许开路。因其内阻大，若开路，电压很高，可能烧毁电源。

电压源和电流源的等效变换

实际电压源、实际电流源两种模型可以进行等效变换，所谓的等效是指端口的电压、电流在转换过程中保持不变。

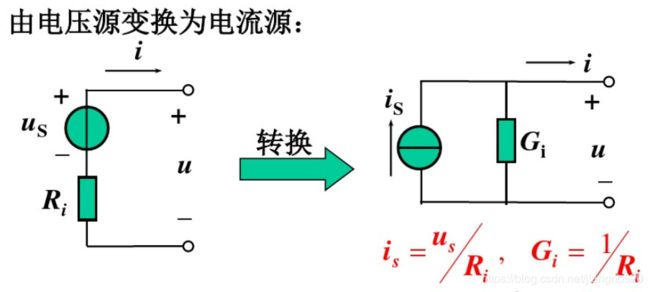
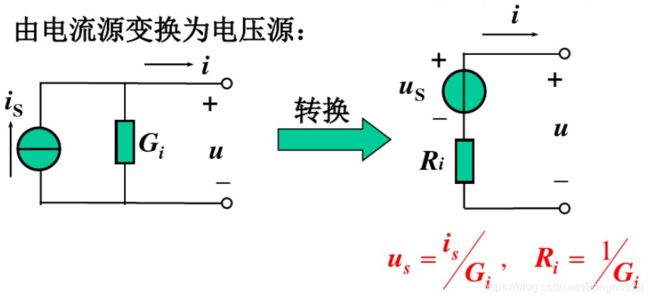
输入电阻

定义为输入电压有效值Ui和输入电流有效值Ii之比，即Ri，

计算方法

①如果一端口内部仅含电阻，则应用电阻的串、并联和D—Y变换等方法求它的等效电阻

②对含有受控源和电阻的两端电路，用电压、电流法求输入电阻，即在端口加电压源，求得电流，或在端口加电流源，求得电压，得其比值。