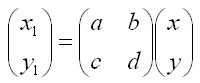《高斯数学日记》——数论
译文献给所有热爱数学的人,同时纪念一代数学大师高斯。
高斯对于正十七边形可构建性的发现源于对已知的一个重要的代数性质问题的领悟。他将17个顶点想成方程Z17-1=0的17个根,其中一个根是简单的Z=1,其余16个根满足方程Z16+Z15+…+Z+1=0。高斯认为既然17是一个素数并且16=24,那么对于其余16个根的计算可以简化为求4个二次方程的连续解问题(高斯这一重要的发现详尽地记录在《Disquisitiones》的§354)。我们是可以通过几何上的尺规作图来求解二次方程的,因此正十七边形是可以通过几何方式构建出来的,与此同时高斯也通过确切给出的4个二次方程来说明构建的方式。高斯也同样针对几何作图中的各点给出了小数点后面长达10位的复杂坐标,这也表明了高斯要先于Argand与Wessel关注复数的几何平面。但是令人难以理解的是,高斯是如何联想到这个具有深远意义的具有Zn-1=0这种形式的方程理论。在这本日记后面的条目中我们可以找寻到一些高斯在探索分圆理论的痕迹。有了这一发现,高斯决定去学习数学而不是语言学。
日记中第二个条目所记录的是与正十七边形尺规作图同等重要的二次互反定律(这一定律曾被Dunnington所忽视)。我们规定:如果全等式x2 ≡ a(mod p)有整数解(p为素数),那么我们称整数a是mod p的一个平方剩余。二次互反定律可以表述为:如果p和q是任意不同的奇素数,那么p对于q的二次特征与q对于p的二次特征相同,除非p和q都是4n+3形式的数,在这种情况下他们拥有相反的二次特征。对于素数2和数-1进行辅助说明:2是mod p的余数当且仅当p是8k±1的形式,-1是mod p的余数当且仅当p是4k-1的形式。因为一个乘积ab是mod p的一个余数当且仅当它的因子都是mod p的余数或都不是mod p的余数,这也可以用来简单判断任何一个给定的数是否是一个素数模的余数。
Dunnington曾指出:无论二次互反定律最初是在何种情况下被发现的,找出证明它的方法才是一项艰难的工作,而高斯是第一个做这项工作的人。然而高斯的第一个证明并不是令人十分满意,紧接着高斯就想到了第二个证明(看条目16)。这个证明引用了二元二次型理论(形如Ax2+2Bxy+Cy2的表达式)。
在这一理论中,核心问题是找出什么样的整数可以写成以特定整数序列A,B,C表示的形式,以及在何种情况下两个给定的二次型可以表示相同的整数序列。高斯曾给出:二次型Ax2+2Bxy+Cy2与A1x12+2B1x1y1+C1y12完全等价,当满足下列等式:
其中a,b,c,d是整数并且满足ad-bc=1。高斯也指出:这些由具有相同无平方因子判别式B2-AC的二次型所构成的等价类群是满足某种组成法则的(用现代的术语说,它们构成了一个有限交换群)。运用组合的思想去解析二次型的做法是意义深远的;Edwards称这是高斯对这一理论的重大贡献。用现代的话说,高斯所谓的关键性发现就是发现了由平方所组成的子群。高斯继Lengendre之后,称这个子群的陪集为genera。高斯在使用genera时采用genera的全称,这种命名使用方式一直沿用到现代的群表示论中。
在《Disquisitiones Arithmeticae》(§230,231)中高斯给出了一些说明性的例子。例如:二次型10x2+6xy+17y2用判别式32-10*17 = -161 = -1*7*23。以这种二次型表示的数字一定既是mod 7的非余数,又是mod 23的非余数。以这种二次型表示的奇数也一定全等于1 mod 4。以上几点构成了由二次型10x2+6xy+17y2所定义的类群的全部特征而其中的+1与-1和二次型本身有关,它们决定了由二次型所表示的数字是否是mod通过判别式分解而来的素数的余数(这就是二次型的判别原理)。在19世纪80年代期间,Weber和Dedekind在考虑到非零复数子群{±1}的情况下将高斯上述所提的特征解释为二次型群的一种同态。
事实上,一些指定的特征是不能归因于一个A、2B和C没有公约数的二次型(D.A.§261),这一事实成为了二次互反定律的第二种证明的基础(D.A.§262)。与之相关联的是在§261的二次互反理论,这一理论由高斯独立完成,因此基于这一理论的矛盾就迫使高斯推断:如果这一法则是错的,那么满足所有特征的二次型就能被轻易的写出来。
这一理论中有多少成分明显是由高斯在1796年的6月27日提出的,这并不明确。一篇称之为《Analysis Residuorum》的《Disquisitiones Arithmeticae》的现存初步版本出现在《Gauss,Werke,Ⅱ,199-240》中,更多的由U.Merzbach收录在柏林(见[Merzbach,1981])。不幸的是与之相关的第五章节至今仍然缺失,但是我们知道在1797年到1798年间高斯至少写了4次有关第五章节的内容,因为他在给W.Bolyai的一封信中曾这样提到(引自[Merzbach,1981])。一种说法是在1796年高斯已经知道了证明的方法,但不一定是所有的证明细节。
在1801年的5月中旬高斯发现了证明二次互反定律的第五种方法,高斯发现它与我们今天所谓的“高斯和”有关:
但具体的证明方法直到1805年8月30日才被高斯想到(他在给Olbers的一封信中曾提到“灵光一现,难题就被解决了”)。证明方法是基于如果
那么
找出在每种情况下和是比较容易的,困难在于找出这种现象的原因,这个问题一直萦绕在高斯的心头直至1805年。通过对高斯和的深入研究,高斯找到了解释这一现象的原因(见Berndt and Evans [1981])。
在这本日记的最后几个条目中记录了高斯在1807年将二次互反理论扩展到了立方剩余与四次方剩余,并且意外的发现了二次互反理论的第六种证明方式。当高斯在1825年到1831年间(Werke,Ⅱ 65-92和93-148)发表关于四次方剩余的论文时,他发现采用虚数理论可以很好的证明这一理论,证明所采用的虚数我们称之为高斯整数。这时Jacobi发现了立方互反定律,在19世纪40年代Eisenstein也发现了立方互反定律,并给出了证明同时又与椭圆函数理论联系到了一起。不幸的是关于这些理论的发展情况以及先后情形挑起了Collison与Weil的争论。
高斯给下一代德国数学家所遗留下来的宝贵财富不仅仅是他所发现的关于数字的重要理论。它更是理论之间高深奇特的内在联系,以及所涉及的具有深刻性的证明。当像Dirichlet一样的高斯理论的解释者为了使高斯的理论更容易被理解,将二次型用二次整数代替表示,这些解释者接受和拥护这一转换的重要性,结果导致《Disquisitiones Arithmeticae》开始了一个延续至今的惯例:数论是数学中最深奥以及最重要的分支之一。在19世纪早期诸如Alexander Humboldt的新人文主义者们崇尚顺应自然的自主学习,这使得他们很是崇拜高斯的思想理论。或许这种崇拜在1996年的时候就转到了Andrew Wiles身上,因为在1996年Andrew Wiles最终完成了费马大定理的全部证明,而这一证明震惊了整个数学界。
参考文献:
《高斯经典文章及相关数学工作汇编》Scibird
《Gauss`s Mathematical Diary》Gauss
后记:下一篇将翻译《高斯数学日记》——椭圆函数理论