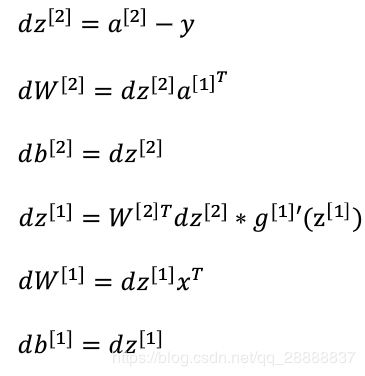反向传播（BP算法）python实现

反向传播（BP算法）python实现

1、BP算法描述

BP算法就是反向传播，要输入的数据经过一个前向传播会得到一个输出，但是由于权重的原因，所以其输出会和你想要的输出有差距，这个时候就需要进行反向传播，利用梯度下降，对所有的权重进行更新，这样的话在进行前向传播就会发现其输出和你想要的输出越来越接近了。

上面只是其简单的原理，具体实现起来其实就是利用了链式法则，逐步的用误差对所有权重求导，这样便反向得到了误差对每个权重的梯度，然后再把所有的梯度更新一下即可。

其中每一层的w的梯度可以用下面的公式计算，下面的公式是摘自吴恩达老师的笔记，这个是一个两层的网络，$d{w}^{[2]}$ 代表误差对最后一层的w的导数，$d{w}^{[1]}$ 代表第一层，其实除了最后一层，前面的可以抽象成一个公式，比如误差对第 $l$ 层（$l$ 为非最后一层）的权重的导数为$d{w}^{[l]}=d{z}^l{a}^{[l-1{]}^T}$ 其中$a^{[0]}=x$ ，这样的话我们就可以求出一个对任意层的权重的梯度了。（$z^{[l]}代表第l层未激活的输出$ $a^{[l]}代表第l层激活的输出$ ，这些基本符号的含义可以参考吴恩达笔记的定义）

并且我们从公式也可以看出来，如果计算权重的梯度，我们需要 $z、a、w$，所以我们在编制代码的时候需要注意，在进行前向传播的时候要把z和a暂存起来，这样在进行反向传播的时候就可以直接拿来用了。

Notice： 在图片中的乘分为两种，如果是ab则在python中用点乘就是a.dot(b)，而ab则在python中用ab 二者去呗是a.dot(b)就是矩阵运算，而a*b则是对应元素乘。

2、基于梯度下降的反向传播的代码实现

# 生成权重以及偏执项layers_dim代表每层的神经元个数，
#比如[2,3,1]代表一个三成的网络，输入为2层，中间为3层输出为1层
def init_parameters(layers_dim):
    
    L = len(layers_dim)
    parameters ={}
    for i in range(1,L):
        parameters["w"+str(i)] = np.random.random([layers_dim[i],layers_dim[i-1]])
        parameters["b"+str(i)] = np.zeros((layers_dim[i],1))
    return parameters

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

# sigmoid的导函数
def sigmoid_prime(z):
        return sigmoid(z) * (1-sigmoid(z))

# 前向传播，需要用到一个输入x以及所有的权重以及偏执项，都在parameters这个字典里面存储
# 最后返回会返回一个caches里面包含的 是各层的a和z，a[layers]就是最终的输出
def forward(x,parameters):
    a = []
    z = []
    caches = {}
    a.append(x)
    z.append(x)
    layers = len(parameters)//2
    # 前面都要用sigmoid
    for i in range(1,layers):
        z_temp =parameters["w"+str(i)].dot(x) + parameters["b"+str(i)]
        z.append(z_temp)
        a.append(sigmoid(z_temp))
    # 最后一层不用sigmoid
    z_temp = parameters["w"+str(layers)].dot(a[layers-1]) + parameters["b"+str(layers)]
    z.append(z_temp)
    a.append(z_temp)
    
    caches["z"] = z
    caches["a"] = a    
    return  caches,a[layers]

# 反向传播，parameters里面存储的是所有的各层的权重以及偏执，caches里面存储各层的a和z
# al是经过反向传播后最后一层的输出，y代表真实值
# 返回的grades代表着误差对所有的w以及b的导数
def backward(parameters,caches,al,y):
    layers = len(parameters)//2
    grades = {}
    m = y.shape[1]
    # 假设最后一层不经历激活函数
    # 就是按照上面的图片中的公式写的
    grades["dz"+str(layers)] = al - y
    grades["dw"+str(layers)] = grades["dz"+str(layers)].dot(caches["a"][layers-1].T) /m
    grades["db"+str(layers)] = np.sum(grades["dz"+str(layers)],axis = 1,keepdims = True) /m
    # 前面全部都是sigmoid激活
    for i in reversed(range(1,layers)):
        grades["dz"+str(i)] = parameters["w"+str(i+1)].T.dot(grades["dz"+str(i+1)]) * sigmoid_prime(caches["z"][i])
        grades["dw"+str(i)] = grades["dz"+str(i)].dot(caches["a"][i-1].T)/m
        grades["db"+str(i)] = np.sum(grades["dz"+str(i)],axis = 1,keepdims = True) /m
    return grades   

# 就是把其所有的权重以及偏执都更新一下
def update_grades(parameters,grades,learning_rate):
    layers = len(parameters)//2
    for i in range(1,layers+1):
        parameters["w"+str(i)] -= learning_rate * grades["dw"+str(i)]
        parameters["b"+str(i)] -= learning_rate * grades["db"+str(i)]
    return parameters
# 计算误差值
def compute_loss(al,y):
    return np.mean(np.square(al-y))

# 加载数据
def load_data():
    """
    加载数据集
    """
    x = np.arange(0.0,1.0,0.01)
    y =20* np.sin(2*np.pi*x)
    # 数据可视化
    plt.scatter(x,y)
    return x,y
#进行测试
x,y = load_data()
x = x.reshape(1,100)
y = y.reshape(1,100)
plt.scatter(x,y)
parameters = init_parameters([1,25,1])
al = 0
for i in range(4000):
    caches,al = forward(x, parameters)
    grades = backward(parameters, caches, al, y)
    parameters = update_grades(parameters, grades, learning_rate= 0.3)
    if i %100 ==0:
        print(compute_loss(al, y))
plt.scatter(x,al)
plt.show()

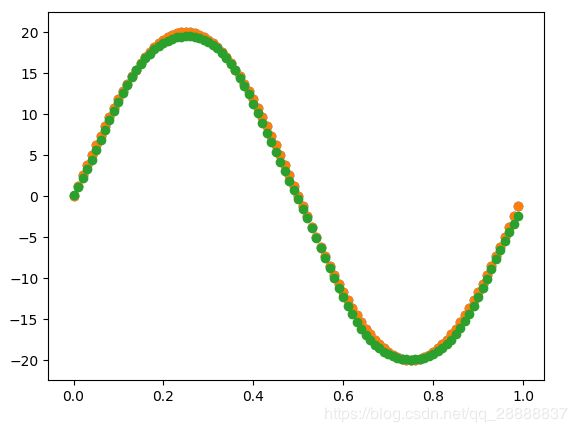
结果显示：

从结果可以看出来几乎能对一条非线性线进行完全拟合了。

参考：

https://blog.csdn.net/qq_28888837/article/details/82901011
https://mooc.study.163.com/learn/2001281002?tid=2001392029#/learn/content?type=detail&id=2001702020&cid=2001700045

欢迎大家关注我的微信公众号，未来上面会推送python 机器学习 算法学习 深度学习 论文阅读 以及偶尔的小鸡汤等内容。ようこそいらっしゃい！

搜索 coderwangson 关注