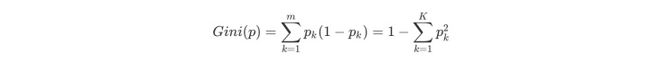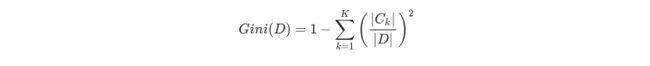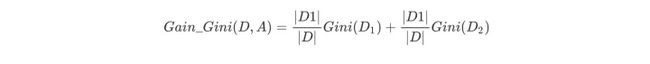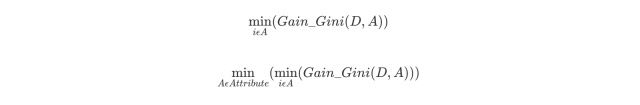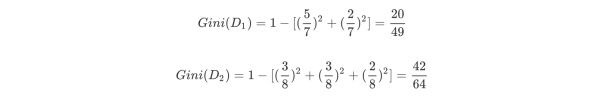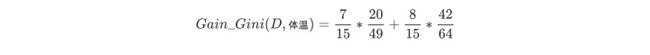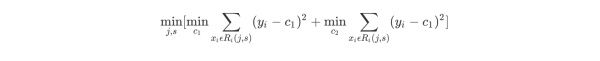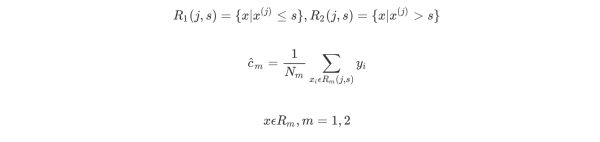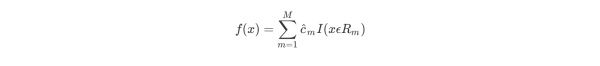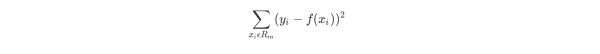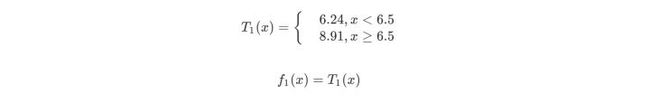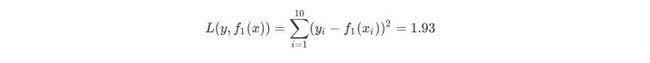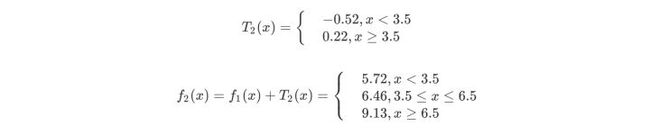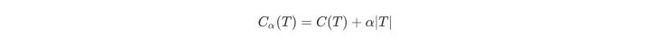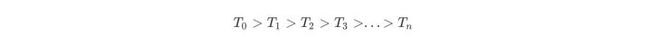CART

1.CART简介

CART是一棵二叉树，每一次分裂会产生两个子节点。CART树分为分类树和回归树。

分类树主要针对目标标量为分类变量，比如预测一个动物是否是哺乳动物。

回归树针对目标变量为连续值的情况，比如预测一个动物的年龄。

如果是分类树，将选择能够最小化分裂后节点GINI值的分裂属性；

如果是回归树，选择能够最小化两个节点样本方差的分裂属性。CART跟其他决策树算法一样，需要进行剪枝，才能防止算法过拟合从而保证算法的泛化性能。

2.CART分类树

2.1算法详解

CART分类树预测分类离散型数据，采用基尼指数选择最优特征，同时决定该特征的最优二值切分点。分类过程中，假设有K个类，样本点属于第k个类的概率为Pk，则概率分布的基尼指数定义为

根据基尼指数定义，可以得到样本集合D的基尼指数，其中Ck表示数据集D中属于第k类的样本子集。

如果数据集D根据特征A在某一取值a上进行分割，得到D1,D2两部分后，那么在特征A下集合D的基尼系数如下所示。其中基尼系数Gini(D)表示集合D的不确定性，基尼系数Gini(D,A)表示A=a分割后集合D的不确定性。基尼指数越大，样本集合的不确定性越大。

对于属性A，分别计算任意属性值将数据集划分为两部分之后的Gain_Gini，选取其中的最小值，作为属性A得到的最优二分方案。然后对于训练集S，计算所有属性的最优二分方案，选取其中的最小值，作为样本及S的最优二分方案。

2.1实例详解

针对上述离散型数据，按照体温为恒温和非恒温进行划分。其中恒温时包括哺乳类5个、鸟类2个，非恒温时包括爬行类3个、鱼类3个、两栖类2个，如下所示我们计算D1,D2的基尼指数。

然后计算得到特征体温下数据集的Gini指数，最后我们选择Gain_Gini最小的特征和相应的划分。

 

3.CART回归树

3.1算法详解

CART回归树预测回归连续型数据，假设X与Y分别是输入和输出变量，并且Y是连续变量。在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树。

 

 

选择最优切分变量j与切分点s：遍历变量j，对规定的切分变量j扫描切分点s，选择使下式得到最小值时的(j,s)对。其中Rm是被划分的输入空间，cm是空间Rm对应的固定输出值。

 

 用选定的(j,s)对，划分区域并决定相应的输出值

 

 继续对两个子区域调用上述步骤，将输入空间划分为M个区域R1,R2,…,Rm，生成决策树。

 

 当输入空间划分确定时，可以用平方误差来表示回归树对于训练数据的预测方法，用平方误差最小的准则求解每个单元上的最优输出值。

 

3.2实例详解

 

 

 

考虑如上所示的连续性变量，根据给定的数据点，考虑1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5切分点。

对各切分点依次求出R1,R2,c1,c2及m(s)，例如当切分点s=1.5时，得到R1={1},R2={2,3,4,5,6,7,8,9,10}，其中c1,c2,m(s)如下所示。

依次改变(j,s)对，可以得到s及m(s)的计算结果，如下表所示。

当x=6.5时，此时R1={1,2,3,4,5,6},R2={7,8,9,10},c1=6.24,c2=8.9。回归树T1(x)为

然后我们利用f1(x)拟合训练数据的残差，如下表所示

用f1(x)拟合训练数据得到平方误差

第二步求T2(x)与求T1(x)方法相同，只是拟合的数据是上表的残差。可以得到

用f2(x)拟合训练数据的平方误差

继续求得T3(x)、T4(x)、T5(x)、T6(x)，如下所示

用f6(x)拟合训练数据的平方损失误差如下所示，假设此时已经满足误差要求，那么f(x)=f6(x)便是所求的回归树。

4.CART剪枝

代价复杂度剪枝算法：

我们将一颗充分生长的树称为T0 ，希望减少树的大小来防止过拟化。但同时去掉一些节点后预测的误差可能会增大，那么如何达到这两个变量之间的平衡则是问题的关键。因此我们用一个变量α 来平衡，定义损失函数如下

• T为任意子树，|T|为子树T的叶子节点个数。
• α是参数，权衡拟合程度与树的复杂度。
• C(T)为预测误差，可以是平方误差也可以是基尼指数，C(T)衡量训练数据的拟合程度。

那么我们如何找到这个合适的α来使拟合程度与复杂度之间达到最好的平衡呢？准确的方法就是将α从0取到正无穷，对于每一个固定的α，我们都可以找到使得Cα(T)最小的最优子树T(α)。

• 当α很小的时候，T0 是这样的最优子树.
• 当α很大的时候，单独一个根节点就是最优子树。

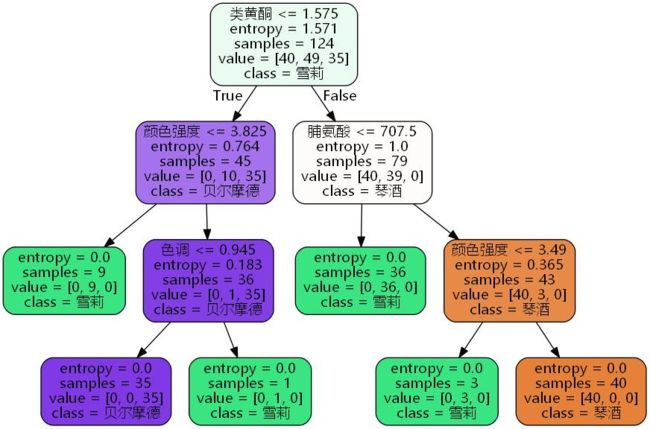
尽管α的取值无限多，但是T0的子树是有限个。Tn是最后剩下的根结点，子树生成是根据前一个子树Ti，剪掉某个内部节点后，生成Ti+1。然后对这样的子树序列分别用测试集进行交叉验证，找到最优的那个子树作为我们的决策树。子树序列如下

因此CART剪枝分为两部分，分别是生成子树序列和交叉验证。

5.sklearn

import pandas as pd
from sklearn import tree
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) #返回预测的准确度accuracy

score

feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']

import graphviz
dot_data = tree.export_graphviz(clf, out_file=".\Tree.dot"
                                ,feature_names = feature_name
                                ,class_names=["琴酒","雪莉","贝尔摩德"]
                                ,filled=True
                                ,rounded=True
                               ) 

 

import re
# 打开 dot_data.dot，修改 fontname="支持的中文字体"
f = open("./Tree.dot", "r+", encoding="utf-8")
open('./Tree_utf8.dot', 'w', encoding="utf-8").write(re.sub(r'fontname=helvetica', 'fontname="Microsoft YaHei"', f.read()))
f.close()

cmd:

dot -Tjpg Tree.dot -o tree.jpg