Python-Tensorflow-二次代价函数、交叉熵、对数似然代价函数、交叉熵应用

一、二次代价函数

 

y代表实际值，其实就是label。y-a即误差，误差的平方和除以样本数。

第二个公式是表示只有一个样本时的代价函数。σ（）是激活函数，输出前需要经过一个激活函数。W是权值，X是上一层的信号值，b是偏置值，最终得到z，z是信号的总和。

第一个式子：对w权值求偏导；（复合函数求偏导）

第二个式子：对b偏置值求偏导。

其中，z表示神经元的输入，sigma表示激活函数。w和b的梯度跟激活函数的梯度成正比，w和b的大小天正得越快，训练收敛得越快。

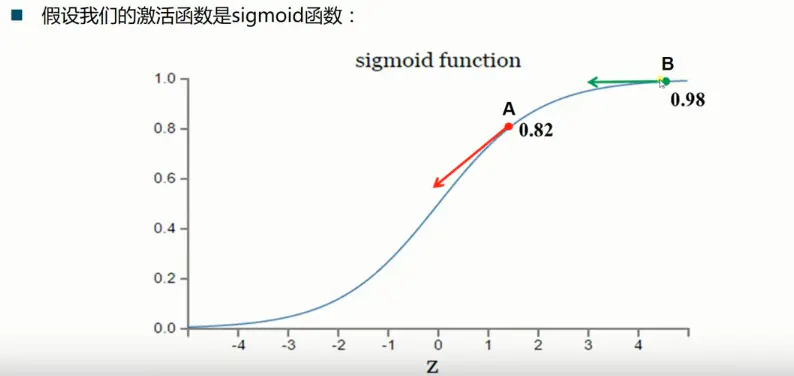
sigmoid函数即S形函数，值域为[0,1]。在B点出现梯度消失。

假设我们的目标是收敛到1，A点的值为0.82离目标比较远，梯度比较大，权值调整比较大。B的值为0.98离目标比较近，梯度比较小，权值调整比较小。调整方案合理。

假设我们的目标是收敛到0，A点的值为0.82离目标比较远，梯度比较大，权值调整比较大，调整方案合理。B的值为0.98，梯度比较小，权值调整比较小，调整方案不合理。

二、交叉熵代价函数

策略更加合理，故相比于二次代价函数，模型收敛更快。

三、对数似然代价函数

与softmax函数搭配使用。softmax函数是将数值转化为概率。

策略更加合理，故相比于二次代价函数，模型收敛更快。

四、优化代价函数的实战训练

这里仅仅将代价函数进行转换，使用softmax较适用的交叉熵代价函数 

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
#读取mnist数据集 如果没有则会下载
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

#每个批次的大小
batch_size = 100
#计算一共有多少批次
n_batch = mnist.train.num_examples // batch_size

#定义两个占位符
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])

#创建简单的神经网络
#群值
W = tf.Variable(tf.zeros([784,10]))
#偏置值
b = tf.Variable(tf.zeros([10]))
#预测值
prediction = tf.nn.softmax(tf.matmul(x,W)+b)

#二次代价函数
#loss = tf.reduce_mean(tf.square(y-prediction))
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.3).minimize(loss)
#初始化变量
init = tf.global_variables_initializer()

#预测数据与样本比较，如果相等就返回1 求出标签
#结果存放在布尔型列表中
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

#进行训练
with tf.Session() as sess:
    sess.run(init)
    for i in range(21):#周期
        for batch in range(n_batch):#批次
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})

        acc = sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
        print("周期 ："+ str(i) + "准确率：" +  str(acc))

运行结果 

周期 ：0准确率：0.8839
周期 ：1准确率：0.9017
周期 ：2准确率：0.9059
周期 ：3准确率：0.9107
周期 ：4准确率：0.9127
周期 ：5准确率：0.915
周期 ：6准确率：0.9155
周期 ：7准确率：0.919
周期 ：8准确率：0.9178
周期 ：9准确率：0.9196
周期 ：10准确率：0.9204
周期 ：11准确率：0.9222
周期 ：12准确率：0.9215
周期 ：13准确率：0.9224
周期 ：14准确率：0.9219
周期 ：15准确率：0.9222
周期 ：16准确率：0.9217
周期 ：17准确率：0.923
周期 ：18准确率：0.9236
周期 ：19准确率：0.9237
周期 ：20准确率：0.9249

通过对比可以看出后者的训练的速度更快，训练的准确率更高了