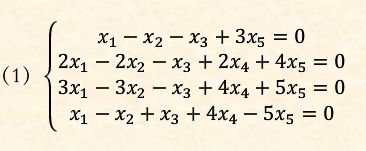Matlab基础(笔记)
文章目录
- 一 MATLAB概述
- 1、简介
- 2、特性
- 3、组成
- 4、功能
- 二 矩阵与阵列
- 1、变量及其操作
- (1)命名规则
- (2)赋值语句
- (3)运算符和表达式
- 2、矩阵产生与表示
- (1)直接输入法创建矩阵
- (2)向量法创建矩阵
- (3)函数法创建矩阵
- 3、矩阵元素的引用
- (1)、矩阵单个元素与行、列提取
- (2)向量标识方法
- 4、矩阵基本操作
- (1)矩阵提取子块、合并短阵、转置与展开
- (2)矩阵的修改和删除
- 5、数组运算
- (1)数组的定义
- (2)数组的数学计算
- (3)数组的关系和逻辑运算
- 三 线性代数
- 1、矩阵代数运算
- 2、矩阵逻辑运算
- 3、逆矩阵
- 引言
- 逆矩阵函数
- 4、行列式与秩
- 5、矩阵特征值及特征向量
- 6、矩阵变换及分解
- 矩阵变换
- 矩阵线性分解
- 7、线性方程组求解
- 四 数据可视化
- 1、二维曲线绘图的基本操作
- (1)直角坐标绘图plot(),stem()
- (2)极坐标绘图 polar()
- (3)对数坐标绘图semilogx(),semilogy(),loglog()
- (4)多重曲线绘图
- 2、图的修饰与分割
- (1)线型、颜色与标记
- (2)坐标轴调整axis()
- (3)设置标题、坐标轴、网格及注释title,xlabel,ylabel,grid on,grid off,legend
- (4)图形填充及颜色fill()
- (5)图形重印 hold
- (6)图形窗口分割subplot()
- 3、特殊二维图形绘制
- 4、三维曲线绘制
- (1)绘制一条三维曲线plot3()
- (2)绘制多条三维曲线
- 5、三维曲面绘图
- (1)创建网格数据meshgrid()
- (2)绘制三维网格曲面mesh,meshc,meshz()
- (3)绘制三维阴影曲面surf,surfc,surfl()
- 五 MATLAB编程基础
- 1、M文件
- Matlab命令的执行方式
- M文件
- 3、函数文件
一 MATLAB概述
1、简介
MATLAB是MathWorks公司推出的一套高性能数值分析计算软件。它将矩阵运算、数值分析、图形处理、编程技术等集成一体,为广大科研人员提供了一个强大的分析、计算、程序设计与仿真的工具,是科学计算最佳平台。
2、特性
口强大的计算功能
口编程语言简单、内涵丰富
口强大的2D、3D数据可视化功能
口丰富的工具箱
口强大的扩展能力、可开发功能
3、组成
MATLAB本身就是一个极其丰富的资源库,MATLAB产品由若干模块组成,不同的模块完成不同的功能,功能模块
示意图如下: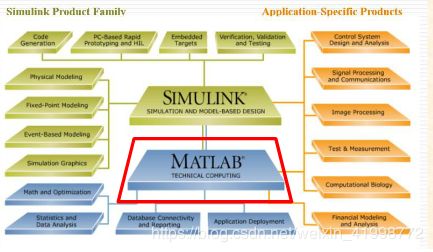
4、功能
·数值分析
·数值和符号计算
·工程与科学绘图
·控制系统的设计与方针
·数字图像处理
·数字信号处理
·通讯系统设计与仿真
·财务与金融工程
二 矩阵与阵列
1、变量及其操作
(1)命名规则
◆变量名第一个字母必须是英文字母。
◆变量名、函数名对字母的大小写是敏感的。如myVar与myvar表示两个不同的变量。
◆变量名可以包含英文字母、下划线和数字。
◆变量名不能包含空格、标点。
◆变量名最多可包含63个字符(6.5及以后的版本)
(2)赋值语句
变量 = 表达式
(3)运算符和表达式
>> a=3;b=2
b =
2
>> a+b
ans =
5
示例2
>> a=[1 4 5;2 6 5;3 6 9]
a =
1 4 5
2 6 5
3 6 9
>> a.^2#每个元素的平方
ans =
1 16 25
4 36 25
9 36 81
>> a*a
ans =
24 58 70
29 74 85
42 102 126
2、矩阵产生与表示
(1)直接输入法创建矩阵
通过键入矩阵中每个元素的值来建立并输入一个矩阵,只须以左方括号开始以逗号或空格为间隔输人元素值,行与行之间用分号隔开,最后以右方括号结尾即可。当矩阵中的元素个数比较少时,这种方法非常适用。
示例3:创建3*3数值矩阵和字符矩阵b
>> a=[1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> b="string"
b =
"string"
(2)向量法创建矩阵
向量可以由冒号和数字产生。其格式为:
向量名=初值:增量:终值
当矩阵中的元素很多且有规律时,则可以通过向量来建立一个矩阵。其基本格式为:
矩阵名=向量
示例4:建立一个10以内的奇数矩阵
>> a = 1:2:10
a =
1 3 5 7 9
(3)函数法创建矩阵
利用内部语句和函数还可以快速产生一些特别有用的矩阵,如单位矩阵随机矩阵、零矩阵等,如表所示。

示例5:建立空矩阵a、单位矩阵b、常数矩阵c、均匀分布随机矩阵d、正态分布的随机矩阵e、零矩阵f。
>> a = []
a =
[]
>> b = eye(3,4)
b =
1 0 0 0
0 1 0 0
0 0 1 0
>> c = ones(3,4)
c =
1 1 1 1
1 1 1 1
1 1 1 1
>> d = rand(4,5)
d =
0.8147 0.6324 0.9575 0.9572 0.4218
0.9058 0.0975 0.9649 0.4854 0.9157
0.1270 0.2785 0.1576 0.8003 0.7922
0.9134 0.5469 0.9706 0.1419 0.9595
>> e = randn(5)
e =
0.6715 1.0347 0.8884 1.4384 -0.1022
-1.2075 0.7269 -1.1471 0.3252 -0.2414
0.7172 -0.3034 -1.0689 -0.7549 0.3192
1.6302 0.2939 -0.8095 1.3703 0.3129
0.4889 -0.7873 -2.9443 -1.7115 -0.8649
>> f = zeros(3)
f =
0 0 0
0 0 0
0 0 0
3、矩阵元素的引用
(1)、矩阵单个元素与行、列提取
MATLAB允许用户对一个矩阵的单个元素进行操作,可以通过元素的下标进行(行、列的序号是从1开始的),修改某些元素的值不会影响其他元素的值。
示例6:单个元素与行、列提取
>> a = [1 2 3;2 3 4;3 4 5;4 5 6]
a =
1 2 3
2 3 4
3 4 5
4 5 6
>> a(2,3)%提取第2行第三列元素,用逗号隔开行列
ans =
4
>> a(2:3,:)%提取a矩阵的2,3行;其中冒号表示从某行(列)到某行(列),只一个冒号表示全部行或列
ans =
2 3 4
3 4 5
>> a(:,1:2)%提取a矩阵的1,2列
ans =
1 2
2 3
3 4
4 5
(2)向量标识方法
**向量标识方式A(vr,vc)**,这种标识方式特别有用。令vr=[i1,i2....ik]、vc=[j1,j2...jn]分别是含有矩阵A的行号和列号的单调向量,A(vr,vc)是 取出矩阵A的第i1,i2....ik行与j1,j2....jn列**交叉处的元素所构成的新矩阵**
示例7:向量标识方法构成新矩阵
>> a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> vr= [1,3]
vr =
1 3
>> vc = [2,3]
vc =
2 3
>> b = a(vr,vc)%取出a矩阵的1,3行和2,3列组成新的矩阵b
b =
2 3
8 9
4、矩阵基本操作
(1)矩阵提取子块、合并短阵、转置与展开
提取子块:提取矩阵的某一部分,可以使用冒号表达式。在MATLAB中,冒号“:”表示“全部”
示例8:输入一个4*3的a矩阵,选出前三行构成一个新矩阵b,再选出前两列构成另一个矩阵c
>> a=[ 1 2 3;4 5 6;7 8 9;10 11 12]
a =
1 2 3
4 5 6
7 8 9
10 11 12
>> b=a(1:3,:)
b =
1 2 3
4 5 6
7 8 9
>> c=a(:,1:2)
c =
1 2
4 5
7 8
10 11
矩阵合并
把两个矩阵合并成一个大矩阵 C=[A;B]
矩阵的转置
用符号”’”(单引号)可 以进行矩阵的转置运算。
矩阵的展开
矩阵的展开是按照矩阵在内存中的实际存放形式展开的。矩阵的元素在内存中是按列存放的,即先存放第一列,接着存放第二列…把一个矩阵内的所有元素统一展开成一个列向量,其指令格式为:B=A(:)
示例9:把矩阵A[ 1 3 5;7 9 11]和矩阵B[2 4 6]合并成一个矩阵,再转置后展开
>> A = [ 1 3 5;7 9 11]
A =
1 3 5
7 9 11
>> B=[2 4 6]
B =
2 4 6
>> C=[A;B]%矩阵合并
C =
1 3 5
7 9 11
2 4 6
>> D=C'%矩阵转置
D =
1 7 2
3 9 4
5 11 6
>> E=D(:)%矩阵展开
E =
1
3
5
7
9
11
2
4
6
(2)矩阵的修改和删除
矩阵的修改:要修改已经定义好的矩阵,只需对它的元素或子块重新赋值就可以了。
矩阵的删除:删除矩阵的行或列:可以用将矩阵某行或某列赋值为空值[]的方法,而直接删除此行或此列,删除行或列的部分元素则会出错。
示例10
>> a=rand(3)
a =
0.4898 0.7094 0.6797
0.4456 0.7547 0.6551
0.6463 0.2760 0.1626
>> a(1,:) = [0 0 0]%将第一行修改为0
a =
0 0 0
0.4456 0.7547 0.6551
0.6463 0.2760 0.1626
>> a(1:2,:) = []%删除第1,2行
a =
0.6463 0.2760 0.1626
5、数组运算
(1)数组的定义
在数学上,一维数组相当于一个只有一行或一列的矩阵.因此我们要定义数组也就是定义一个1n或n1的矩阵。对于二维数组而言,用矩阵的形式存储也是最为方便的
(2)数组的数学计算
和矩阵一样,数组也有加减乘除运算。
示例11
>> a=[1 2 3;5 6 7]
a =
1 2 3
5 6 7
>> b=[4 5 6;8 9 0]
b =
4 5 6
8 9 0
>> a+b %数组加法运算
ans =
5 7 9
13 15 7
>> a.*b %数组乘法运算:".*"
ans =
4 10 18
40 54 0
>> a.^3 %数组乘方运算:".^"
ans =
1 8 27
125 216 343
>> a./b %用a中元素除以b中的相应元素
ans =
0.2500 0.4000 0.5000
0.6250 0.6667 Inf
>> a.\b %用b中元素除以a中相应元素
ans =
4.0000 2.5000 2.0000
1.6000 1.5000 0
(3)数组的关系和逻辑运算
在MATLAB中,所有的关系运算和逻辑运算都是按数组运算规则定义的。
数组关系运算
MATLAB提供了下列关系运算符来实现两个量之间的比较:< 小于 >大于
<=小于等于 >=大于等于
==等于 ~=不等于
在关系运算中,当关系成立时结果为1(真),不成立时结果为0(假)。
示例12
>> a=[1 2 3;5 6 7]
a =
1 2 3
5 6 7
>> b=[4 5 6;8 9 0]
b =
4 5 6
8 9 0
>> a<=b %比较a和b的对应元素
ans =
2×3 logical 数组
1 1 1
1 1 0
数组逻辑运算
MATLAB提供的逻辑运算符有三种:
&与,|或,~非
在逻辑运算中,只有非零(1)和0两种元素。
示例13
>> a=[2 3 0]
a =
2 3 0
>> b=[0 1 2]
b =
0 1 2
>> a&b
ans =
1×3 logical 数组
0 1 0
>> ~a
ans =
1×3 logical 数组
0 0 1
>> ~b
ans =
1×3 logical 数组
1 0 0
>> a|b
ans =
1×3 logical 数组
1 1 1
三 线性代数
1、矩阵代数运算
(1)加法运算:各元素对应相加,如果矩阵与一常数(标量)相加,则把该常数看成是同阶的矩阵。
>> a=[1 2 3]
a =
1 2 3
>> a+5
ans =
6 7 8
(2)减法运算:各元素对应相减,如果矩阵与一常数(标量)相减,则把该常数看成是同阶的矩阵。
注意:与加法运算相同,只有维数相同的矩阵才能进行加、减法运算。
(3)乘法运算
运算符:*
运算规则:按照线性代数中矩阵乘法的操作运算,即前面矩阵各行元素分别与后面矩阵各列元素相乘并相加。矩阵与常数相乘等于每个元素乘以该常数

注意:只有当两个矩阵中前-一个矩阵的列数和后一个矩阵的行数相同时,才可以进行乘法运算。
(4)点乘运算
运算符:.*
运算规则:按照线性代数中矩阵点乘法的操作运算,即两个维数相同矩阵对应元素相乘。矩阵与常数点乘和矩阵与常数相乘结果相等,也等于每个元素乘以该常数。
注意:使用"."相乘的两个矩阵阶数应相同。
(5)矩阵除法运算
运算符:\(矩阵左除)和/(矩阵右除)
运算规则:左除和右除用于方程求解时,一般来说,
X=A\b是方程AX=b的解
X=b/A是方程X*A=b的解。
矩阵除以常数,等于每个元素除以常数,只能用普通除法“/”,不用“\”
(6)矩阵点除运算
运算符:./、.
运算法则:A./B是A各元素除以B中各元素。
A.\B=B./A
(7)矩阵乘方运算
运算符:^
运算法则:当A为方阵、P为大于0的整数时,AP表示A的p次方,即A白乘P次;当P为小于0的整数时,AP表示A-1的IPI次方。(乘方是乘法的扩充,为保证合法性,要求矩阵为方阵)
(8)矩阵点乘方运算
运算符:.^
运算法则:A.^B表示矩阵A中元素对矩阵B中的对应元素求幂次方,其中A.B两个矩阵的维度必须一致。结果矩阵的维度与A.B矩阵的维度相同。
矩阵的单个数点乘方A."P表示矩阵A中每个元素对P这个数字求幂次方。


2、矩阵逻辑运算
(1)关系运算符
MATLAB共有6种关系运算符用于关系运算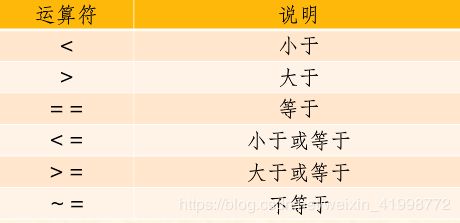
关系运算符的运算法则
1、当两个标量进行比较时,直接比较两数大小。若关系成立,结果为1,否则为0。
2、当两个维数相等的矩阵进行比较时,其相应位置的元素按标量关系进行比较,并给出结果,形成一个维数与原来相同的0、1矩阵。
3、当一个标量与一个矩阵比较时,该标量与矩阵的各元素进行比较,结果形成一个与矩阵维数相等的01矩阵。

(2)逻辑运算符

逻辑运算的方法与关系运算相类似,都是对同阶矩阵中的对应元素进行逻辑运算,如果其中一个是标量,则标量逐个与矩阵中的每一个元素进行逻辑运算。
(3)其他关系和逻辑函数


3、逆矩阵
引言
在工程实际中需要求解大量矩阵的逆矩阵。虽然大多数方程组都是非线性的,但一般都可以通过一定的变换转化为线性方程组,矩阵求逆往往与线性代数方程的求解有关,因此本节将着重讨论矩阵求逆。

由上述的引入我们可以将逆矩阵定义为:设a为n阶矩阵,若存在n阶矩阵b,使得ab=ba=E,则称矩阵a是可逆的,矩阵b称为a的逆矩阵。
![]()
注意:唯一性:若a是可逆矩阵,则a的逆矩阵是唯一的。
逆矩阵函数
在MATLAB中提供了一个计算逆矩阵的函数C=inv(),调用方法如下:
C = inv(A)
通过该函数的调用就可以直接由给定的A矩阵求出逆矩阵C来。但是inv()函数的调用也有需要注意的地方,如果A矩阵为奇异或接近奇异,则利用此函数有可能产生错误的结果。
注意事项:矩阵的逆矩阵并不总是存在。如果矩阵的行列式为零,则不存在逆矩阵。此时可以调用pinv0函数求矩阵的伪逆。
>> b =[1 2 3;4 5 6;7 8 9]
b =
1 2 3
4 5 6
7 8 9
>> inv(b)
警告: 矩阵接近奇异值,或者缩放错误。结果可能不准确。RCOND = 2.202823e-18。
ans =
1.0e+16 *
0.3153 -0.6305 0.3153
-0.6305 1.2610 -0.6305
0.3153 -0.6305 0.3153
>> pinv(b)
ans =
-0.6389 -0.1667 0.3056
-0.0556 0.0000 0.0556
0.5278 0.1667 -0.1944
4、行列式与秩
(1)计算行列式
MATLAB提供了计算矩阵行列式的内部函数,使用方法如下:
det(a)
注:其中a为n阶方阵。
对于数值矩阵,直接调用即可;
对于字符型矩阵,需要声明变量
(2)计算秩
矩阵中线性无关的列向量个数称为列秩,线性无关的行向量个数称为行秩。可以证明列秩与行秩是相等的。
MATLAB中用函数
rank()
来计算矩阵得秩。
5、矩阵特征值及特征向量
引言:
矩阵的特征值与特征向量是矩阵的数字特征,利用矩阵的特征值与特征向量可判断矩阵的相似、解决矩阵对角化及矩阵正交化等问题,促进了矩阵理论的进一步的发展及应用。
定义:
设A是n阶矩阵,如果存在数入和n维非零列向量X满足:
AX=λX
则称λ为A的特征值,称向量X为A的对应于特征值λ的特征向量。
![]()
注意:
1、矩阵λE-A称为A的特征矩阵;
2、λ的n次多项式|λE-A|称为A的特征多项式;
3、方程|λE-A|=0称为A的特征方程。
函数介绍
MATLAB中计算矩阵a的特征值和特征向量的函数是eig(a),常见的有以下两种用法:
(1)E=eig(a):求矩阵a的全部特征值,构成向量E;
(2)[V,D]=eig(a):求矩阵a的全部特征值,构成对角阵D,并求a的特征向量构成V的列向量。
>> a=[1 2 2;1 -1 1;4 -12 1]
a =
1 2 2
1 -1 1
4 -12 1
>> E=eig(a)
E =
1.0000 + 0.0000i
-0.0000 + 1.0000i
-0.0000 - 1.0000i
>> [V,D]=eig(a)
V =
0.9045 + 0.0000i -0.7255 + 0.0000i -0.7255 + 0.0000i
0.3015 + 0.0000i -0.2176 - 0.0725i -0.2176 + 0.0725i
-0.3015 + 0.0000i 0.5804 - 0.2902i 0.5804 + 0.2902i
D =
1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 - 1.0000i
6、矩阵变换及分解
矩阵变换

示例:建立一个3×3的魔方矩阵,提取其对角元素和下三角矩阵,并上下翻转。
>> a=magic(3) %建立魔方矩阵
a =
8 1 6
3 5 7
4 9 2
>> a_diag=diag(a) %提取对角元素
a_diag =
8
5
2
>> a_tril=tril(a) %提取下三角矩阵
a_tril =
8 0 0
3 5 0
4 9 2
>> a_flipud=flipud(a) %上下翻转
a_flipud =
4 9 2
3 5 7
8 1 6
矩阵线性分解
矩阵分解是把一个大的矩阵分解为几个比较简单的矩阵的乘积。常用的分解方法有一下四种:
(1)Cholesky分解;
cholesky分解是将一个正定对称矩阵分解成一个三角矩阵L和其转置的乘积,即满足L’L=A,其格式如下:L=chol(A)
其中A代表要分解的实对称矩阵。
示例:建立一个4×4的pascal矩阵,进行Cholesky分解。
>> a=pascal(4)
a =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
>> b=chol(a)
b =
1 1 1 1
0 1 2 3
0 0 1 3
0 0 0 1
>> b'*b %验证
ans =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
(2)三角分解法(LU);
三角分解是将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵/的乘积,即满足LU=A。
格式如下:
[L,U]=lu(A)
其中A代表要分解的矩阵,L代表分解后得到的下三角矩阵,U代表分解后得到的上三角矩阵。
示例:对矩阵三阶魔方矩阵进行三角分解。
>> a=magic(3)
a =
8 1 6
3 5 7
4 9 2
>> [c,d]=lu(a)
c =
1.0000 0 0
0.3750 0.5441 1.0000
0.5000 1.0000 0
d =
8.0000 1.0000 6.0000
0 8.5000 -1.0000
0 0 5.2941
>> c*d
ans =
8 1 6
3 5 7
4 9 2
(3)正交分解法(QR);
正交分解是将一个矩阵分解为一个正交矩阵和一个上三角矩阵的乘积。
函数是qr,其格式如下:
[Q,R]=qr(4)
其中A代表要分解的矩阵,Q代表分解后得到的正交矩阵,R代表分解后得到的上三角矩阵。
示例:
>> a=[1 3 5;2 4 6;7 9 11;2 5 8]
a =
1 3 5
2 4 6
7 9 11
2 5 8
>> [Q,R]=qr(a)
Q =
-0.1313 -0.5076 0.8510 0.0304
-0.2626 -0.3610 -0.2249 -0.8661
-0.9191 0.3722 0.0765 0.1037
-0.2626 -0.6881 -0.4684 0.4880
R =
-7.6158 -11.0297 -14.4437
0 -3.0569 -6.1139
0 0 0.0000
0 0 0
(4)奇异值分解法(SVD)
奇异值分解是将一个矩阵分解成三个矩阵的乘积。
![]()
其中U和V分别代表两个正交矩阵,而s代表一对角矩阵。
调用格式:[u,s,v]= sud(A).
注意:U,V为正交矩阵。
即:UU’=E;VV’=E
示例:
>> a=[1 3 5;2 4 6]
a =
1 3 5
2 4 6
>> [u,s,v]=svd(a)
u =
-0.6196 -0.7849
-0.7849 0.6196
s =
9.5255 0 0
0 0.5143 0
v =
-0.2298 0.8835 0.4082
-0.5247 0.2408 -0.8165
-0.8196 -0.4019 0.4082
>> u'*u
ans =
1.0000 -0.0000
-0.0000 1.0000
>> v'*v
ans =
1.0000 -0.0000 -0.0000
-0.0000 1.0000 -0.0000
-0.0000 -0.0000 1.0000
7、线性方程组求解
>> A=[1 2;4 -3]
A =
1 2
4 -3
>> b=[23;2]
b =
23
2
>> X=A\b
X =
6.6364
8.1818
>> a=[1 -1 -1 0 3;2 -2 -1 2 4;3 -3 -1 4 5;1 -1 1 4 -1]
a =
1 -1 -1 0 3
2 -2 -1 2 4
3 -3 -1 4 5
1 -1 1 4 -1
>> B=null(a)
B =
0.8063 0.1865 0.4033
0.5680 -0.4961 -0.5279
-0.1026 -0.7026 0.6141
-0.0623 -0.1104 -0.4127
-0.1136 -0.4617 -0.1057
B的第一列为a1,第二列为a2,第三列为a3,al,a2,a3是方程组的一个基础解系,方程组的通解为x-clal+c2a2+c3*a3,其中c1,c2,c3是任意常数。
四 数据可视化
1、二维曲线绘图的基本操作
(1)直角坐标绘图plot(),stem()
plot指令的基本调用格式
plot(x)
x为向量时,以该元素的下标为横坐标、元素值为纵坐标绘出曲线
示例:
>> y=[0 0.6 2.3 5 8.3 11.7 15 17.7 19.4 20]
y =
1 至 6 列
0 0.6000 2.3000 5.0000 8.3000 11.7000
7 至 10 列
15.0000 17.7000 19.4000 20.0000
>> plot(y)
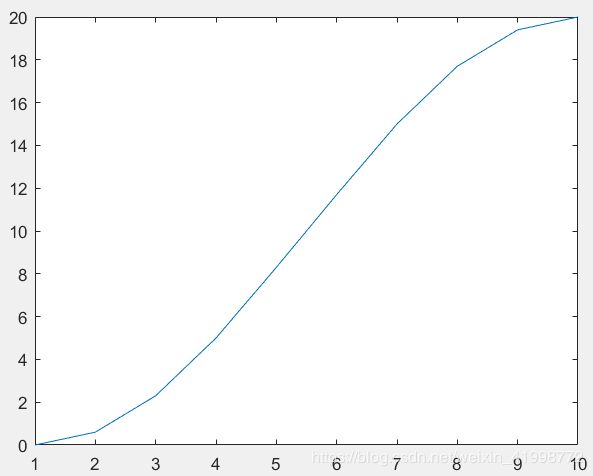
stem()是画离散序列的针状图(火柴棍图)

subplot(312),stem(n,x1,‘filled’,‘k’);
filled表示填充,k表示黑色

plot(x,y)
x、y为同维数组时,绘制以x,y元素为横纵坐标的曲线
示例:
绘制![]()
x=-2*pi:0.05:2*pi;
y=sin(x);
plot(x,y)

plot(x1,y1,x2,y2…)
绘制以x1为横坐标、y1为纵坐标的曲线1,以x2为横坐标、y2为纵坐标的曲线2等。
示例:

x1=-pi:0.05:pi;
x2=0:0.05:pi;
x3=-pi:0.05:2*pi;
y1=sin(x1);
y2=sin(x2).*sin(9*x2);
y3=cos(x3).*sin(x3);
plot(x1,y1,x2,y2,x3,y3)
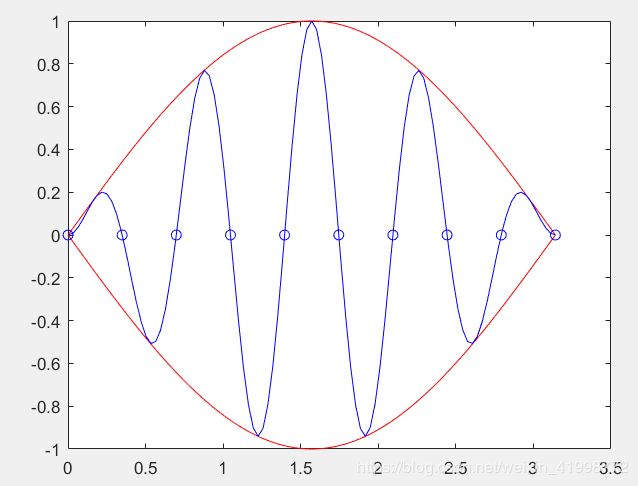
t=(0:pi/100:pi)'; %长度为101的时间采样列向量
y1=sin(t)*[1,-1];%包络线函数,是(101x2)的矩阵
y2=sin(t).*sin(9*t);%长度为101的调制波列向量
t3=pi*(0:9)/9;
y3=sin(t3).*sin(9*t3);
plot(t,y1,'r',t,y2,'b',t3,y3,'bo')
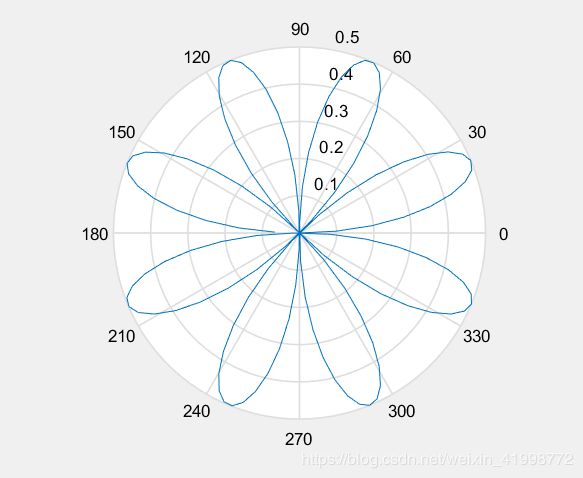
(2)极坐标绘图 polar()
极坐标绘图函数polar,调用格式为polar(theta,tho)
theta,tho分别为角度和半径。
![]()
theta=0:0.05:2*pi;
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho);
(3)对数坐标绘图semilogx(),semilogy(),loglog()
(4)多重曲线绘图
2、图的修饰与分割
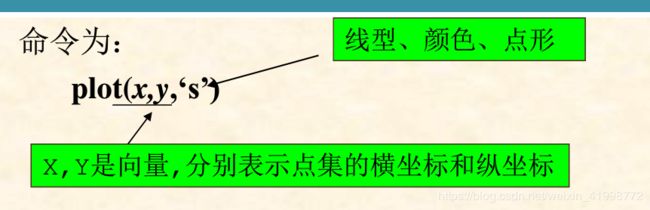
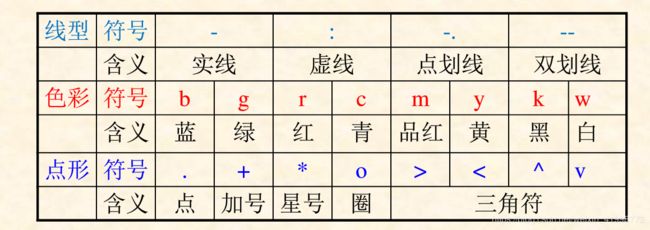
(1)线型、颜色与标记
绘图命令还包含有参数选项时,plot指令的基本调用格式plot(x,y,option)
'option’选项用于指明图形的线型,颜色及标记,便于区分在同一个窗口绘制的多条曲线。
x=0:0.05:2*pi;
y1=sin(x);
y2=sin(2*x+pi/3);
plot(x,y1,'r-+',x,y2,'b:*')
(2)坐标轴调整axis()
可以利用axis命令对所要绘制的图形的坐标轴进行适
调用格式:
axis([xmin xmax ymin ymax])
功能:将所画图形的X轴范围限定在(xmin,xmax),Y轴范围限定在(ymin,ymax)之间,相当于对原图进行放大或缩小处理。
x=0:0.05:2*pi;
y1=sin(x);
y2=sin(2*x+pi/3);
plot(x,y1,'r-+',x,y2,'b:*')
axis([0 2*pi -2 2])
(3)设置标题、坐标轴、网格及注释title,xlabel,ylabel,grid on,grid off,legend
title(str):在所画图形的上端显示该图形标题的字符串str
xlabel(str):将字符串str水平放置在X轴,以说明区轴数据的含义。
**ylabel(str)**将字符串str水平放置在Y轴,以说明Y轴数据的含义。
grid on:在所画图形中添加网格线。
grid off:对已有网格线的图像去掉网格线。
legend(str1,str2…):对图像中的曲线进行注释说明。
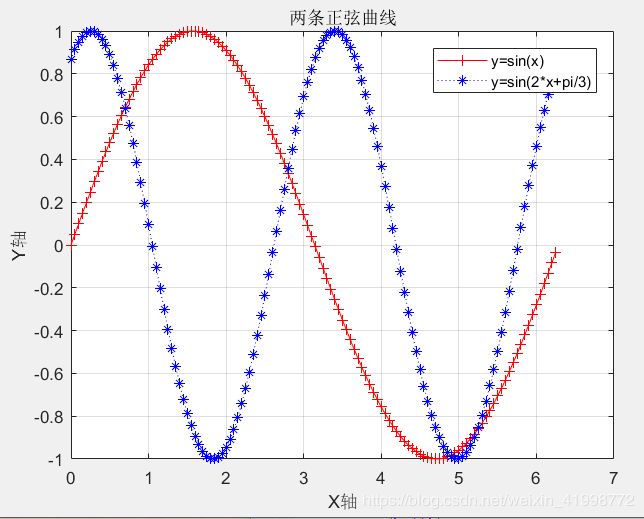
x=0:0.05:2*pi;
y1=sin(x);
y2=sin(2*x+pi/3);
plot(x,y1,'r-+',x,y2,'b:*')
title('两条正弦曲线')
xlabel('X轴')
ylabel('Y轴')
grid on
legend('y=sin(x)','y=sin(2*x+pi/3)')
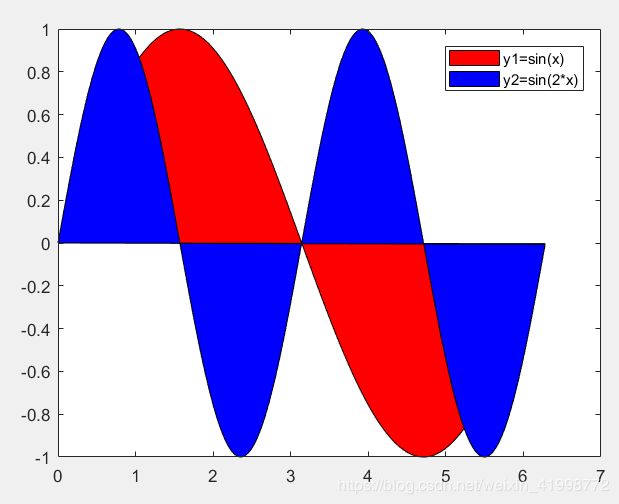
(4)图形填充及颜色fill()
fill(x,y,color)令用于对x,y构成的图形内填充指定颜色

x=0:0.01:2*pi;
y1=sin(x);
y2=sin(2*x);
fill(x,y1,'r',x,y2,'b')
legend('y1=sin(x)','y2=sin(2*x)')
(5)图形重印 hold
(6)图形窗口分割subplot()
subplot用于在一个窗口的不同区域绘制不同图形。
subplot指令的基本调用格式
subplot(m,n,k)的含义:图形窗口包含(mxn)个子图,k为要指定的当前子图的编号。其编号原则:左上方为第1子图,然后向右向下依次排序。该指令按缺省值分割子图区域。
```c
[x,y]=meshgrid(-10:0.1:10);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2)
subplot(121) %121指 共1x2=2个图,此图放到第1位
meshc(x,y,z)
title('含有等高线的草帽面')
subplot(122)%此图放到第2位
meshz(x,y,z)
title('含有底座的草帽面')
3、特殊二维图形绘制
直方图(bar)
离散干图(stem)
饼图(pie)
阶梯图(stairs)
概率分布图(hist)
条形误差图(errorbar)
4、三维曲线绘制
(1)绘制一条三维曲线plot3()
t=0:0.01:10*pi;
x=sin(t);
y=cos(t);
z=t;
plot3(x,y,z,'g+');
title('旋转曲线')
(2)绘制多条三维曲线
plot3(xl,yl,zl,cl,xc2,y2,z2,c2,…)其中x1,y1,z…表示三维坐标向量,c1,c.表示线形或颜色。
5、三维曲面绘图
(1)创建网格数据meshgrid()
格式:[X,Y]=meshgrid(x,y);
功能:由向量x,y产生绘制三维图形所需的网格数据矩阵XY.
说明:x.y代表三维图形在XY轴方向的数据点。XY代表数据网格矩阵。
x=[1 2 3 4 5];
y=[5 6 8 9];
[X,Y]=meshgrid(x,y)
X =
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
Y =
5 5 5 5 5
6 6 6 6 6
8 8 8 8 8
9 9 9 9 9
(2)绘制三维网格曲面mesh,meshc,meshz()
格式:mesh(X,Y,Z);
功能:绘制X,Y为底,Z为函数值的三维网格曲面.
其他调用格式:mesh(Z)
示例:
[x,y]=meshgrid(-10:0.1:10);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2)
mesh(x,y,z)
title('草帽面')
meshz(x,y,z)
绘制带有底座的三维网格曲面
参数调用格式与mesh函数类似。
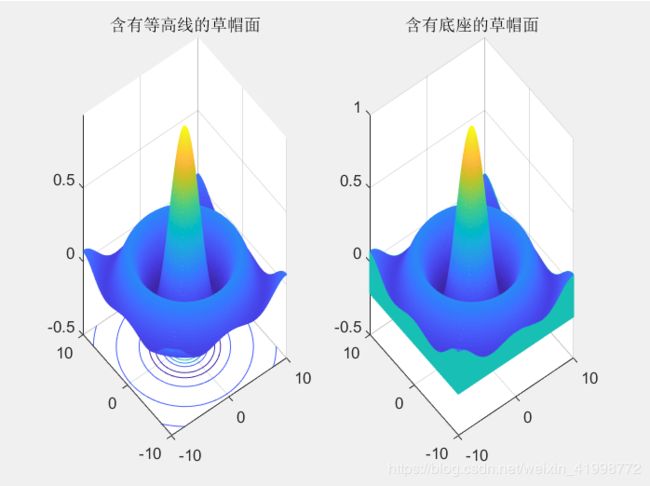
[x,y]=meshgrid(-10:0.1:10);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2)
subplot(121) %121指 共1x2=2个图,此图放到第1位
meshc(x,y,z)
title('含有等高线的草帽面')
subplot(122)%此图放到第2位
meshz(x,y,z)
title('含有底座的草帽面')
(3)绘制三维阴影曲面surf,surfc,surfl()
命令:
surf(x,y,z)功能:绘制一个三维阴影曲面。
surfc(x,y,z)功能:绘制一个带有等高线的三维阴影曲面。
surfl(x,y,z)功能:绘制一个带有光照效果的阴影曲面。
说明:surf命令中提供三种表面颜色的分布方式
Shading faceted:截面式颜色分布;
Shadinginterp:插补式颜色分布;
Shading flat:平面式颜色分布。
五 MATLAB编程基础
1、M文件
Matlab命令的执行方式
(1)交互式命令执行方式(命令窗口)
逐条输入,逐条执行,操作简单、直观,但速度慢,执行过程不能保留。
(2)M文件的程序执行方式
将命令编成程序存储在一个文件中(M文件),依次运行文件中的命令,可以重复进行。
M文件
是由若干Matlab命令组合在一起构成的,它可以完成某些操作,也可以实现某种算法。
分类:
脚本文件(Script File)
函数文件(Function File)
注意:它们的扩展名都是.m
创建方法
(1)菜单操作
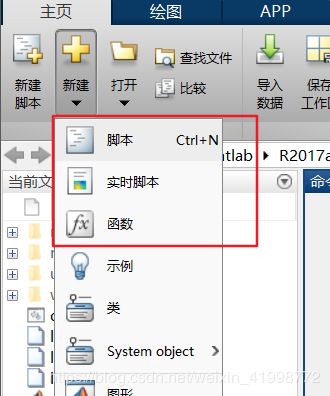
(2)命令操作
在MATLAB命令窗口输入命令edit,启动MATLABX本编辑器后,输入M文件的内容并存盘。

(3)命令按钮操作
示例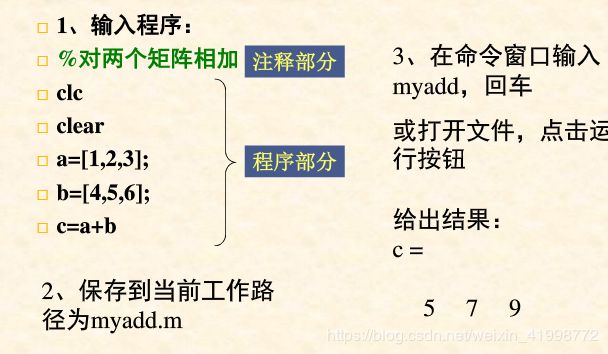

function [s,p] = fcircle( r )
%计算圆的面积和周长
% r半径,s面积,p周长
s=pi*r*r;
p=2*pi*r;
end
命令行窗口
>> fcircle(2)
ans =
12.5664
3、函数文件
函数文件是另一种形式的M文件,每一个函数文件都定义一个函数。
Matlab提供的标准函数大部分是由函数文件定义的。
函数文件由function语句引导,其基本结构为:function 输出形参表=函数名(输入形参表)
注释说明部分
函数体语句
其中,以function开头的一行为引导行,表示该M文件是一个函数文件。
当输出形参多于一个时,应该用方括号括起来。
(1)关于函数名
函数文件名通常由函数名再加上扩展名.m组成。
当函数文件名与函数名不同时,Matlab将忽略函数名而确认文件名因此调用时使用函数文件名。
(2)关分注释说明包括3部分:
①紧随引导行之后以%开头的第一注释行。
这一行一般包括大写的函数文件名和函数功能简要描述,供lookfor关键词查询和help在线帮助时使用。
②第一注释行及之后连续的注释行。
通常包括函数输入/输出参数的含义及调用格式说明等信息,构成全部在线帮助文本。
③与在线帮助文本相隔一空行的注释行。
包括函数文件编写和修改的信息,如作者和版本等。