树和二叉树定义和基本术语

前言：

以下是听老师在网上讲课的笔记总结

一.树的定义和基本术语

1.介绍

树型结构是一类重要的 非线性数据结构 ，元素结点间存在明
显的分支和层次关系。现实世界中，能用树的结构表示的例子
：学校的行政关系、书的层次结构、人类的家族血缘关系等。

2.定义

树（tree） 是 n(n ≥ 0)个结点的有限集合T，T为空时称为
空树，否则满足如下条件:

(1) 有且仅有一个称为 根(root) 的结点;

(2) 其余结点可分为m（m>=0）个互不相交的有限集合T1, T2, …, Tm, 且其中每一个集合本身又是一棵树,称之为根的 子树（subtree）。

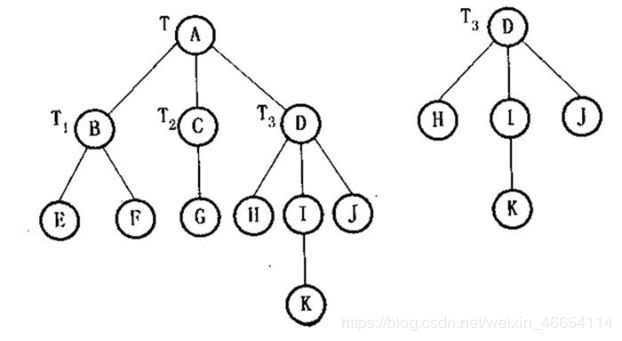
如上图所示，T是有11个结点的树，其中A是根,其余结点分成3个
互不相交的子集:T1={B,E,F},T2={C,G},T3={D,H,I,J,K}；T1、T2和T3都
是根A的子树，且本身也是一棵树

3. 基本术语

1 、结点：包含一个数据元素及若干指向其子树的分支。

2 、边：连接两个结点的线段。

3 、度：一个结点拥有的子树数称为该 结点的度。

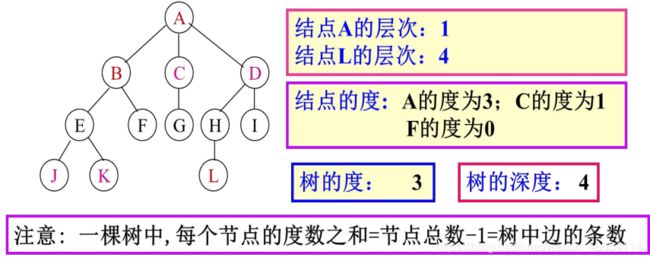
4 、 树的度：指该树中结点的最大度数。例中树A的度为：3

5 、叶子（终端结点）：度为零的结点称为叶子。例：下图j,k,f,G,L,I均为叶子

6 、分支结点（非终端结点）：度不为零的结点。

7 、内部结点：根结点（开始结点）之外的分支结点称为内部
结点。

8 、树的深度（高度）：树中结点的最大层次称为树的深度。

9 、结点的层次：从根开始定义起，根为第一层，根的孩子
为第二层。若某结点在第l层，则其子树的根就在第l+1层

二.二叉树

1. 二叉树的定义

二叉树是n(n>=0)个结点的有限集，它或为空树(n=0)， 或由一个根结点和两棵分别称为左子树和右子树的互不相交的二叉树构成。

2.二叉树的 特点

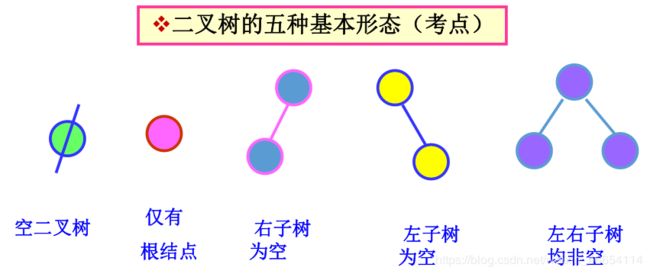
每个结点 至多有两棵子树(即不存在度大于2每个结点 至多有两棵子树(即不存在度大于2的结点), 并且，二叉树的子树有左、右之分，其次序不能任意颠倒。

二叉树有5种基本形态：

3.二叉树的性质

性质1 ：二叉树的第i层上 至多有2 ^(i-1) （i >=1）个结点。

性质2 ：深度为k的二叉树中 至多2^k -1个结点。

性质3 ： 对任何一棵二叉树T ，如果其终端结点数为n ，度
为2 的结点数为N ，则n ＝N＋ 1 。

列：

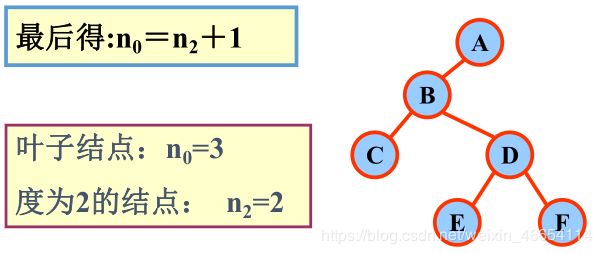
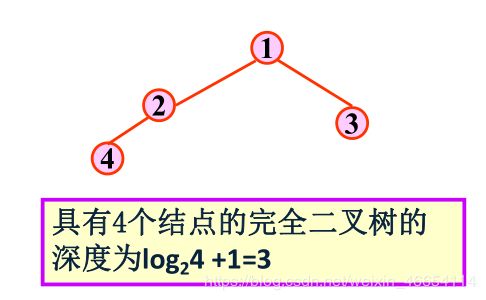
性质4 ： 具有n 个结点的 完全二叉树 的深度k 为 └ log n ┘ +1 。(└ log n ┘的意思是表示最小下限，比如2.5的做小下限是2)

列：

性质5： 如果对一棵有n 个结点的 完全二叉树 （其深度为
└log (n)┘+1 ）的结点按层序编号（从第一层到第└log (n)┘+1 层，
每层从左到右），则对任意结点i(0≤i≤n),有：

1. 如果i=1，则结点i是二叉树的根，无双亲； 若i>1，则它的
   双亲结点的编号为└i/2┘。

2. 若2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左
   孩子编号为2i 。

3 ）若2i+1>n，则结点i无右孩子；否则其右孩子编号为2i+1。

作用： 很容易确定每个结点的父结点、左子和右子结点的位置。

小知识：

完全二叉树可以不满，但是少的结点只能从满二叉树的最下层、最

右边少起。

三.学完就练

1、在一棵度数为4的树T中，若有20个度为4的结点，10
个度为3的结点，1个度为2的结点，10个度为1的结点，
则树T的叶结点个数是（ ）。
A． 41 B．82 C．113 D．122
答案：B 提示：使用性质三的思路，从两个方向

2、一棵完全二叉树上有 1001 个结点，其中叶子结点的
个数是（ ）。
A． 250 B． 501 C．254 D．505

答案：B 考察性质三，和性质五

没有度为1的节点，度为2是500

四.二叉树的存储结构

1. 顺序存储结构 （不常用）

用一组 连续的存储单元存放二叉树中的结点，适用于满二叉树和完全二叉树。

2.链式存储结构(常用)

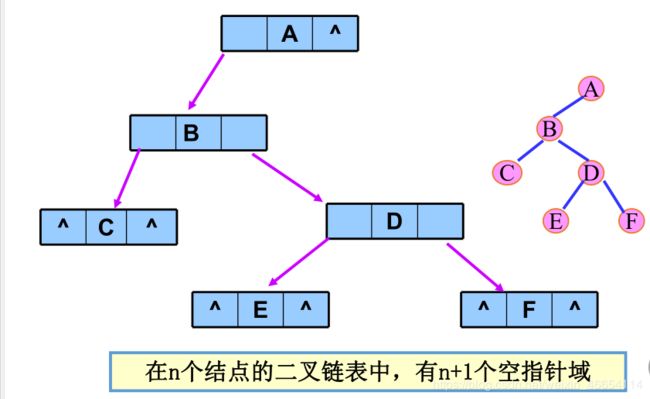
二叉链表：每个结点由数据域、左指针域和右指针域组成。

Typedef struct node{
Datatype data;
Struct node *lchild,*rchild;
}BiTNode;
typedef BiTNode * BinTree ;

注意：BiTNode是结点类型，BinTree是指向BiTNode的指针类型。

三叉链表：增加一个指向其双亲结点的指针域。（不常用）

作者：RodmaChen
本人博客：https://blog.csdn.net/weixin_46654114(关注我，还会持续更新)
qq：1342709867
转载说明：务必联系我，注明来源，附带本人博客连接。谢谢配合。

请给我点个赞鼓励我吧