010-数据结构与算法 栈与队列算法题集训 2
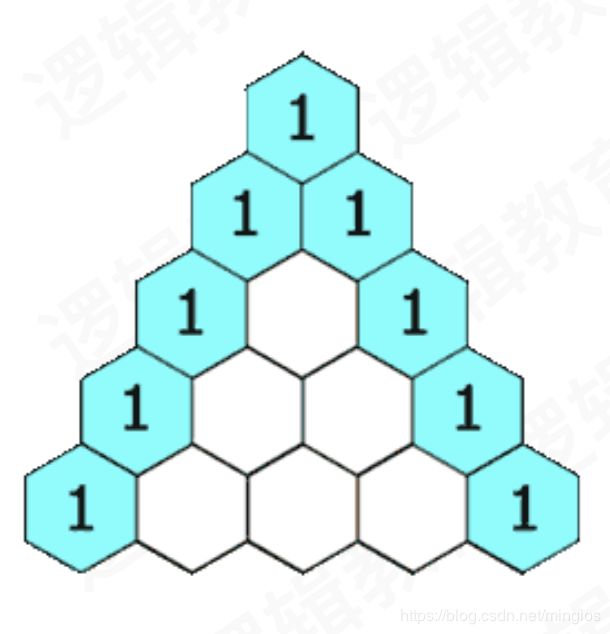
杨辉三角
思路:
1. 第一层循环控制行数i : 默认[i][0] = 1,[i][i] = 1
2. 第二层循环控制列数j : triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
实现:
int** generate(int numRows, int* returnSize){
*returnSize = numRows;
int **res = (int **)malloc(sizeof(int*)*numRows);
for (int i = 0; i < numRows; i++) {
res[i] = (int *)malloc(sizeof(int)*(i+1));
res[i][0] = 1;
res[i][i] = 1;
for (int j = 1; j < i; j++) {
res[i][j] = res[i-1][j] + res[i-1][j-1];
}
}
return res;
}
爬楼梯
假设你正在楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有 多少种不同的⽅法可以爬到楼顶呢?注意:给定 n 是⼀个正整数
示例1:
输入 :2,输出:2
有两种方法可以爬到楼顶 第1种:1阶+1阶(1+1) 第2种:2阶(2)
输入 :3,输出:3
有3种方法 1+1+1,1+2,2+1
实现方式1(递归求解法)
假设爬n个台阶有f(n)个可能:
1.假设先爬1阶,剩下n-1阶有f(n-1)种可能
2.假设先爬2阶,剩下n-2阶有f(n-2)种可能
因此爬n阶可以转化成2种爬n-1问题的和 f(n) = f(n-1) + f(n-2);
f(1)=1;
f(2)=1;
int ClimbStairs_1(int n){
if (n<1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return ClimbStairs_1(n-1) + ClimbStairs_1(n-2);
}实现方式2 (动态规划法)
动态规划(英语:Dynamic programming,简称 DP)是⼀种在数学、管理科学、计算机科学、经济学和⽣物信息 学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常适⽤用于有重叠⼦问题和最优⼦结构性质的问题,动态规划⽅法所耗时间往往少于朴素解法。
动态规划背后的基本思想非常简单。⼤致上,若要解⼀个给定问题,我们需要解其不同部分(即⼦问题),再根据⼦ 问题的解以得出原问题的解。动态规划往往用于优化递归问题,例如斐波那契数列,如果运⽤递归的⽅式来求解会重 复计算很多相同的⼦问题,利用动态规划的思想可以减少计算量量。
通常许多⼦问题⾮常相似,为此动态规划法试图仅解决每个⼦问题一次,具有天然剪枝的功能,从而减少计算量: ⼀旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同⼀个⼦问题解之时直接查表。这种做法在重 复⼦问题的数⽬关于输入的规模呈指数增⻓时特别有⽤。
int ClimbStairs(int n){
if(n==1) return 1;
int temp = n+1;
int *sum = (int *)malloc(sizeof(int) * (temp));
sum[0] = 0;
sum[1] = 1;
sum[2] = 2;
for (int i = 3; i <= n; i++) {
sum[i] = sum[i-1] + sum[i-2];
}
return sum[n];
}字符串串编码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注 意 k 保证为正整数。你可以认为输⼊入字符串总是有效的;输⼊字符串中没有额外的空格,且输⼊的⽅括号总是符合格式要求的。此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输⼊。
例如:
s = "3[a]2[bc]", 返回 "aaabcbc".
s = "3[a2[c]]", 返回 "accaccacc".
s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
思路:
例如:12[a]为例;
1.遍历字符串 S
2.如果当前字符不为方括号"]" 则入栈stack中;
2.如果当前字符遇到了方括号"]" 则:
① 首先找到要复制的字符,例如stack="12[a",那么我要首先获取字符a;将这个a保存在另外一个栈去tempStack;
② 接下来,要找到需要备份的数量,例如stack="12[a",因为出栈过字符"a",则当前的top指向了"[",也就是等于2;
③ 而12对于字符串是2个字符, 我们要通过遍历找到数字12的top上限/下限的位置索引, 此时上限curTop = 2, 下限通过出栈,top = -1;
④ 根据范围[-1,2],读取出12保存到strOfInt 字符串中来, 并且将字符"12\0",转化成数字12;
⑤ 当前top=-1,将tempStack中的字符a,复制12份入栈到stack中来;
⑥ 为当前的stack扩容, 在stack字符的末尾添加字符结束符合'\0';
实现:
char * decodeString(char * s){
/*.
1.获取字符串长度
2.设置默认栈长度50
3.开辟字符串栈(空间为50)
4.设置栈头指针top = -1;
*/
int len = (int)strlen(s);
int stackSize = 50;
char* stack = (char*)malloc(stackSize * sizeof(char));
int top = -1;
//遍历字符串,在没有遇到"]" 之前全部入栈
for (int i = 0; i < len; ++i) {
if (s[i] != ']') {
//优化:如果top到达了栈的上限,则为栈扩容;
if (top == stackSize - 1) {
stack = realloc(stack, (stackSize += 50) * sizeof(char));
}
//将字符入栈stack
stack[++top] = s[i];
printf("#① 没有遇到']'之前# top = %d\n",top);
}
else {
int tempSize = 10;
char* temp = (char*)malloc(tempSize * sizeof(char));
int topOfTemp = -1;
printf("#② 开始获取要复制的字符信息之前 # top = %d\n",top);
//从栈顶位置开始遍历stack,直到"["结束;
//把[a]这个字母a 赋值到temp栈中来;
//简单说,就是将stack中方括号里的字符出栈,复制到temp栈中来;
while (stack[top] != '[') {
//优化:如果topOfTemp到达了栈的上限,则为栈扩容;
if (topOfTemp == tempSize - 1) {
temp = realloc(temp, (tempSize += 10) * sizeof(char));
}
//temp栈的栈顶指针自增;
++topOfTemp;
//将stack栈顶字符复制到temp栈中来;
temp[topOfTemp] = stack[top];
//stack出栈,则top栈顶指针递减;
top--;
}
printf("#② 开始获取要复制的字符信息之后 # top = %d\n",top);
//找到倍数数字.strOfInt字符串;
//注意:如果是大于1位的情况就处理
char strOfInt[11];
//p记录当前的top;
int curTop = top;
printf("#③ 开始获取数字,数字位置上限 # curTop = %d\n",curTop);
//top--的目的是把"["剔除,才能找到数字;
top--;
//遍历stack得出数字
//例如39[a] 就要找到这个数字39.
//p指向当前的top,我就知道上限了; 那么接下来通过循环来找它的数字下限;
//结束条件:栈指针指向为空! stack[top] 不等于数字
while (top != -1 && stack[top] >= '0' && stack[top] <= '9') {
top--;
}
printf("#③ 开始获取数字,数字位置下限 # top = %d\n",top);
//从top-1遍历到p之间, 把stack[top-1,p]之间的数字复制到strOfInt中来;
//39中3和9都是字符. 我们要获取到这2个数字,存储到strOfInt数组
for (int j = top + 1; j < curTop; ++j) {
strOfInt[j - (top + 1)] = stack[j];
}
//为字符串strOfInt数组加一个字符结束后缀'\0'
strOfInt[curTop - (top + 1)] = '\0';
//把strOfInt字符串转换成整数 atoi函数;
//把字母复制strOfInt份到stack中去;
//例如39[a],就需要把复制39份a进去;
int curNum = atoi(strOfInt);
for (int k = 0; k < curNum ; ++k) {
//从-1到topOfTemp 范围内,复制curNum份到stackTop中去;
int kk = topOfTemp;
while (kk != -1) {
//优化:如果stack到达了栈的上限,则为栈扩容;
if (top == stackSize - 1) {
stack = realloc(stack, (stackSize += 50) * sizeof(char));
}
//将temp栈的字符复制到stack中;
//stack[++top] = temp[kk--];
++top;
stack[top] = temp[kk];
kk--;
}
}
free(temp);
temp = NULL;
}
}
//realloc 动态内存调整;
//void *realloc(void *mem_address, unsigned int newsize);
//构成字符串stack后, 在stack的空间扩容.
char* ans = realloc(stack, (top + 1) * sizeof(char));
ans[++top] = '\0';
//stack 栈不用,则释放;
free(stack);
return ans;
}去除重复字母
给你一个仅包含小写字母的字符串,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证返回结果的字典序最小(要求不能打乱其他字符的相对位置)
示例1:
输入:"bcabc"
输出:"abc"
示例2:
输入:"cbacdcbc"
输出:"acdb"
解题关键:
字典序: 字符串之间比较和数字比较不一样; 字符串比较是从头往后挨个字符比较,那个字符串大取决于两个字符串中第一个对应不相等的字符; 例如 任意一个a开头的字符串都大于任意一个b开头的字符串;例如字典中apple 大于 book;
题目的意思,你去除重复字母后,需要按最小的字典序返回.并且不能打乱其他字母的相对位置;
例如 bcabc 你应该返回abc, 而不是bca,cab;
例如 cbacdcbc 应该返回acdb,而不是cbad,bacd,adcb
例如 zab,应该返回zab,而不是abz;
思路:
1. 判断字符串可能出现的特殊情况
2. 用一个record数组记录字符串中字母出现的次数;
3. 申请一个字符串栈stack用来存储去除重复字母的结果,并利用它的特性帮助我们找到正确的次序;
4. 遍历字符串s
5. 从0~top,遍历stack 判断当前字符s[i]是否存在于栈stack中
如果当前字符是否存在于栈的定义一个falg 标记isExist, 0表示不存在, 1表示存在
6.如果isExist存在,record[s[i]]位置上的出现次数减一,并继续遍历下一个字符; 表示当前的stack已经有这个字符了没有必要处理这个重复的字母;
7.如果isExist不存在,则
如果不存在,则需要循环一个找到一个正确的位置,然后在存储起来;
如果不存在,跳过栈中所有比当前字符大、且后面还会出现的元素,然后将当前字符入栈
top > -1表示栈非空
stack[top] > s[i]表示栈顶元素比当前元素大
record[stack[top]] > 1表示后面还会出现
通过一个while循环找到将栈中位置错误的数据,出栈. 找当前合适的位置,则结束while循环;
找到合理的位置后,则将当前字符s[i]入栈;
8.直到遍历完所有字符后,则为字符串栈stack 添加一个结束符'\0',并返回当前字符串首地址;
实现:
char *removeDuplicateLetters(char *s)
{
/*
① 特殊情况处理,s为空,或者字符串长度为0;
② 特殊情况,s的长度为1,则没有必要后续的处理,则直接返回s;
*/
if (s == NULL || strlen(s) == 0) {
return "";
}
if (strlen(s) == 1) {
return s;
}
//record数组,用来记录字符串s中每个字符未来会出现的次数;
char record[26] = {0};
int len = (int)strlen(s);
//申请一个字符串stack;(用栈的特性来进行stack字符串的数据进出)
char* stack = (char*)malloc(len * 2 * sizeof(char));
//memset(void *s, int ch, size_t n) 将stack len*2*sizeof(char)长度范围的空间填充0;
memset(stack, 0, len * 2 * sizeof(char));
//stack 栈顶赋初值为-1;
int top = -1;
//1.统计每个字符的频次
//例如bcabc recod[26] = {1,2,2};
int i;
for (i = 0; i < len; i++) {
record[s[i] - 'a']++;
}
//2.遍历s,入栈
for (i = 0; i < len; i++) {
//isExist 标记, 判断当前字符是否存在栈中;
int isExist = 0;
//①从0~top,遍历stack 判断当前字符s[i]是否存在于栈stack中
//如果当前字符是否存在于栈的flag, 0表示不存在, 1表示存在
//top指向栈顶(也是执行stack字符串最后一个字符的位置,表示字符串长度上限)
for (int j = 0; j <= top; j++) {
if (s[i] == stack[j]) {
isExist = 1;
break;
}
}
//② 如果存在,record[s[i]]位置上的出现次数减一,并继续遍历下一个字符
//③ 如果不存在,则需要循环一个正确位置存储起来;
//④ 如果不存在,跳过栈中所有比当前字符大、且后面还会出现的元素,然后将当前字符入栈
// top > -1表示栈非空
//stack[top] > s[i]表示栈顶元素比当前元素大
//record[stack[top]] > 1表示后面还会出现
//例如b,c因为不符合以下条件会直接入栈.stack[] = "bc",但是当当前字符是"a"时,由于bcabc,a不应该是在stack的顺序是"bca",所以要把位置不符合的字符出栈;
//top = 1,stack[top] > s[i], c>a; 并且stack[top] 在之后还会重复的出现,所以我们可以安心的把stack中的栈顶C出栈,所以stack[]="b",top减一后等于0; 同时也需要将record[c]出现次数减一;
//top=0,stack[top]>s[i],b>a,并且stack[top] 在之后还会出现,所以stack把栈顶b出栈,所以此时栈stack[]="",top减一后等于-1, 此时栈中位置不正确的字符都已经移除;
if (isExist == 1) {
record[s[i] - 'a']--;
} else {
while (top > -1 && stack[top] > s[i] && record[stack[top] - 'a'] > 1) {
// 跳过该元素,频次要减一
record[stack[top] - 'a']--;
// 出栈
top--;
}
//⑤ 结束while 循环;
//循环结束的3种可能性:(1)移动到栈底(top == -1) ; (2)栈顶元素小于当前元素(stack[top] <= s[i]) (3)栈顶元素后面不出现(record[stack[top]] == 1)
// 此时,当前元素要插入到top的下一个位置
// top往上移动1位
top++;
// 入栈
stack[top] = s[i];
}
}
//结束栈顶添加字符结束符
stack[++top] = '\0';
return stack;
}