【多视图几何】对极几何与基本矩阵

本文未指明图片来源为 Multiple View Geometry in Computer Vision 。

读 Multiple View Geometry in Computer Vision 所做笔记。

第 9 章 《对极几何与基本矩阵》，Epipolar Geometry and the Fundamental Matrix。

对极几何研究的对象是双视图几何，即两张相邻影像的位姿关系。

1. 对极几何基本概念

1. 核点（epipole）：基线（baseline）与成像平面的交点。同时极点也可以理解为相邻影像成像中心在本影像上的像，因为基线是两个相邻影像成像中心的连线。
2. 核平面（epipolar plane）：含有基线的平面，是一簇平面。可以看做是由基线与空间中任意一点构成的平面。
3. 核线（epipolar line）：核平面与成像平面的交线。可以看做是成像平面上的任意一点（非核点）与核点所定义的直线。

2. 基本矩阵 F

基本矩阵可以看做是将点投影（转换）为直线，将左影像上的一个点投影到右影像上形成一条核线。

2.1 几何推导基本矩阵

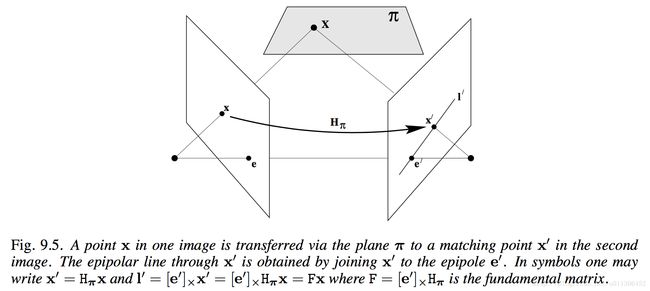
假设有一空间平面 π ，将 π 上的点 X 投影到左右影像上，可以得到这个三维点在两张影像上的像 x,x′ ，将空间平面上所有的点都进行投影，能够得到左右影像上所有点的对应关系，这种对应关系可以使用单应矩阵（homography matrix, page 87） Hπ 描述：

x′=Hπx

右影像上的核线 l′ 可以由两个点——右影像上的核点 e′ 与右影像上的任意一点 x′ ——确定：

l′=e′×x′=[e′]×x′

将 x′=Hπx 代入：

l′=[e′]×Hπx=Fx

这样就得到了基本矩阵的定义：

F=[e′]×Hπ

因为 x′ 在右核线 l′ 上，所以点积为 0 ：

x′Tl′=x′TFx=0

2.2 代数推导基本矩阵

空间中三维点 X 反向投影到左影像上得到点 x ，这个过程可以用投影矩阵 PX=x 进行描述。

现在想办法将 X 用 x 表示， P 是一个 4x3 的矩阵，不可逆。使用 P 的伪逆： P+=PT(PPT)−1 ，得

X=P+x

对于左影像 X 是对应一条直线上的所有点，可以使用下面的方程表示这一条直线：

X(λ)=P+x+λC

现在将这一条直线投影到右影像上，即可得到右影像的核线。投影的方式是在 X(λ) 上找到两个点，将这两点分别投影到右影像上，投影后的两个点确定右影像上的核线。

取 λ 为0，得到直线上的第一个点 P+x ，取 λ 为 ∞ 得到直线上的第二个点 C （即左影像的成像中心）。将这个两个点分别投影到右影像上，得到 P′P+x 与 P′C 。 P′C=e′ ，左影像成像中心在右影像上的成像是核点。这两个点叉乘即可得到右影像上的核线：

l′=(P′C)×(P′P+x)=[e′]×P′P+x=Fx

所以 F=[e′]×P′P+ 。

2.3 基础矩阵的性质

1. 转置对称性：如果 F 是一对影像 (P,P′) 的基础矩阵（即 x′Fx=0 ），反过来 (P′,P) 的基础矩阵是 FT 。证明很简单，直接对 x′Fx=0 两侧分别转置，得到 xTFTx′=0 。
2. 核线：对于左影像上任意一点 x ，其在右影像上的核线为 l′=Fx 。
3. 核点：任何核线都会经过核点，所以有对于左影像上任意一点 x ， e′Tl′=e′T(Fx)=0 ，于是有 e′TF=0 。同理有 Fe=0 。
4. F 具有7自由度：一个 3x3 的单应矩阵，具有8个自由度，而 F 还满足 detF=0 ，所以 F 具有7个自由度。
5. F 是相关的： F 将左影像上的一点 x 投影到右影像上一条核线 l′ ，投影本质上是将 x 与左核点的连线 l 投影到右影像上的核线 l′ ，所以右影像上的一条核线 l′ 对应的是左影像上的一条核线 l ，这种点到线的投影不可逆。

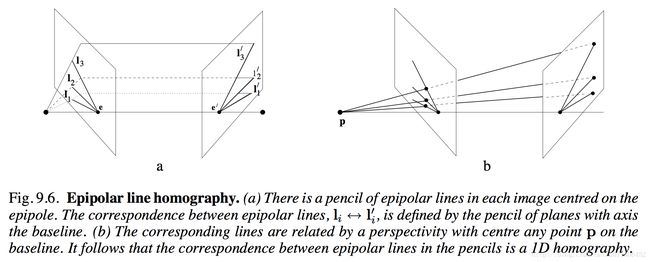
2.4 核线的单应性

一张截图说明一切：

两张影像上核线的对应关系可以看作是中心投影，投影中心 p 位于核线上。

求左核线 l 对应的右核线 l′ 是现在左核线上找一点 x 使用基本矩阵通过 l′=Fx 计算得到。 x 是任意的，只需要其在 l 上就行。可以通过做核线 l 与另一条不经过核点直线的交点计算得到 x 。假设另外一条直线为 k ，那么 l 与 k 的交点为 [k]×l ，所以右核线的计算方法如下：

l′=F[k]×l

直线 k 选择为 e 能够简化计算，直线 e 肯定不会通过核点 e （ eTe≠0 ），所以对应核线的计算公式整理如下：

l′=F[e]×l

l=FT[e′]×l′

3. 从特殊运动中推导基础矩阵

3.1 仅有位移

在仅有位移的情况下，左右相机的内参也一致，左右相机的投影矩阵可以写成 P=K[I|0],P′=K[I|t] ， 由

F=[e′]×K′RK−1

可以得到

F=[e′]×

计算两张影像上影像坐标的对应关系。

x=PX=K[I|0]X 左影像的投影关系，现在反求空间点 X 的坐标， (X,Y,Z)T=ZK−1x ，其中 Z 是标量，表示 X 的深度。将 X 的坐标计算结果带入右影像的投影关系 x′=P′X=K[I|t]X ，可以得到 x′ 与 x 的关系：

x′=x+Kt/Z

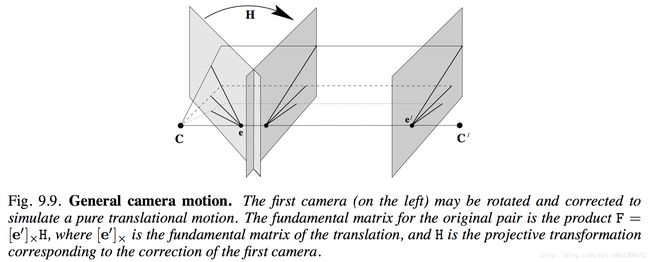
3.2 旋转与位移

当两张影像相对位姿含有旋转与位移时，先将左影像进行旋转，与右影像对齐（具有相同的姿态）。于是将问题简化为上述的位移问题。

将一张影像仅做旋转，相当于将影像进行一次平行投影（投影点在无穷远处），如下图：

这个平行投影可以使用单应矩阵 H∞ 表示， H∞ 通过两张影像的投影矩阵计算得到。

x=K′[I|0]X

x′=K[R|0]X=KRK−1K[I|0]X=KRK−1x

将上式的 x′ 替换 x′=x+Kt/Z 中的 x ，即可得到最后的结果：

x′=KRK−1x+Kt/Z