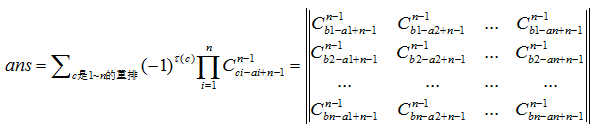牛客网暑期ACM多校训练营（第一场）- （A，D，J）

 

A	Monotonic Matrix

题意：求满足下列条件的n*m的矩阵有多少种，①.元素属于{0,1,2}；②.每行的值都递增；③.每列的值都递增。

解析：如果矩阵行、列号往下往右递增，发现0左上，2在右下，考虑0和1的分界线，1和2的分界线，是 (n, 0) 到 (0,m) 的两条不相交（可重合）路径，由于从（n,0）出发只有右或上两个选择所以下一步一定在(n-1,0)或(n,1)，同理(0,m)的上一步一定是（0，m-1）或（1，m），不想交的情况出现在一条从(n-1,0)出发到达(0,m-1)，一条从(1,n)出发到达(1,m)时，此时总方案数为：（Cn+m, n）*（Cn+m, n）

         而此时是可能有相交的，而相交情况等价于一条从(n-1,0)出发到(1,m)，一条从(1,n)出发到达(0,m-1)的情况，也就是要减去方案数（Cn+m, m - 1）*（Cn+m, n-1）

注：组合数学中，对于矩阵中从(x1,y1)到（x2,y2）的方案数为Cx2-x1,y2-y1。（假设x2>x1,y2>y1）

        题目可推广到定理 Lindström–Gessel–Viennot lemma，定理解决的问题是：通常都是上面有点集A，下面有点集B，然后求每个A到对应B的不相交路径总数，公式计算方式如下

 其中e（a， b）表示a 到 b的路径条数，具体到组合数学公式如下

 证明大体如下:

         首先考虑两个棋子的情况，即一个棋子从a1到b1，另一个棋子从a2到b2，两条路径不交叉的方案数，首先不考虑交叉方案数显然是C(b1-a1+n-1,n-1)*C(b2-a2+n-1,n-1)，对于一个a1->b1,a2->b2且路径交叉的方案，如果我们把最下面一个交叉点之后的两条路径交换那么就对应了一个a1->b2,a2->b1的方案；对于一个a1->b2,a2->b1的方案，显然这两条路径必然会相交，那么我们把最后一个交叉点之后的两条路径交换就又对应一个a1->b1,a2->b2的路径交叉的方案，故我们建立了a1->b1,a2->b2交叉路径与a1->b2,a2->b1的方案的一一对应，那么不合法方案数就是C(b2-a1+n-1,n-1)*C(b1-a2+n-1,n-1) 
对于多个棋子的情况，由容斥原理，假设某些棋子路径发生了交叉，那么我们采用两个棋子的分析方法，把这些交叉的路径从最后下面一个交叉点之后交换，那么就变成了一个1~n序列的重排，我们不妨设其为c序列，表示第i个棋子从(1,ai)出发到(n,ci)，那么这个排列对答案的贡献就取决于c序列的逆序对数，逆序对数为奇则做负贡献，为偶则做正贡献，那么就有上图。【此处来自第一个链接】

参考：https://blog.csdn.net/V5ZSQ/article/details/52419187

           https://www.xuebuyuan.com/1939897.html

           https://www.cnblogs.com/joyouth/p/5607781.html 

代码：

#include
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const ll maxN=1e3+5;

int n,m;
ll C[maxN*2][maxN*2];//存组合数
void init_c()   //计算组合数
{
    for(int i=0;i<2002;i++)
    {
        for(int j=0;j<=i;j++)
        {
            if(j==0||i==j) C[i][j]=1;
            else C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
        }
    }
}
int main()
{
    init_c();
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        ll ans=((C[n+m][n]*C[n+m][n])%mod - (C[n+m][m-1]*C[n+m][n-1])%mod + mod)%mod;
        printf("%lld\n",ans);
    }
}

 

 

D	Two Graphs

题意：求把G2删掉某些边后和G1同构的不同的方案的数量。

解析：看到n只到8，那么可以用next_permutation枚举点集V的8！种重构情况，然后将根据每次重构情况将对应G1中的边集E1中的端点对应变换，看得到的新边是否在E2中，如果是那就是一种同构方案。注意用map判重。

我的代码wa了，先贴上别人的代码：https://www.nowcoder.com/acm/contest/view-submission?submissionId=29576073

#include 
using namespace std;
 
typedef long long ll;
 
const int N = 10;
const int M = N * N;
int n, m1, m2;
int g1[N][N], g2[N][N];
int pi[N];
set ans;
 
int main() {
    while (~scanf("%d%d%d", &n, &m1, &m2)) {
        memset(g1, 0, sizeof g1);
        memset(g2, 0, sizeof g2);
        memset(pi, 0, sizeof pi);
        ans.clear();
        for (int i = 0; i < m1; ++i) {
            int u, v;  scanf("%d%d", &u, &v);
            u--; v--;
            g1[u][v] = g1[v][u] = 1;
        }
        for (int i = 0; i < m2; ++i) {
            int u, v;  scanf("%d%d", &u, &v);
            u--; v--;
            g2[u][v] = g2[v][u] = 1;
        }
        iota(pi, pi + n, 0);
        do {
            bool ok = true;
            for (int i = 0; i < n && ok; ++i)
                for (int j = 0; j < i; ++j)
                    if (g1[pi[i]][pi[j]] && !g2[i][j]) {
                        ok = false;
                        break;
                    }
            if (ok) {
                int counter = 0;
                int state = 0;
                for (int i = 0; i < n; ++i)
                    for (int j = 0; j < i; ++j) {
                        if (!g1[pi[i]][pi[j]] && g2[i][j])
                            state |= (1 << counter);
                        counter++;
                    }
                // cout << state << endl;
                ans.insert(state);
            }
        } while (next_permutation(pi, pi + n));
        cout << ans.size() << endl;
    }
}

 

 

J	Different Integers

题意：给出长为n的数组a1,a2...an，有q次查询，每次查询给出Li,Ri，让求数组中去掉开区间(aLi,aRi)后剩余部分中不同元素的个数。

解析：有线段树的典型例题是求区间中不同数的个数，现在每次查询是求区间[a1,an]减去开区间(aLi,aRi)后剩余的[a1,aLi-1]和[aRi+1,an]两个区间中不同元素的个数，我们只需将原数组[a1,a2...an]扩展为[a1,a2...an,a1,a2...an]两个区间中的统计又变为了一个区间中的统计，就可以用之前的模板了。

代码：

#include
using namespace std;
typedef long long ll;
const ll maxN=1e5+5;

int n,q;
int a[maxN<<1],tree[maxN<<1];
int ans[maxN<<1],vis[maxN<<1];

struct Node{
    int x,y,index;
    bool operator < (const Node & obj) const
    {
        return y0)
    {
        res+=tree[x];
        x-=lowbit(x);
    }
    return res;
}

int main()
{
    int x,y;
    while(scanf("%d%d",&n,&q)!=EOF)
    {
        memset(vis,0,sizeof(vis));
        memset(ans,0,sizeof(ans));
        memset(tree,0,sizeof(tree));

        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            a[i+n]=a[i];
        }
        for(int i=1;i<=q;i++)
        {
            scanf("%d%d",&x,&y);
            node[i].x=y;
            node[i].y=x+n;
            node[i].index=i;
        }
        sort(node+1,node+1+q);

        int it=1;//当前处理的区间
        for(int i=1;i<=2*n&&it<=q;i++)
        {
            if(vis[a[i]])
                add(vis[a[i]],-1);
            vis[a[i]]=i;
            add(vis[a[i]],1);

            while(it<=q&&i>=node[it].y)
            {
                ans[node[it].index]=sum(node[it].y)-sum(node[it].x-1);
                it++;
            }
        }

        for(int i=1;i<=q;i++)
            printf("%d\n",ans[i]);
    }
    return 0;
}

 还有一种思路是：（来自https://www.cnblogs.com/rikka/p/9341355.html）

考虑一个元素有两个属性：第一次出现的地方和最后一次出现的地方：记为first[x]和last[x]

则答案应为，总元素个数 - 只在给定区间内出现的元素个数。

则问题实际上转化为 求count（first[x],last[x] ∈ (l,r)）。

考虑实际上对于每个元素来说，first[x],和last[x]可以理解为二元组——或者二维空间的坐标，则问题实际转化为二维空间内的点统计问题。因为元素太多，所以考虑使用主席树的方式来构造二维线段树。

但是进一步观察可得，每一行每一列都只有一个元素可能存在。于是如果保证二元组（first[x],last[x]）中last[x]保持递增顺序其实就没必要一定要构造主席树来进行数字统计——直接用树状数组挂vector之后用lower_bound查出现位置即可。