# cs231n （二）线性分类器

cs231n （二）线性分类器

标签（空格分隔）： 神经网络

---

0.回顾

cs231n （一）图像分类识别讲了KNN

k-Nearest Neighbor分类器存在以下不足：

• 分类器必须记住所有训练数据并将其存储起来，以便于未来测试数据用于比较,存储空间上是低效的.

• 对一个测试图像进行分类需要和所有训练图像作比较，算法计算资源耗费高。

1.线性分类

卷积神经网络:
主要有两部分组成,

• 一个是评分函数（score function），它是原始图像数据到类别分值的映射,就是原数据啦!
• 另一个是损失函数（loss function），用来量化预测分类标签的得分与真实标签之间一致性的。该方法可转化为一个最优化问题.

从图像到标签分值的参数化映射

就是定义一个评分函数: 就是把图像量化,给电脑看.

线性分类器: 从最简单的概率函数开始，一个线性映射
$$f(x_i,W,b)=W{x}_i+b$$
如果是CIFAR-10: $x_i:$ 3072x1, $W$: 10x3072, $b$: 10x1

• $W x_i $就可以有效地评估10个分类器，其中每个分类器是W的一行
• 训练数据是用来学习到参数W和b的，一旦完成，就可以丢弃，留下学习到的参数.
• 只需要做一个矩阵乘法和一个矩阵加法就能对一个测试数据分类，这比k-NN中将测试图像和所有训练数据做比较的方法快.

---

理解线性分类器

线性分类器: 图像中3个颜色通道中所有像素的值与权重的矩阵乘，从而得到分类分值。

根据我们对权重设置的值，对于图像中的某些位置的某些颜色，函数表现出喜好或者厌恶.

举个例子，想象“船”:就是被大量的蓝色所包围（对应的就是水）。

那么“船”分类器在蓝色通道上的权重就有很多的正权重，而在绿色和红色通道上的权重为负的就比较多.

---

假设图像只有4个像素（都是黑白像素，这里不考虑RGB通道），有3个分类（红色代表猫，绿色代表狗，蓝色代表船，注意，这里的红、绿和蓝3种颜色仅代表分类，和RGB通道没有关系）。

首先将图像像素拉伸为一个列向量，与W进行矩阵乘，然后得到各个分类的分值。

需要注意的是，这个W一点也不好：猫分类的分值非常低。从上图来看，算法倒是觉得这个图像是一只狗

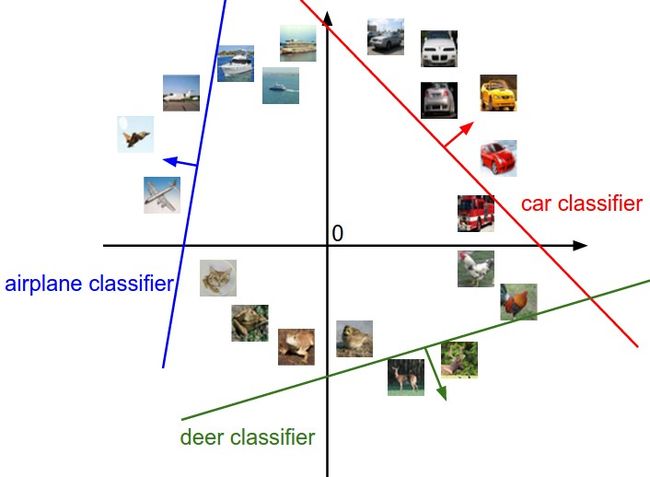
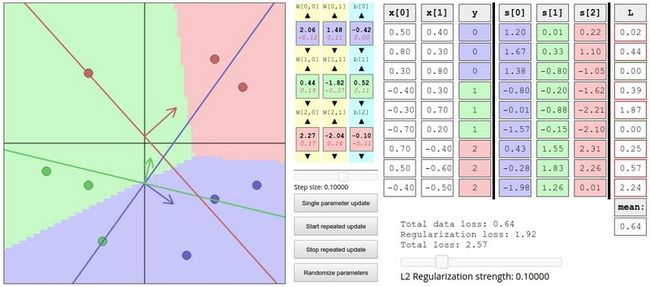
将图像看作是高纬度的点: 每张图像是3072维空间中一个点,整个数据集就是一个点的集合，每个点都带有1个分类标签.(看图)

假设把这些维度挤压到二维，那么就可以看看这些分类器在做了啥：

从上面可以看到，W的每一行都是一个分类类别的分类器。
对于这些数字的几何解释是：如果改变其中一行的数字，会看见分类器在空间中对应的直线开始向着不同方向旋转。

而偏差b，则允许分类器对应的直线平移, 如果没有偏差，无论权重如何，在x_i=0时分类分值始终为0。这样所有分类器的线都必须穿过原点。

将线性分类器看做模板匹配: 我们没有使用所有的训练集的图像来比较，而是每个类别只用了一张图片（这张图片是我们学习到的，而不是训练集中的某一张），我们会使用内积来计算向量间的距离，而不是使用L1或者L2距离。

这里展示的是以CIFAR-10为训练集，学习后的权重的例子。

船的模板确实有很多蓝像素, 如果图像是一艘船行驶在大海上，那么这个模板利用内积计算图像将给出很高的分数.

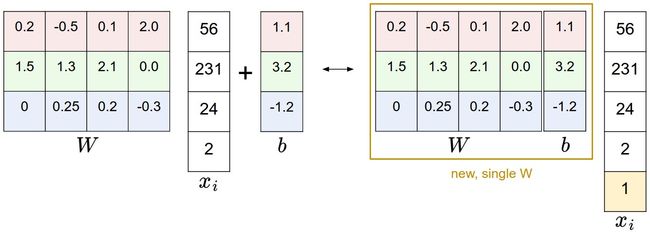
偏差和权重的合并技巧:

以CIFAR-10为例，那么$x_i$的大小就变成[3073x1]，不是[3072x1]了，多出了包含常量1的1个维度）
W大小就是[10x3073]了, W中多出来的这一列对应的就是偏差值b，看图!

1. 左边是先做矩阵乘法然后做加法
2. 右边是将输入向量的维度增加1个1的维度，在权重矩阵中增加一个偏差列b，最后做一个矩阵乘法.
   这样只需要学习一个权重矩阵,不用学W和b了.

---

图像数据预处理: 之前是0-255,现在对于输入的特征做归一化,对每个特征减去平均值来中心化数据很重要,即让数值分布区间变为[-1, 1]。零均值的中心化是很重要的,我们先了解梯度下降.

损失函数

评分函数搞定了,看看损失函数,其实就是看实际分数和已知分数的差越小越好, 聪明,就是零最好!

2.支持向量机(SVM)

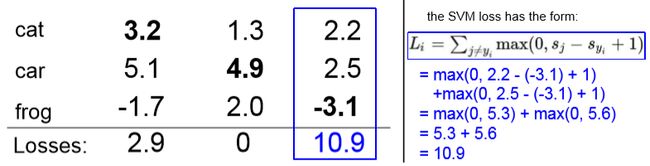
先看看SVM的损失函数: 那么第i个数据损失的定义就是

$$\to L_i=\sum _{j̸=y_i}max(0,s_j-s_{y_i}+\Delta )$$

---

具体如何计算,这个说的很清楚啦!

对于线性模型,评分函数是 $f(x_i,W)=W_{x_i}$, 那么损失函数就是:
$$L_i=\sum _{j̸=y_i}max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta )$$

关于零阈值: max(0, -)函数, 也叫折叶损失, 那么平方折叶损失SVM, 就是: (L2 -SVM), 也就是$max(0,-{)}_2$

**正则化（Regularization)?*不知道你看出来上面损失函数的问题了吗,反正我是没有(haha.gif)

我们需要惩罚一下这个权重W, 方法: 正则化惩罚, $R(W)={\sum }_k{\sum }_l{W}_{k,l}^2$

那么我们有:
$$L=\frac{1}{N}\sum _{j̸=y_i}max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta )+\lambda \sum _k\sum _l{W}_{k,l}^2$$

N是训练集的数据量,最好对大数值权重进行惩罚，能提升其泛化能力，因为剔除能独自对整体score有太大的影响的维度.

Code:无正则化部分的损失函数的Python实现，非向量化和半向量化两种

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in xrange(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment

实际考量

超参数 $\Delta$ 的选取:
该超参数在绝大多数情况下设为$\Delta =1.0$都是安全的。超参数$\Delta$和$\lambda$看起来是两个不同的超参数，

实际上他们一起控制同一个权衡：即损失函数中的数据损失和正则化损失之间的权衡

梯度计算 在训练过程中，我们需要通过最优化方法来是代价函数的损失值达到尽可能的小，所以我们对代价函数进行微分，然后计算其偏导数，得到以下公式
$${\Delta }_{w_i}{L}_i=1(w_j^T{x}_i-w_{y_i}^T{x}_i+\Delta >0)x_i$$
对于每一个训练样本，我们计算它在每个分类上的得分，每当它在某一分类产生了损失（即scores[y[!i] - scores[y[i]] + delta > 0），那么我们就将该分类上的参数梯度+Xi

3.Softmax分类器

它也很常见,它的损失函数肯定和SVM不一样啊! 亲爱的小傻瓜.

和SVM不同，Softmax的输出啊（归一化的分类概率）更加直观，并且从概率上可以证明.

在Softmax分类器中，函数映射$f(x_i;W)=W{x}_i$保持不变,并且将折叶损失（hinge loss）替换为交叉熵损失（cross-entropy loss）.

$$Li=-log(\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}})$$ 或等价的$$L_i=-f_{y_i}+log(\sum _j{e}^{f_j})$$

在上式中，使用$f_j$来表示分类评分向量f中的第j个元素, 其中函数$f_j(z)=\frac{e^{z_j}}{{\sum }_k{e}^{z_k}}$被称作softmax 函数.

重mei点yong:

信息理论视角：在“真实”分布p和估计分布q之间的交叉熵定义如下

$$H(p,q)=-\sum _{x}p(x)logq(x)$$
因此，Softmax分类器所做的就是最小化在估计分类概率$$\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}$$ 和“真实”分布之间的交叉熵.

概率论解释：

$$P(y_i|x_i,W)=\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}$$

可以解释为是给定图像数据$x_i$，以$W$为参数，分配给正确分类标签$y_i$的归一化概率.

我们在最小化正确分类的负对数概率，这可以看做是在进行最大似然估计（MLE）,损失函数中的正则化部分R(W)可以看做是权重矩阵W的高斯先验，这里进行的是最大后验估计（MAP）而不是最大似然估计.

实际情况：数值稳定。编程实现softmax函数计算的时候，中间项$e^{f_{y_i}}$和${\sum }_j{e}^{f_j}$因为存在指数函数，所以数值可能超级大。

除以大数值可能导致数值计算的不稳定，所以学会使用归一化技巧很重要!
在分式的分子和分母都乘以一个常数C看看，并把它变换到求和之中，就能得到一个从数学上等价的公式：

$$\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}=\frac{C{e}^{f_{y_i}}}{C{\sum }_j{e}^{f_j}}=\frac{e^{f_{y_i}+logC}}{{\sum }_j{e}^{f_j+logC}}$$

什么? C是多少?

高数告诉我们, 在这里C的值可自由选择，不会影响计算结果.
实现代码

f = np.array([123, 456, 789]) # 例子中有3个分类，数值都很大
p = np.exp(f) / np.sum(np.exp(f)) # 数值问题，可能导致数值爆炸a

# 那么将f中的值平移到最大值为0：kankan 

f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) 

让人迷惑的命名规则：SVM分类器使用的是折叶损失（hinge loss），有时候又被称为最大边界损失（max-margin loss）, Softmax分类器使用的是交叉熵损失（corss-entropy loss）。

Softmax分类器的命名是从softmax函数那里得来的，softmax函数将原始分类评分变成正的归一化数值，所有数值和为1，这样处理后交叉熵损失才能应用

4.SVM和Softmax的比较

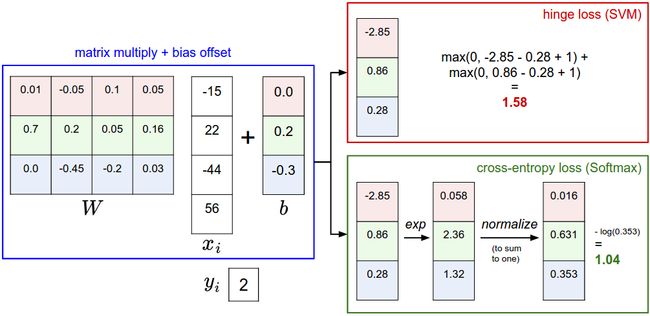
重点,拿出你的红笔来,soga! 看图,看我干嘛,我脸上有花啊!!!

记住一点,高考必考, Softmax分类器将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。

SVM的损失值是1.58
Softmax的损失值是0.452

但要注意这两个数值没有可比性。只在给定同样数据，在同样的分类器的损失值计算中，它们才有意义。

Softmax为每个分类提供了“可能性:

SVM分类器可能给你的是一个[12.5, 0.6, -23.0]对应分类“猫”，“狗”，“船
softmax分类器可以计算出这三个标签的”可能性“是[0.9, 0.09, 0.01]

举个例子，假设3个分类的原始分数是[1, -2, 0]，那么softmax函数就会计算
$$[1,-2,0]\to [e^1,e^{-2},e^0]=[2.71,0.14,1]\to [0.7,0.04,0.26]$$

现在，假设正则化参数λ更大，那么权重W就会被惩罚的更大,假设小了一半吧[0.5, -1, 0]那么softmax函数的计算就是：

$$[0.5,-1,0]\to [e^{0.5},e^{-1},e^0]=[1.65,0.73,1]\to [0.55,0.12,0.33]$$

结果就是:概率的分布更加分散!

特点:

• softmax分类器对于分数是永远不会满意的,这是马爸爸还有我(haha.gif)
• SVM只要边界值被满足了就满意了，这是国企,大锅饭.
  

5.总结

• 定义了从图像像素映射到不同类别的分类评分的评分函数,今天学的评分函数是一个基于权重W和偏差b的线性函数
• 与kNN分类器不同，参数方法的优势在于一旦通过训练学习到了参数，就可以将训练数据丢弃了
• 介绍了偏差tricks，让我们能够将偏差向量和权重矩阵合二为一,就是偷懒呗,效率呗!
• 损失函数定义,SVM和Softmax线性分类器最常用的2个损失函数.

6. 下季预告

这不是损失函数搞定了,现在要想办法把它最小化,专业一点:最优化下节课有你好受的!!!

转载和疑问声明

如果你有什么疑问或者想要转载，没有允许是不能转载的哈
赞赏一下能不能转？哈哈，联系我啊，我告诉你呢 ~~
欢迎联系我哈，我会给大家慢慢解答啦~~~怎么联系我？ 笨啊~ ~~ 你留言也行

你关注微信公众号1.机器学习算法工程师：2.或者扫那个二维码，后台发送 “我要找朕”，联系我也行啦！

（爱心.gif） 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊，如果你觉得本文有帮助，三毛也是爱！

我祝各位帅哥，和美女，你们永远十八岁，嗨嘿嘿~~~