Codeforces Round #645 (Div. 2)题目+详解+代码（A、B、C、D）

A. Park Lighting

来源：http://codeforces.com/contest/1358/problem/A

Due to the coronavirus pandemic, city authorities obligated citizens to keep a social distance. The mayor of the city Semyon wants to light up Gluharniki park so that people could see each other even at night to keep the social distance.

The park is a rectangular table with n rows and m columns, where the cells of the table are squares, and the boundaries between the cells are streets. External borders are also streets. Every street has length 1. For example, park with n=m=2 has 12 streets.

You were assigned to develop a plan for lighting the park. You can put lanterns in the middle of the streets. The lamp lights two squares near it (or only one square if it stands on the border of the park).

The park sizes are: n=4, m=5. The lighted squares are marked yellow. Please note that all streets have length 1. Lanterns are placed in the middle of the streets. In the picture not all the squares are lit.
Semyon wants to spend the least possible amount of money on lighting but also wants people throughout the park to keep a social distance. So he asks you to find the minimum number of lanterns that are required to light all the squares.

Input
The first line contains a single integer t (1≤t≤104) — the number of test cases in the input. Then t test cases follow.

Each test case is a line containing two integers n, m (1≤n,m≤104) — park sizes.

Output
Print t answers to the test cases. Each answer must be a single integer — the minimum number of lanterns that are required to light all the squares.

Example
inputCopy
5
1 1
1 3
2 2
3 3
5 3
outputCopy
1
2
2
5
8
Note
Possible optimal arrangement of the lanterns for the 2-nd test case of input data example:

Possible optimal arrangement of the lanterns for the 3-rd test case of input data example:

题意：
给你一个 n*m 的表格，单元格的边界是街道，长度都为1；现在街道中央放路灯·，其能照亮街道两旁的两个方块。问最少需要多少个灯才能照亮整个公园

思路:
比较好想，算出所有表格的数量，既然是一盏灯两个方块，那就除以2，如果余1，那就ans再加上1，具体看代码吧

代码实现：

#include
using namespace std;
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		int n, m;
		cin >> n >> m;
		int ans = n * m / 2;
		if ((n * m) % 2 != 0)ans += 1;
		cout << ans << endl;
	}
	return 0;
}

B. Maria Breaks the Self-isolation

来源：http://codeforces.com/contest/1358/problem/B

Maria is the most active old lady in her house. She was tired of sitting at home. She decided to organize a ceremony against the coronavirus.

She has n friends who are also grannies (Maria is not included in this number). The i-th granny is ready to attend the ceremony, provided that at the time of her appearance in the courtyard there will be at least ai other grannies there. Note that grannies can come into the courtyard at the same time. Formally, the granny i agrees to come if the number of other grannies who came earlier or at the same time with her is greater than or equal to ai.

Grannies gather in the courtyard like that.

Initially, only Maria is in the courtyard (that is, the initial number of grannies in the courtyard is 1). All the remaining n grannies are still sitting at home.
On each step Maria selects a subset of grannies, none of whom have yet to enter the courtyard. She promises each of them that at the time of her appearance there will be at least ai other grannies (including Maria) in the courtyard. Maria can call several grannies at once. In this case, the selected grannies will go out into the courtyard at the same moment of time.
She cannot deceive grannies, that is, the situation when the i-th granny in the moment of appearing in the courtyard, finds that now there are strictly less than ai other grannies (except herself, but including Maria), is prohibited. Please note that if several grannies appeared in the yard at the same time, then each of them sees others at the time of appearance.
Your task is to find what maximum number of grannies (including herself) Maria can collect in the courtyard for the ceremony. After all, the more people in one place during quarantine, the more effective the ceremony!

Consider an example: if n=6 and a=[1,5,4,5,1,9], then:

at the first step Maria can call grannies with numbers 1 and 5, each of them will see two grannies at the moment of going out into the yard (note that a1=1≤2 and a5=1≤2);
at the second step, Maria can call grannies with numbers 2, 3 and 4, each of them will see five grannies at the moment of going out into the yard (note that a2=5≤5, a3=4≤5 and a4=5≤5);
the 6-th granny cannot be called into the yard — therefore, the answer is 6 (Maria herself and another 5 grannies).
Input
The first line contains a single integer t (1≤t≤104) — the number of test cases in the input. Then test cases follow.

The first line of a test case contains a single integer n (1≤n≤105) — the number of grannies (Maria is not included in this number).

The second line contains n integers a1,a2,…,an (1≤ai≤2⋅105).

It is guaranteed that the sum of the values n over all test cases of the input does not exceed 105.

Output
For each test case, print a single integer k (1≤k≤n+1) — the maximum possible number of grannies in the courtyard.

Example
inputCopy
4
5
1 1 2 2 1
6
2 3 4 5 6 7
6
1 5 4 5 1 9
5
1 2 3 5 6
outputCopy
6
1
6
4
Note
In the first test case in the example, on the first step Maria can call all the grannies. Then each of them will see five grannies when they come out. Therefore, Maria and five other grannies will be in the yard.

In the second test case in the example, no one can be in the yard, so Maria will remain there alone.

The third test case in the example is described in the details above.

In the fourth test case in the example, on the first step Maria can call grannies with numbers 1, 2 and 3. If on the second step Maria calls 4 or 5 (one of them), then when a granny appears in the yard, she will see only four grannies (but it is forbidden). It means that Maria can’t call the 4-th granny or the 5-th granny separately (one of them). If she calls both: 4 and 5, then when they appear, they will see 4+1=5 grannies. Despite the fact that it is enough for the 4-th granny, the 5-th granny is not satisfied. So, Maria cannot call both the 4-th granny and the 5-th granny at the same time. That is, Maria and three grannies from the first step will be in the yard in total.

题意:
Maria有n个朋友，每个朋友都有一个a[i]作为区分， 她想叫他们到家里玩，现有一个规则:
如果比我早来或和我同时来的其他朋友的数量大于或等于ai，我就同意来。
请注意，盆友们可以在同一时间进入院子，而且Maria一直在院子里等待着
问院子里最多能有多少人

思路：
肯定是优先让a[i]小的朋友先来家里，所以需要升序排列一下，然后我们发现只要 i 是大于 a[i] 的，那么前i个人都可以到家里去，找到满足上述情况的最大的i，然后加上Maria就得出答案了

代码：

#include
#include
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
	int t;
	cin >> t;
	int n;
	while (t--)
	{
		int ans = 0;
		cin >> n;
		for (int i = 1; i <= n; i++)
			cin >> a[i];
		sort(a + 1, a + 1 + n);
		for (int i = 1; i <= n; i++)
		{
			if (i>=a[i])ans = i;//标记
		}
		cout << ans+1 << endl;
	}
	return 0;
}

C. Celex Update

来源：http://codeforces.com/contest/1358/problem/C

During the quarantine, Sicromoft has more free time to create the new functions in “Celex-2021”. The developers made a new function GAZ-GIZ, which infinitely fills an infinite table to the right and down from the upper left corner as follows:

The cell with coordinates (x,y) is at the intersection of x-th row and y-th column. Upper left cell (1,1) contains an integer 1.
The developers of the SUM function don’t sleep either. Because of the boredom, they teamed up with the developers of the RAND function, so they added the ability to calculate the sum on an arbitrary path from one cell to another, moving down or right. Formally, from the cell (x,y) in one step you can move to the cell (x+1,y) or (x,y+1).

After another Dinwows update, Levian started to study “Celex-2021” (because he wants to be an accountant!). After filling in the table with the GAZ-GIZ function, he asked you to calculate the quantity of possible different amounts on the path from a given cell (x1,y1) to another given cell (x2,y2), if you can only move one cell down or right.

Formally, consider all the paths from the cell (x1,y1) to cell (x2,y2) such that each next cell in the path is located either to the down or to the right of the previous one. Calculate the number of different sums of elements for all such paths.

Input
The first line contains one integer t (1≤t≤57179) — the number of test cases.

Each of the following t lines contains four natural numbers x1, y1, x2, y2 (1≤x1≤x2≤109, 1≤y1≤y2≤109) — coordinates of the start and the end cells.

Output
For each test case, in a separate line, print the number of possible different sums on the way from the start cell to the end cell.

Example
inputCopy
4
1 1 2 2
1 2 2 4
179 1 179 100000
5 7 5 7
outputCopy
2
3
1
1
Note
In the first test case there are two possible sums: 1+2+5=8 and 1+3+5=9.

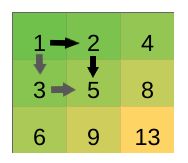
题意：
给你两个坐标，问你从（x1，y1）到（x2，y2）一共有多少条路径。
注意是在以（x1，y1）为左上角（x2，y2）为右下角构成的矩形中，而且每一步都只能向下或者向右

思路:
一开始还以为是dp的题目，后来好好想了一下应该是找规律的题目，然后就开始分析样例找规律，最后找到一个正确的，详见代码
规律:

• 若是矩形只有一行或者一列，只有一种路径
• 有多行或者多列时，路径的个数=矩形的方格数-最下边一行方格数-最右边一行方格数-起始方格，即n * m - (y2 - y1 + x2-x1 + 2)

代码：

#include
#include
using namespace std;
const int N = 1e9;
typedef long long ll;
int main()
{
	int t;
	cin >> t;
	ll x1, y1, x2, y2;
	while (t--)
	{
		cin >> x1 >> y1 >> x2 >> y2;
		if (x1 == x2 || y1 == y2)
		{
			cout << '1' << endl;
			continue;
		}
		ll n = x2 - x1 + 1, m = y2 - y1 + 1;
		ll k = n * m - (y2 - y1 + x2-x1 + 2);
		ll ans = k + 2;
		cout << ans << endl;
	}
	return 0;
}

D. The Best Vacation

来源：http://codeforces.com/contest/1358/problem/D

You’ve been in love with Coronavirus-chan for a long time, but you didn’t know where she lived until now. And just now you found out that she lives in a faraway place called Naha.

You immediately decided to take a vacation and visit Coronavirus-chan. Your vacation lasts exactly x days and that’s the exact number of days you will spend visiting your friend. You will spend exactly x consecutive (successive) days visiting Coronavirus-chan.

They use a very unusual calendar in Naha: there are n months in a year, i-th month lasts exactly di days. Days in the i-th month are numbered from 1 to di. There are no leap years in Naha.

The mood of Coronavirus-chan (and, accordingly, her desire to hug you) depends on the number of the day in a month. In particular, you get j hugs if you visit Coronavirus-chan on the j-th day of the month.

You know about this feature of your friend and want to plan your trip to get as many hugs as possible (and then maybe you can win the heart of Coronavirus-chan).

Please note that your trip should not necessarily begin and end in the same year.

Input
The first line of input contains two integers n and x (1≤n≤2⋅105) — the number of months in the year and the number of days you can spend with your friend.

The second line contains n integers d1,d2,…,dn, di is the number of days in the i-th month (1≤di≤106).

It is guaranteed that 1≤x≤d1+d2+…+dn.

Output
Print one integer — the maximum number of hugs that you can get from Coronavirus-chan during the best vacation in your life.

Examples
inputCopy
3 2
1 3 1
outputCopy
5
inputCopy
3 6
3 3 3
outputCopy
12
inputCopy
5 6
4 2 3 1 3
outputCopy
15
Note
In the first test case, the numbers of the days in a year are (indices of days in a corresponding month) {1,1,2,3,1}. Coronavirus-chan will hug you the most if you come on the third day of the year: 2+3=5 hugs.

In the second test case, the numbers of the days are {1,2,3,1,2,3,1,2,3}. You will get the most hugs if you arrive on the third day of the year: 3+1+2+3+1+2=12 hugs.

In the third test case, the numbers of the days are {1,2,3,4,1,2,1,2,3,1,1,2,3}. You will get the most hugs if you come on the twelfth day of the year: your friend will hug you 2+3+1+2+3+4=15 times.
题意：
你有连续x天的假期，想要去找你的小女朋友玩耍，但是她那里的时间计算方式不同，一年有n个月，每个月的长度为a[i]天，且你每个月的第几天去找她你就会获得几个拥抱，问你要尽可能的获得更多的拥抱，需要哪几天去（可以跨年，但是必须连续），最多能获得多少拥抱

思路：
有点像dp中的最大子段和问题，但是其实不一样，用vector解决比较容易，详见代码

代码：

#include 
#include 
#define ll long long
using namespace std;
int main()
{
    ll n, x;
    cin >> n >> x;
    vector<ll>v(2 * n);
    for (ll i = 0; i < n; i++)
    {
        cin >> v[i]; 
        v[i + n] = v[i];
    }
    ll ans = 0;
    ll d = 0, cnt = 0;
    ll in = 0;
    for (ll i = 0; i < 2 * n; i++)
    {
        d += v[i];
        cnt += ((v[i] + 1) * v[i]) / 2;
        if (d < x)continue;
        while (d - x >= v[in]) 
        {
            d -= v[in];
            cnt -= (v[in] * (v[in] + 1)) / 2;
            in++;
        }
        ll k = d - x;
        ll val = cnt - ((k + 1) * k / 2);
        if (val > ans)ans = val;
    }
    cout << ans << endl;
    return 0;
}