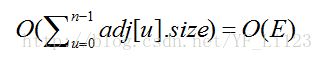C++ 求最短路径问题之Dijkstra算法（一）

求最短路径之Dijkstra算法

Dijkstra算法是用来求单源最短路径问题，即给定图G和起点s，通过算法得到s到达其他每个顶点的最短距离。

基本思想：对图G(V,E)设置集合S，存放已被访问的顶点，然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点（记为u），访问并加入集合S。之后，令u为中介点，优化起点s与所有从u能够到达的顶点v之间的最短距离。这样的操作执行n次（n为顶点个数），直到集合S已经包含所有顶点。

Dijkstra算法伪代码：

//G为图；数组d为源点到达各点的最短路径长度，s为起点
Dijkstra(G, d[], s)
{
     初始化;
     for(循环n次)
     {
          u = 使d[u]最小的还未被访问的顶点的标号;
          记u已被访问;
          for(从u出发能到达的所有顶点v)
          {
               if(v未被访问 && 以u为中介点使s到顶点v的最短距离d[v]更优)
               {
                    优化d[v];
               }
          }
     }
}

由于图可以使用邻接矩阵或者邻接表来实现，因此会有两种写法。以下图为例来具体实现代码：

（1）邻接矩阵版

const int INF = 1000000000;

/*Dijkstra算法解决的是单源最短路径问题，即给定图G(V,E)和起点s(起点又称为源点),
求从起点s到达其它顶点的最短距离，并将最短距离存储在矩阵d中*/
void Dijkstra(int n, int s, vector> G, vector& vis, vector& d)
{
       /*
       param
       n：           顶点个数
       s：           源点
       G：           图的邻接矩阵
       vis：         标记顶点是否已被访问
       d：           存储源点s到达其它顶点的最短距离
       */
       fill(d.begin(), d.end(), INF);                         //初始化最短距离矩阵，全部为INF
       d[s] = 0;                                              //起点s到达自身的距离为0
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                     //找到d[u]最小的u
              int MIN = INF;                                  //记录最小的d[u]
              for (int j = 0; j < n; ++j)                     //开始寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           u = j;
                           MIN = d[j];
                     }
              }
              //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
              if (u == -1)
                     return;
              vis[u] = true;                                  //标记u已被访问
              for (int v = 0; v < n; ++v)
              {
                     //遍历所有顶点，如果v未被访问&&u能够到达v&&以u为中介点可以使d[v]更优
                     if (vis[v] == false && d[u] + G[u][v] < d[v])
                           d[v] = d[u] + G[u][v];             //更新d[v]
              }
       }
}

复杂度分析：主要是外层的循环O(V)（V就是顶点个数n）与内层循环（寻找最小的d[u]需要O(V)、枚举需要O(V)产生的），总的时间复杂度为O(V*(V+V))=O(V^2)

(2)邻接表版

const int INF = 1000000000;

struct Node
{
       int v;         //边的目标顶点
       int dis;       //dis为边权
       Node(int x, int y) :v(x), dis(y) {}
};

void Dijkstra(int n, int s, vector> Adj, vector vis, vector& d)
{
       /*
       param
       n：      顶点个数
       s：      起点
       Adj：    图的邻接表
       vis：    标记顶点是否被访问
       d：      存储起点s到其他顶点的最短距离
       */
       fill(d.begin(), d.end(), INF);
       d[s] = 0;                                             //起点s到达自身的的距离为0
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                    //找到d[u]中最小的u
              int MIN = INF;                                 //找到最小的d[u]
              for (int j = 0; j < n; ++j)                    //寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           u = j;
                           MIN = d[j];
                     }
              }
              //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
              if (u == -1)
                     return;
              vis[u] = true;                                //标记u被访问
              for (int j = 0; j < Adj[u].size(); ++j)
              {
                     int v = Adj[u][j].v;                   //通过邻接表获取u能直接到达的v
                     if (vis[v] == false && d[v] > d[u] + Adj[u][j].dis)     
                           d[v] = d[u] + Adj[u][j].dis;       //优化d[u]
              }
       }
}

时间复杂度分析：复杂度分析：主要是外层的循环O(V)（V就是顶点个数n）与内层循环（寻找最小的d[u]需要O(V)、枚举需要O(V)产生的），又由于对整个程序来说，枚举V的次数总共为

总的时间复杂度为O(V^2+E)

总结：上面的做法都是复杂度为O(V^2)级别的，其中由于必须把每个顶点都标记已访问，因此外层循环的O(V)时间是无法避免的，但是寻找最小d[u]的过程却可以不必达到O(V)的复杂度，而可以使用对优化来降低复杂度。最简单的写法是直接使用STL中的优先队列priority_queue，这样使用邻接表实现Dijkstra算法的时间复杂度可以降低为O(VlogV+E)。此外，Dijkstra算法只能应对所有边权都是非负数的情况，如果边权出现负数，那么Dijkstra算法很可能会出错，这是最好使用SPFA算法。

(3)、如果题目给出的是无向边（即双向边）而不是有向边，又该如何解决呢？其实很简单，只需要把无向边当成两条指向相反的有向边即可。对邻接矩阵来说，一条u与v之间的无向边在输入时可以分别对G[u][v]和G[v][u]赋以相同的边权；而对于邻接表来说，只需要在u的邻接表Adj[u]末尾添加上v，并在v的邻接表Adj[v]末尾添加上u即可。

(4)、前面一直是讲解最短距离的求解，但是还没有讲到最短路径本身怎么求解。

在Dijkstra算法的伪代码部分，有这么一段：

if(v未被访问 && 以u为中介点可以使起点s到顶点v的最短距离d[v]更优){
     优化d[v];
}

"以u为中介点可以使起点s到顶点v的最短距离d[v]更优"这句话隐含了这样一层意思：使d[v]变得更小的方案是让u作为从s到v最短路径上v的前一个结点（即s->......->u->v）。于是我们不妨利用这个信息，把这个信息记录下来，设置一个数组pre[]，令pre[v]表示从起点s到顶点v的最短路径上v的前一个顶点（即前驱节点）的编号，这样就可以把每一个顶点的前驱节点记录下来。而在伪代码部分只需要在if内增加一行：

if(v未被访问 && 以u为中介点可以使起点s到顶点v的最短距离d[v]更优){
     优化d[v];
     令v的前驱为u;
}

以上图的邻接矩阵为例，代码如下：

#include 
#include 
using namespace std;

const int INF = 1000000000;

/*Dijkstra算法解决的是单源最短路径问题，即给定图G(V,E)和起点s(起点又称为源点),
求从起点s到达其它顶点的最短距离，并将最短距离存储在矩阵d中*/
void Dijkstra(int n, int s, vector> G, vector& vis, vector& d, vector& pre)
{
       /*
       param
       n：           顶点个数
       s：           源点
       G：           图的邻接矩阵
       vis：         标记顶点是否已被访问
       d：           存储源点s到达其它顶点的最短距离
       pre：         存储从起点s到达顶点v的最短路径上v的前一个顶点 （新添加）
       */
       fill(d.begin(), d.end(), INF);                         //初始化最短距离矩阵，全部为INF

       for (int i = 0; i < n; ++i)                            //新添加
              pre[i] = i;

       d[s] = 0;                                              //起点s到达自身的距离为0
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                     //找到d[u]最小的u
              int MIN = INF;                                  //记录最小的d[u]
              for (int j = 0; j < n; ++j)                     //开始寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           u = j;
                           MIN = d[j];
                     }
              }
              //找不到小于INF的d[u]，说明剩下的顶点和起点s不连通
              if (u == -1)
                     return;
              vis[u] = true;                                  //标记u已被访问
              for (int v = 0; v < n; ++v)
              {
                     //遍历所有顶点，如果v未被访问&&u能够到达v&&以u为中介点可以使d[v]更优
                     if (vis[v] == false && d[u] + G[u][v] < d[v]) {
                           d[v] = d[u] + G[u][v];             //更新d[v]
                           pre[v] = u;                        //记录v的前驱顶点为u（新添加）
                     }
              }
       }
}

//输出从起点s到顶点v的最短路径
void DFSPrint(int s, int v, vector pre)
{
       if (v == s) {
              cout << s << " ";
              return;
       }
       DFSPrint(s, pre[v], pre);
       cout << v << " ";
}

void main()
{
       int n = 6;
       vector> G = { {0,1,INF,4,4,INF},
                                 {INF,0,INF,2,INF,INF},
                                 {INF,INF,0,INF,INF,1},
                                 {INF,INF,2,0,3,INF},
                                 {INF,INF,INF,INF,0,3},
                                 {INF,INF,INF,INF,INF,0} };
       vector vis(n);
       vector d(n);
       vector pre(n);

       Dijkstra(n,0,G,vis,d,pre);
       for (auto x : d)
              cout << x << " ";
       cout << endl;

       //输出从起点s到顶点v的最短路径
       DFSPrint(0, 5, pre);
}