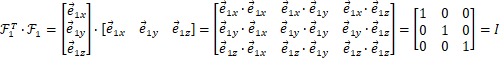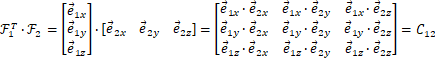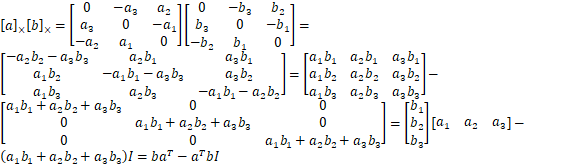视觉SLAM中的李群和李代数学习笔记(一)
视觉SLAM中的李群和李代数学习笔记
本文基于《State Estimation for Robotics》和《视觉SLAM十四讲》以及维基百科相关条目,用于个人学习总结和记录备忘,同时分享出来与大家共同交流和探讨。文章内容仅代表个人理解,如有不当之处请大家批评指正。此外,关于视觉SLAM中的李群和李代数的经典讲解请阅读高翔博士的《视觉SLAM十四讲》和一系列博客,本文重点关注数学推导,仅为本人喜欢追究数学推导而写。
1. 三维空间中的位姿表示
首先谈谈为什么要在视觉SLAM中讨论李群和李代数,同时为了更好地理解和推导,首先要回顾一下三维空间的位姿表示。考虑将同一个空间向量在两个不同的坐标系中进行表示,首先假设两个坐标系的原点重合,有
其中![]() 和
和![]() 分别是坐标系1和2的基,而
分别是坐标系1和2的基,而![]() 和
和![]() 分别为
分别为![]() 在两个坐标系中的坐标。现在要对两个坐标表示进行转换,由
在两个坐标系中的坐标。现在要对两个坐标表示进行转换,由
![]()
可得
![]()
而
其中在![]() 和
和![]() 中为了方便省略了对基向量的转置上标而用
中为了方便省略了对基向量的转置上标而用![]() 表示向量内积,而对于
表示向量内积,而对于![]() 和
和![]() 来说
来说![]() 为一般的矩阵乘积。所以
为一般的矩阵乘积。所以
![]()
其中![]() 为三维旋转矩阵,为正交矩阵,满足
为三维旋转矩阵,为正交矩阵,满足
![]()
![]()
同时反过来有
![]()
可以看出,旋转矩阵![]() 由坐标系1的基向量分别与坐标系2的每个基向量的内积作为一行构成(由于基向量的长度为1,也就是说
由坐标系1的基向量分别与坐标系2的每个基向量的内积作为一行构成(由于基向量的长度为1,也就是说![]() 的每一行是将坐标系1的基向量用坐标系2的基进行表示),用来将坐标系2中的向量坐标转换到坐标系1中。
的每一行是将坐标系1的基向量用坐标系2的基进行表示),用来将坐标系2中的向量坐标转换到坐标系1中。
当两个坐标系的原点不重合时,设向量![]() 的终点为
的终点为![]() ,有
,有
![]()
在坐标系1中表示为
![]()
其中![]() 为向量
为向量![]() 在坐标系1中的坐标表示,其他各项类似。同时在上式中,
在坐标系1中的坐标表示,其他各项类似。同时在上式中,![]() 为点
为点![]() 在坐标系2中的坐标,而
在坐标系2中的坐标,而![]() 为点
为点![]() 在坐标系1中的坐标,上式表明了三维空间坐标在不同坐标系中的转换关系,写成矩阵乘积形式为
在坐标系1中的坐标,上式表明了三维空间坐标在不同坐标系中的转换关系,写成矩阵乘积形式为
其中空间坐标用齐次坐标的形式表示,而
为齐次变换矩阵。
将齐次变换矩阵与一般的![]() 矩阵相比较,可以看出其具有特殊的形式,最后一行为
矩阵相比较,可以看出其具有特殊的形式,最后一行为![]() ,左上角
,左上角![]() 的分块为正交矩阵。也就是说,一个
的分块为正交矩阵。也就是说,一个![]() 矩阵要成为齐次变换矩阵,必须满足最后一行为
矩阵要成为齐次变换矩阵,必须满足最后一行为![]() 和左上角
和左上角![]() 的分块为正交矩阵的约束。在视觉SLAM中经常要对相机的位姿,即齐次变换矩阵进行非线性优化,而一般的非线性优化算法是针对普通的矩阵的,在对位姿进行优化时要加上以上各项约束,以使得优化得到的结果为有效的齐次变换矩阵。然而在非线性优化中处理这些约束条件比较不方便,所以要引入李代数来对齐次变换矩阵进行表示,位姿的李代数可以用一个任意的6维向量来表示,不需要满足任何的额外约束,于是可以将约束优化问题转化为无约束优化问题。所以讨论李群和李代数并采用李代数进行表示简单地说就是为了方便进行非线性优化。
的分块为正交矩阵的约束。在视觉SLAM中经常要对相机的位姿,即齐次变换矩阵进行非线性优化,而一般的非线性优化算法是针对普通的矩阵的,在对位姿进行优化时要加上以上各项约束,以使得优化得到的结果为有效的齐次变换矩阵。然而在非线性优化中处理这些约束条件比较不方便,所以要引入李代数来对齐次变换矩阵进行表示,位姿的李代数可以用一个任意的6维向量来表示,不需要满足任何的额外约束,于是可以将约束优化问题转化为无约束优化问题。所以讨论李群和李代数并采用李代数进行表示简单地说就是为了方便进行非线性优化。
2. 叉积
在李群和李代数的讨论中要大量地用到三维向量的叉积运算,所以先对向量叉积的一些性质进行讨论。
设![]() ,
,![]() ,
,![]() ,则
,则
其中
为反对称矩阵,![]() ,同时
,同时![]() 还有许多其他的符号表示如
还有许多其他的符号表示如![]() 和
和![]() 等,均与上式相同。叉积的基本性质详见维基百科,下面仅列举其中几条。
等,均与上式相同。叉积的基本性质详见维基百科,下面仅列举其中几条。
![]()
![]()
![]()
![]()
![]()
![]() (BAC-CAB法则)
(BAC-CAB法则)
那么有
特别地有![]()
此外,若![]() ,则
,则![]()
接下来证明![]() 为线性运算,即
为线性运算,即![]() ,有
,有
由于![]() 为线性运算,对
为线性运算,对![]() 的处理可以很方便地进行,例如
的处理可以很方便地进行,例如
![]()
成立,或者是可以反方向进行。其实![]() 的线性性质也可以由叉积的分配律得到,此处略。
的线性性质也可以由叉积的分配律得到,此处略。
最后,考虑一个与后面李括号运算相关的问题
![]()
所以如果将反对称阵分别表示为![]() 和
和![]() ,定义李括号运算
,定义李括号运算![]() ,则有
,则有
![]()
![]()
![]()
以此类推。
3. 李群和李代数定义
此处照抄《视觉SLAM十四讲》中给出的讲解。“群”是由一个集合加上一种运算构成的代数结构,如果把集合记作![]() ,运算记作
,运算记作 ![]() ,那么群可以表示成
,那么群可以表示成![]() ,并且要求运算满足以下条件
,并且要求运算满足以下条件
- 封闭性:
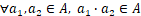
- 结合性:
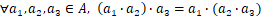
- 单位元:
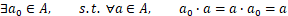
- 逆 元:

李群是具有连续(光滑)性质的群。后面要讨论的李群有:特殊正交群![]() ,特殊欧式群
,特殊欧式群![]() ,以及特殊欧式群
,以及特殊欧式群![]() 的伴随
的伴随![]() 。前面提到的旋转矩阵
。前面提到的旋转矩阵![]() ,齐次变换矩阵
,齐次变换矩阵![]() ,由于三维空间中刚体旋转和平移运动都是连续的,所以
,由于三维空间中刚体旋转和平移运动都是连续的,所以![]() 和
和![]() 都是李群。
都是李群。
李代数由一个向量空间![]() ,一个数域
,一个数域![]() 和一个二元运算
和一个二元运算![]() 组成,表示为
组成,表示为![]() 。其中二元运算
。其中二元运算![]() 称为李括号,要求满足以下条件
称为李括号,要求满足以下条件
- 封闭性:

- 双线性:
 ,
,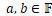 ,
,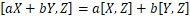 ,
,
- 自反性:

- 雅可比等价:
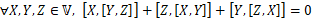
根据前面关于叉积的讨论,![]() 就构成一个李代数。后面要讨论的李代数有:
就构成一个李代数。后面要讨论的李代数有:![]() ,
,![]() 和
和![]() ,分别与
,分别与![]() ,
,![]() 和
和![]() 相对应。
相对应。
4. 特殊正交群![]() 和李代数
和李代数![]()
特殊正交群用来表示空间旋转,为旋转矩阵的集合
![]()
定义![]() 上的运算为普通的矩阵乘法运算,则满足
上的运算为普通的矩阵乘法运算,则满足
- 封闭性:
 ,
,
- 结合性:
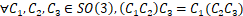
- 单位元:

- 逆 元:
 ,
, ,
,
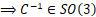 ,
,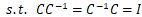
同时由空间旋转的连续性可知![]() 连续,所以
连续,所以![]() 为李群。与
为李群。与![]() 相关联的李代数
相关联的李代数![]() 定义为
定义为
向量空间:![]()
数域:![]()
李括号:![]()
可以验证李代数的各条性质,设![]()
- 封闭性:
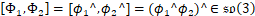
- 双线性:
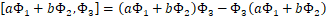
 ,类似有
,类似有 
- 自反性:
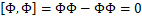
- 雅可比等价:

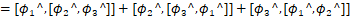
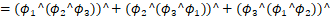
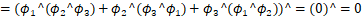
其中反复用到了![]() ,
,![]() 为线性运算,并且最后一步
为线性运算,并且最后一步![]() 可以由叉积的性质
可以由叉积的性质![]() 得到。
得到。
接下来考虑![]() 与
与![]() 的对应关系,由指数映射给出
的对应关系,由指数映射给出
其中![]() ,
,![]() ,
,![]() 。令
。令
那么有![]() ,又
,又
![]()
![]()
所以
![]()
即
![]()
由于对任意正整数![]() ,有
,有![]() ,
,![]() ,所以有
,所以有
![]()
即存在无穷多个![]() 对应到同一个
对应到同一个![]() ,所以从
,所以从![]() 是多对一的映射关系,
是多对一的映射关系,![]() 是满射但不是单射 。而如果限制
是满射但不是单射 。而如果限制![]() ,则每个
,则每个![]() 只能由一个
只能由一个![]() 得到。
得到。
反过来,从![]() 的映射记作对数映射
的映射记作对数映射![]() ,但是一般不直接用定义
,但是一般不直接用定义![]() 计算。由于
计算。由于
所以有
![]()
通常取![]() 。另一方面,由于
。另一方面,由于![]() 为旋转矩阵
为旋转矩阵![]() 对应的旋转轴,所以对
对应的旋转轴,所以对![]() 进行旋转其方向保持不变,即有
进行旋转其方向保持不变,即有
![]()
通过求解旋转矩阵![]() 的特征值1对应的单位特征向量可以求得
的特征值1对应的单位特征向量可以求得![]() ,最后由
,最后由![]() 得到
得到![]() ,完成从
,完成从![]() 的映射。
的映射。
暂时先写到这里吧,剩下特殊欧式群![]() 和李代数
和李代数![]() ,
,![]() 和
和![]() ,以及BCH公式和李代数求导等内容放到下一篇继续。
,以及BCH公式和李代数求导等内容放到下一篇继续。