黎曼猜想(三)黎曼猜想
黎曼猜想(三)黎曼猜想
- 黎曼函数的由来
- 素数定理
- 黎曼函数
- 黎曼猜想
- 黎曼猜想的后继故事
- 进展
- 感想
黎曼函数的由来
到了这里,我们可以看出了 ε ( s ) \varepsilon(s) ε(s)和素数存在了千丝万缕的关系,于是人们认为 ε ( s ) \varepsilon(s) ε(s)可能是破解素数规律的至强法宝,在了解黎曼函数与素数的关系之前,我们先来看看素数的分布规律。
素数定理
了解素数定理之前,先了解素数的分布规律,统计一下一段里素数的个数。如下图所示:
[ 1 − 10 4 1 − 100 25 1 − 1000 168 . . . . . . . . ] \left[ \begin{array}{cc|c} 1-10&&4 \\ 1-100&&25 \\ 1-1000&&168 \\ ....&&.... \end{array} \right] ⎣⎢⎢⎡1−101−1001−1000....425168....⎦⎥⎥⎤
后来有人想,有没有一个式子,通过给定的x能求出小于x的素数的个数,最早给出这个答案就是高斯大神!
据说高斯15岁的时候给出了这么一个猜想:对于给定的自然数x,小于x的素数的个数约等于 x ln x \frac{x}{\ln{x}} lnxx个,但是高斯没有高调地发表出来。
后来是同时期的数学家勒让德公布出了这个结果,是当时3L大数学家——拉格朗日、勒让德、拉普拉斯之一。
但是人们一听说高斯早就发现了这个公式,那这个功劳就揣在高斯的口袋里了,哈哈哈。
素数定理:
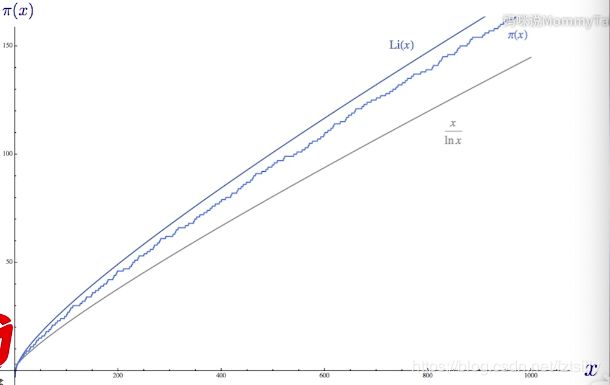
设x≥1,以π(x)表示不超过x的素数的个数,当x→∞时, π ( x ) \pi(x) π(x)~ L i ( x ) Li(x) Li(x)(对数积分函数)或 π ( x ) \pi(x) π(x)~ x l n ( x ) \frac{x}{ln(x)} ln(x)x(素数计数函数)。
即:
π ( x ) ~ x ln x 或 L i ( x ) = ∫ 2 x d t ln t \pi(x) ~ \frac{x}{\ln{x}} 或 Li(x) = \int_{2} ^{x}{\frac{dt}{\ln{t}}} π(x)~lnxx或Li(x)=∫2xlntdt
x越大,误差越小,但还是存在误差项
中间是最准确的素数计数函数,但是看起来 L i ( x ) Li(x) Li(x)比 π ( x ) \pi(x) π(x)更准确一点,但两个函数都不能准确地描述素数分布的规律,这时,高斯的学生黎曼出现了!!!
黎曼在欧拉的基础上把 ε \varepsilon ε函数进行了解析延拓就称为黎曼 ζ \zeta ζ函数,之前提到过s是必须要大于1的,才是收敛,才是有意义的,s小于1是发散的,是无意义的。
那黎曼就想,能不能通过办法,让s在所有的复数域都具有意义,这个方法就是解析延拓。最后黎曼得出来,在所有的复平面内,只有1一个奇点没有意义,其他点都具有意义,也就是都是收敛的。所以这个拓展了定义域之后,这个函数就叫黎曼 ζ \zeta ζ函数。并且黎曼通过这个函数提出了著名的黎曼猜想。
(关于解析延拓可看上篇博客)
最终,在黎曼当上了柏林的科学院通讯院士,为了回应这个荣誉,黎曼发表了一篇8页的论文《论小于某给定数值的素数个数》。从此黎曼函数横空出世。
黎曼函数
黎曼 ζ \zeta ζ函数主要是研究素数分布的情况才出现的。
先来看一下 ζ ( x ) \zeta(x) ζ(x)的函数式:
ζ ( s ) = 1 + 1 2 s + 1 3 s + 1 4 s + . . . \zeta(s) = 1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \frac{1}{4^{s}}+... ζ(s)=1+2s1+3s1+4s1+...
在来看一下黎曼 ζ \zeta ζ函数经过解析延拓后的积分形式:
ζ ( x ) = Γ ( 1 − s ) 2 π i ∮ r z s − 1 e − z 1 − e z d z \zeta(x) = \frac{\Gamma (1-s)}{2\pi i}\oint_r\frac{z^{s-1}e^{-z}}{1-e^{z}} dz ζ(x)=2πiΓ(1−s)∮r1−ezzs−1e−zdz
这个函数又被称为亚纯函数。
其中 Γ ( s ) \Gamma (s) Γ(s)(伽马函数)就是表示 ( s − 1 ) ! (s-1)! (s−1)!(阶乘)。
(这个式子只能看看就好,常人无法理解,卑微的我更无法理解)
这样,黎曼就把欧拉级数的定义域从s>1通过解析延拓将其扩大,扩大到除了1这一个奇点外的所有复平面内。(复数都知道吧,不单是实数,虚数也可以)
先尝试带几个数进去看看。
ζ ( − 1 ) = − 1 12 ζ ( − 2 ) = 0 ζ ( − 3 ) = 1 120 \zeta(-1)=-\frac{1}{12}\\ \zeta(-2) = 0\\ \zeta(-3) = \frac{1}{120} ζ(−1)=−121ζ(−2)=0ζ(−3)=1201
黎曼通过解析延拓出来的结果和欧拉当时算出来的结果是相同的。那么黎曼猜想是怎么来的呢?
然后就到了今天的主题——黎曼猜想。
黎曼猜想
黎曼通过把黎曼 ζ \zeta ζ函数推导后,得出下面的式子:
ζ ( s ) = 2 Γ ( 1 − s ) ( 2 π ) s − 1 sin ( π s 2 ) ζ ( 1 − s ) \zeta(s) = 2\Gamma (1-s)(2\pi)^{s-1}\sin(\frac{\pi s}{2})\zeta(1-s) ζ(s)=2Γ(1−s)(2π)s−1sin(2πs)ζ(1−s)
肉眼可见,上面式子中令 sin ( π s 2 ) = 0 \sin(\frac{\pi s}{2})=0 sin(2πs)=0就得到了一些函数零点,比如-2,-4,-6…这些个零点被称为平凡零点。
然后我们让上面式子强行等于0,就是求 ζ ( s ) \zeta(s) ζ(s)除了平凡零点外的非平凡零点,那么黎曼猜想就来了。
黎曼猜测,所有的非平凡零点的实部都在 x = 0 x = 0 x=0和 x = 1 x = 1 x=1这两条临界线之内,这一块区域叫做临界区域或者关键区域。有可能零点的实部都在 x = 1 2 x = \frac{1}{2} x=21这条临界线上。但是黎曼无法证明。
而黎曼 ζ \zeta ζ函数的零点又与素数的分布情况紧密相连,所以,如果有人能证实黎曼猜想,这将是轰动全球的大事件。
黎曼猜想的后继故事
在1900年国际数学大会上,希尔伯特在演讲中提出了23个数学问题,其中第八个就是黎曼猜想,与他并列第八的就是哥德巴赫猜想。
在2000年的千禧年,美国的克雷数学研究所提出了7个
千禧难题,全是数学猜想,其中黎曼猜想就在其中,只要能证明其中一个就能拿到100万美元,其中的庞加莱猜想已经被证明了。这个人会是你吗?
进展
1896年法国的两个学者阿达玛和普森两个人证明了所有的非平凡零点的实部都在 x = 0 x = 0 x=0和 x = 1 x = 1 x=1这两条临界线里;
1932年,黎曼-西格尔公式出世,以后计算零点的方法要方便得多。
后来通过计算机,德国的IBM实验室(项目现在已经取消了),已经计算出了有了1万亿个非平凡零点,而这些非平凡零点都在 x = 1 2 x = \frac{1}{2} x=21这条线上。
感想
最后,花了一周的时间来写这几篇博客,以前就想写这方面的博客,这次终于完结了,其实写这些东西对我来说没有太多的帮助,这只是出于对数学的兴趣(其实我数学很垃圾),爱好使然吧!
不得不说这些人的智慧是非比寻常的。那就来看看黎曼的人生事迹:
https://www.bilibili.com/video/BV1xE411u7Zp
参考:
https://www.bilibili.com/video/BV1oW411U7Bk?t=589
https://www.bilibili.com/video/BV1rW411m7GL
https://www.bilibili.com/video/BV12x41187QH?from=search&seid=17055570753699382374