C. Instant Noodles（gcd 数学 哈希）

http://codeforces.com/problemset/problem/1322/C

题意：

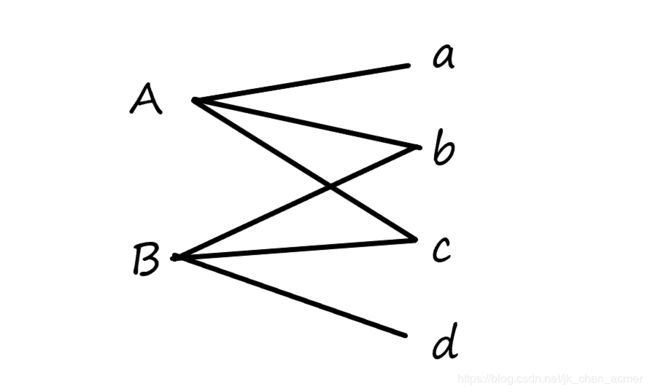
二分图，两边都是n个点，右边的点有点权。对于左边的点集$S$，与点集中点相连的右边的点集$S^{\prime }$，权值之和为$Val(S^{\prime })$。

对于所有的可能$S$，求$GCD(Val(S^{\prime }))$。

解析：

我们分析下面的图

答案为：$GCD(a+b+c,b+c+d,a+b+c+d)$

辗转相减后得到：$GCD(a,b+c,d)$

分析就可以得到结论：对于右边的点，若两个点（这里的b和c）连接的点集相同（AB），则这两个点为一类点。

结果答案为所有类点内部权值和的gcd。

而分析哪些点为一类用哈希即可。

代码：

/*
 *  Author : Jk_Chen
 *    Date : 2020-07-12-09.43.46
 */
#include
using namespace std;
#define LL long long
#define rep(i,a,b) for(int i=(int)(a);i<=(int)(b);i++)
#define per(i,a,b) for(int i=(int)(a);i>=(int)(b);i--)
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define pill pair
#define fi first
#define se second
void test(){cerr<<"\n";}
template<typename T,typename... Args>void test(T x,Args... args){cerr<<"> "<<x<<" ";test(args...);}
const LL mod=1e9+7;
const int maxn=5e5+9;
const int inf=0x3f3f3f3f;
LL rd(){ LL ans=0; char last=' ',ch=getchar();
    while(!(ch>='0' && ch<='9'))last=ch,ch=getchar();
    while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans; return ans;
}
#define rd rd()
/*_________________________________________________________begin*/

LL a[maxn];
vector<int>V[maxn];
pair<LL,int> hs[maxn];

void add(int a,int b){
    V[b].pb(a);
}

int main(){
    LL M=100000ll;
    M*=100000ll;
    M+=7;
    int _=rd;while(_--){
        int n=rd,m=rd;
        rep(i,1,n)V[i].clear(),hs[i].fi=0;
        rep(i,1,n){
            a[i]=rd;
        }
        rep(i,1,m){
            int a=rd,b=rd;
            add(a,b);
        }
        rep(i,1,n)sort(V[i].begin(),V[i].end());
        rep(i,1,n){
            for(auto P:V[i]){
                hs[i].fi=(hs[i].fi*M+P)%1000007ll;
            }
            hs[i].se=i;
        }
        LL gcd=-1;
        sort(hs+1,hs+1+n);
        int l=1;
        while(hs[l].fi==0)l++;
        rep(i,l,n){
            if(i==n||hs[i].fi!=hs[i+1].fi){
                LL sum=0;
                rep(j,l,i)sum+=a[hs[j].se];
                if(gcd==-1)gcd=sum;
                else gcd=__gcd(sum,gcd);
                l=i+1;
            }
        }
        printf("%lld\n",gcd);
    }
    return 0;
}

/*_________________________________________________________end*/