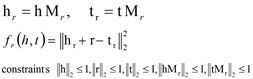基于知识图谱的表示学习——Trans系列算法介绍（一）

鉴于知识图谱的研究越来越多，所以在组会主讲上介绍了知识图谱表示学习的Trans系列方法，以下仅是本人对于此类方法的理解，请批评指正。Trans系列方法的源码均为公开代码，可以自行在GitHub中搜索。

背景介绍

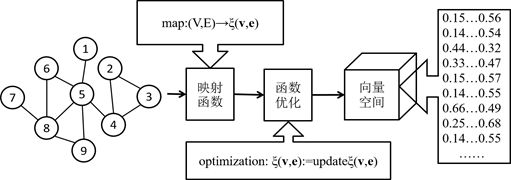
谷歌提出的知识图谱在其搜索引擎上的成功应用引起了业界的广泛关注，并迅速的成为了各行各业的研究热点。基于知识图谱的关系抽取、基于知识图谱的知识推理和基于知识图谱的问答系统的相关论文迅速占据了顶会和顶刊的版面，其中对于知识图谱的表示学习更是为这些任务提供了较底层的支持。表示学习的核心思想即挖掘数据的关键性特征，通过设计映射函数将能够充分表征原始数据的信息以一个低维的向量来表示。以网络的表示学习为例简单的说明一下，如图1所示。

                                          

                                                                                  图1.网络表示学习核心思想

网络的表示学习即在原始的网络数据中分析能够度量两个节点相似程度的属性特征，目前经典的LINE、node2vec等方法多是通过假定直接相连的节点更相似（如图1/5,5/8等）、共享更多共同邻居节点（如图6和9等）和拥有相似结构的节点（如图4、5和8等）具有相似性来设计一种将网络空间的节点映射到低维向量空间的表示函数，并通过遍历网络、负采样等方法对表示函数进行优化，从而得到一个可以基本保持原始数据特征的向量空间，即网络空间中相似的两个节点在向量空间中具有相似性（一般使用欧式距离或者cosine相似度进行度量）。

知识图谱的表示学习即将知识图谱构建成一个（头实体，关系，尾实体）的三元组形式，通过目标函数将实体和关系分别以低维的向量来表示。Trans系列的知识图谱表示方法均采用同样的函数思想，即|h + r| ≈ t，其中h, t分别表示知识图谱中的头实体和尾实体的向量表示，r表示为关系的向量表示。Trans方法主要有TransE、TransH、TransR、CtransR、TransD、TransA以及TransG等。

Trans系列算法

TransE: “Translating Embeddings for Modeling Multi-relational Data” (NIPS2013)

动机：TransE算法是早期知识图谱表示学习的典型算法。该算法设计的动机源于作者对于知识库的分层认知和自然传递表示的认识。作者认为知识图谱中的实体和关系是一层一层的进行组织的，同时实体可以通过某种传递方式得到其他实体的信息，从而可以用于对实体进行表示。同时，2013年提出了词向量的概念，并在文本数据上取得了很大的进步，而词向量就是在语料文档的词向量空间寻找相同性质的词，即C(king) – C(queen) ≈ C(man) – C(woman)。又，词向量空间中的传递是存在不变性的。受到这两点的启发，作者提出了TransE算法。

模型：给定知识图谱(h,l,t)，其中h为头实体集合，t为尾实体集合，l为关系集合。然后将实体和关系在各自的空间中（实体空间和关系空间）表示为向量，使知识图谱中的每个三元组的实体向量和关系向量满足 |h + l| ≈ t：即如果三元组是正确的，则尾实体向量应该与头实体向量和关系向量的加和更为接近；反之，如果三元组是错误的，则尾实体向量应该与头实体向量和关系向量的加和更为远离。基于此，TransE算法的目标函数设计为：

                                                              

其中，[·]+表示max(0,x)，d(·)表示一种衡量三元组能量(energy)的距离函数，可以是L1范数也可以是L2范数。Γ表示的是三元组正例和负例的间隔，为超参，类似于SVM分类算法中的“间隔”。从目标函数中可看到需要负例(h’,l,t’)来进行函数的优化。但是众所周知，知识图谱中存储的均为正例，所以就需要人为的构建负例。TransE算法使用的是如下所示的负例构建方法。

                                         

即从知识图谱中随机抽取其他头实体和尾实体来替换当前三元组中头实体或者尾实体，但是为了防止替换之后的三元组也是正例，TransE算法的限制是替换过程不能同时进行。

模型优化过程为最小化目标函数L，即时d(h+l,t)的值小，d(h’+l,t’)的值大，同时使用随机梯度下降（SGD）加速优化过程。TransE的算法主要可分为三步，如图2所示。

                                   

                                                                                              图2. TransE算法伪代码

第一步：随机初始化头实体、尾实体和关系向量，但是对随机初始化的向量做归一化处理；第二步：对数据集中的三元组抽样，并对抽样的三元组进行实体替换，形成负例；第三步：优化目标函数，得到实体和关系的向量表示。从算法描述中可以看出，TransE对于出现在一个既出现在头部又出现在尾部的实体的向量表示是没有区分的。

问题：TransE算法对知识图谱的表示学习提供了很好的研究思路，但是它只能很好的解决知识图谱中1对1的关系表示，而对于1对多，多对1和多对多的关系类型就无法很好的进行表示。同时对于有自反映射的关系也是无法解决的。比如，从TransE算法的目标函数中可以得到，当三元组为黄金三元组是，h+r-t=0, 但如果r是自反映射，则r=0，即h=t。如此，在多对1和1对多的场景中，有h0=h1=…=hm, t0=t1=…=tm。因此忽略了实体的分布表示。

TransH:“Knowledge Graph Embedding by Translatiing on Hyperplanes”(AAAI2014)

基于TranE算法的所存在的问题，TransH主要对知识图谱中实体的分布表示加以利用，将不同的实体根据不同的关系映射到超平面上进行向量表示，从而利用了实体的分布表示。

模型：TransH首先将知识图谱中的某一种关系类型映射与一个超平面中，根据超平面中的关系，将不同的实体通过映射矩阵投影到该超平面上，从而使得每一个实体都有自己的分布表示，如图3所示。（自己理解：不同的三元组关系被映射到某一个超平面上时会产生不同的关系映射向量，在此超平面上进行传递转移操作将会对不同关系下的不同实体进行区分）

                                                        

                                                                             图3. TransH 方法示意图

假设h,r和t是某一个三元组中的一个实例，将r投影到超平面上得到关系投影dr, 根据关系r的投影dr, 将h和t同样映射于该超平面上，则实体在该平面上是具有其独立的分布表示的。

论文中设置的得分函数为, 通过将关系映射到超平面||wr||2=1上，则从向量的投影公式可以得到头实体和尾实体的一个投影表示。因此得分函数可以重新被修改，具体过程如下。

                               

在优化目标函数L的过程中，与TransE一样，最小化L, 使得正例三元组的值小，负例三元组的值大。同时，为了解决TransE算法的负采样问题，TransH提出了一种新的负例生成方法，用以解决1对多和多对1的情况。

负例生成：基本原则是对于1对多的三元组，给予头实体更多的机会，对于多对一的三元组，给予尾实体更多的机会。所以论文使用一个伯努利分布来分配头尾实体的替换。tph / tph+hpt （分配头实体）& hpt / tph+hpt（分配为实体）。其中，tph表示每个尾实体的平均头实体数， hpt 表示每个头实体的平均为实体数。

问题：TransH存在的问题是虽然考虑了实体自身的分布表示，但是对实体的关系的表示依然是在同一空间（超平面空间）中进行的。可是本质上，实体和关系是相互区别的。

TransR:“Learning and Relation Embedding for Knowledge Graph Completion”(AAAI2015)

模型：TransR算法是将实体和关系分别映射到两个空间中，然后将实体空间中的实体通过转移矩阵Mr转移到关系空间中进行向量表示，在TransR算法中，每一个三元组的实体向量被设为一个k维向量，关系向量被设为一个d维向量，但是k可以不等于d，而映射矩阵则为一个k×d的矩阵, 这样在从实体空间转移到关系空间之后，每个头实体和尾实体都变成了关系空间的向量表示。如图4所示。

                             

                                                                                         图4. TransR 算法示意图

TransR的目标函数优化思想跟TransE一致。这里不再详述。论文通过分析发现TransE、TransH以及TransR对于关系的表示均是使用一个唯一的表示，但是关系本身却是一个多元的，类型丰富的。为了解决这个问题，论文提出了一种CtransR的方法。个人理解是一个近似于“词袋”的模型，将具有同性质的关系进行打包学习。

CtransR流程：首先，算法将输入的实例分割成n个组。其次，对于一种具体的关系r, 与它相关的全部实体被聚到一类，这样训练集中的全部实体都被分成n个组。然后，所有的实体对（h,t）都用其所在的组别的偏移向量（h-t）表示。最后，学习每个组的关系向量rc和转移矩阵Mr。具体的得分函数和目标函数如下所示，同样使用SGD算法进行优化。

                       

                      

问题：TransR没有考虑关系的类型问题，而CtransR是仅考虑了关系的类型问题，而没有考虑实体的类型问题。因为在通用领域中，不同的实体是属于不同的类型的。

TransD:“Knowledge Graph Embedding via Dynamic Mapping Matrix” (ACL 2015)

动机：不同类型的实体有不同的属性和作用，如果将全部实体都映射到同一空间，使用同一参数进行传递表示时不充分的。本质上应该如果是相似的实体，他们应该是具有相似的映射矩阵，反之则应该具有不相似的映射矩阵。所以本文设置了一种动态映射矩阵来对不同类型的实体和关系进行投影。

模型：对于一个实体或者关系都表示成两个向量，即h,hp,r,rp,t,tp . h,hp,t,tp ∈Rn，r,rp  ∈Rm。同时设置两个映射矩阵Mrh, Mrt ∈Rm×n。算法对原实体空间的头尾映射使用Mrh和Mrt这两个矩阵。

                                 

                                                                      图6. TransD 算法示意图

从图6中可以看出，TransD与transR的不同之处在于TransD使用的动态矩阵是可以将不同类型的实体进行区别，独立映射的。TransD的目标函数与TranR一样，因此不再赘述。

总结

总的来说，Trans系列的算法在知识图谱的表示学习上逐渐完善，但是同样存在很多未能解决的点，比如如何解决多元关系的预测问题，如何结合实体本身的属性信息等等。另外还有两项工作值得关注，TransA和TransG，目前还没有具体的发表消息，但是在arxive上可以找到。

参考文献

1. TransA: An Adaptive Approach for Knowledge Graph Embedding
2. TransG: A Generative Model for Knowledge Graph Embedding