FOC中的Clarke变换和Park变换详解(动图+推导+仿真+附件代码)
文章目录
- 1 前言
- 2 自然坐标系ABC
- 3 α β \alpha\beta αβ 坐标系
- 3.1 Clarke变换
- 3.2 Clarke反变换
- 4 d q dq dq 坐标系
- 4.1 Park变换
- 正转
- 反转
- 4.2 Park反变换
- 5 程序实现
- 附件
1 前言
永磁同步电机是复杂的非线性系统,为了简化其数学模型,实现控制上的解耦,需要建立相应的坐标系变换,即Clark变换和Park变换。
2 自然坐标系ABC
三相永磁同步电机的驱动电路如下图所示;
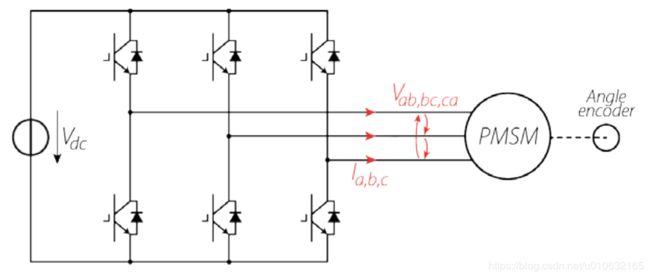
根据图示电路可以发现在三相永磁同步电机的驱动电路中,三相逆变输出的三相电压为 U A U_{A} UA, U B U_{B} UB, U C U_{C} UC将作用于电机,那么在三相平面静止坐标系ABC中,电压方程满足以下公式:
{ U A = U m c o s θ e U B = U m c o s ( θ e + 2 π 3 ) U C = U m c o s ( θ e − 2 π 3 ) \begin{cases}U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \\ U_{C} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧UA=UmcosθeUB=Umcos(θe+32π)UC=Umcos(θe−32π)
θ e \theta_{e} θe为电角度
U m U_{m} Um为相电压基波峰值
所以根据上述公式可以发现,三相电压的大小是随时间变化的正弦波形,相位依次相差120°,具体如下图所示;
3 α β \alpha\beta αβ 坐标系
由静止三相坐标系 A B C ABC ABC变换到静止坐标系 α β \alpha\beta αβ的过程称之为Clarke变换;在 α β \alpha\beta αβ静止坐标系中, α \alpha α轴和 β \beta β轴的相位差为90°,且 α β \alpha\beta αβ的大小是随时间变化的正弦波形,具体如下图所示;
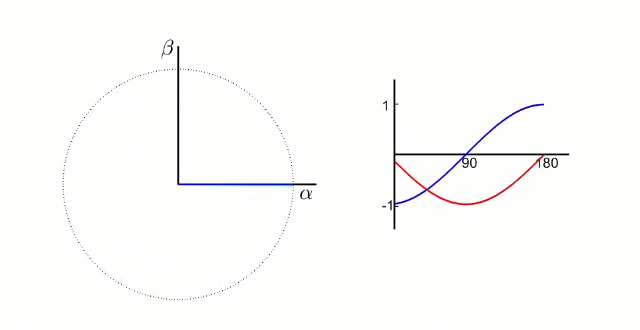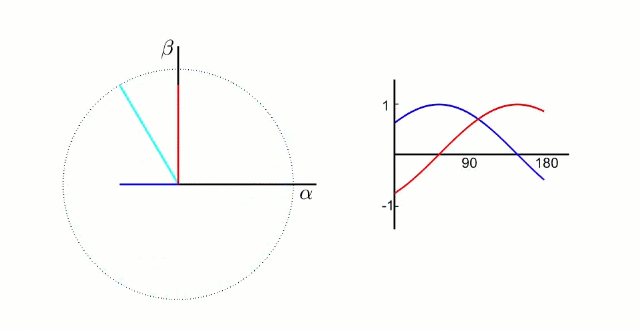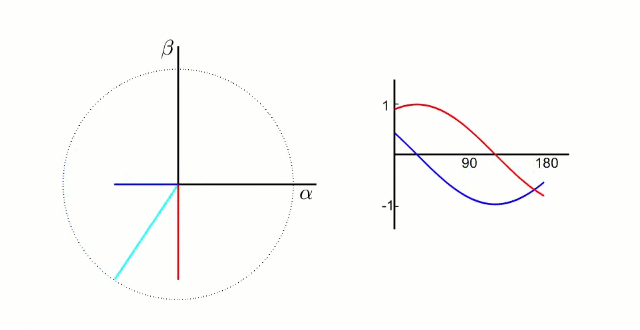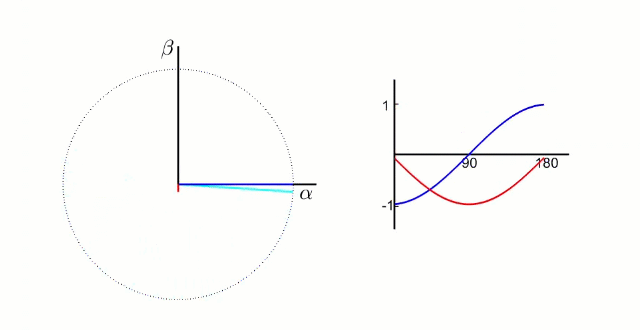
从自然坐标系 A B C ABC ABC 变换到静止坐标系 α β \alpha\beta αβ,满足以下条件:
[ f α f β f 0 ] = T 3 s / 2 s ∗ [ f A f B f C ] \begin{bmatrix} f_{\alpha} \\ f_{\beta} \\ f_{0} \end{bmatrix} = T_{3s/2s}*\begin{bmatrix} f_{A} \\ f_{B} \\ f_{C} \end{bmatrix} ⎣⎡fαfβf0⎦⎤=T3s/2s∗⎣⎡fAfBfC⎦⎤
其中 T 3 S / 2 S T_{3S/2S} T3S/2S为变换矩阵:
T 3 S / 2 S = N ∗ [ 1 − 1 2 − 1 2 0 3 2 − 3 2 2 2 2 2 2 2 ] T_{3S/2S} = N*\begin{bmatrix} 1 &-\cfrac{1}{2} &-\cfrac{1}{2} \\ \\ 0 &\cfrac{\sqrt{3}}{2} &-\cfrac{\sqrt{3}}{2} \\ \\ \cfrac{\sqrt{2}}{2} &\cfrac{\sqrt{2}}{2} &\cfrac{\sqrt{2}}{2} \end{bmatrix} T3S/2S=N∗⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1022−212322−21−2322⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
注意: N N N为系数,做等幅值变换和等功率变换 N N N系数不同;
等幅值变换 N = 2 3 N =\cfrac{2}{3} N=32
等功率变换 N = 2 3 N =\sqrt\cfrac{2}{3} N=32
下面均为等幅值变换
3.1 Clarke变换
三相电流 A B C ABC ABC分别为 i A i_{A} iA, i B i_{B} iB, i C i_{C} iC,根据基尔霍夫电流定律满足以下公式:
i A + i B + i C = 0 i_{A}+i_{B}+i_{C} = 0 iA+iB+iC=0
静止坐标系 α β \alpha\beta αβ, α \alpha α轴的电流分量为 i α i_{\alpha} iα, i β i_{\beta} iβ,则Clark变换满足以下公式:
i α = i A i β = 1 3 ∗ i A + 2 3 ∗ i B i_{\alpha} = i_{A} \\ \\ i_{\beta} = \cfrac{1}{\sqrt{3}}*i_{A}+\cfrac{2}{\sqrt{3}}*i_{B} iα=iAiβ=31∗iA+32∗iB
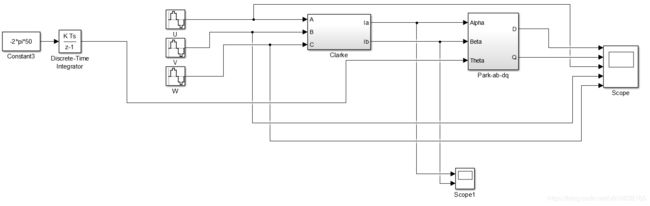
在matlab的simulink仿真如下图所示;
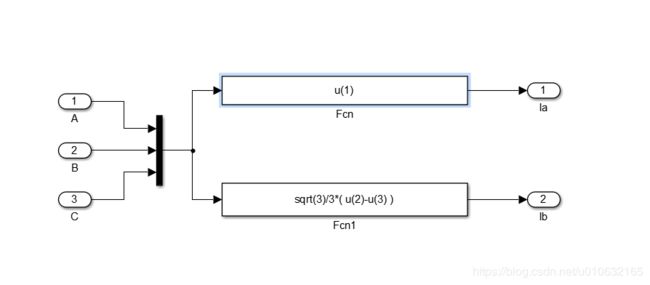
最终得到三相电流 i A i_{A} iA, i B i_{B} iB, i C i_{C} iC的仿真结果如下;
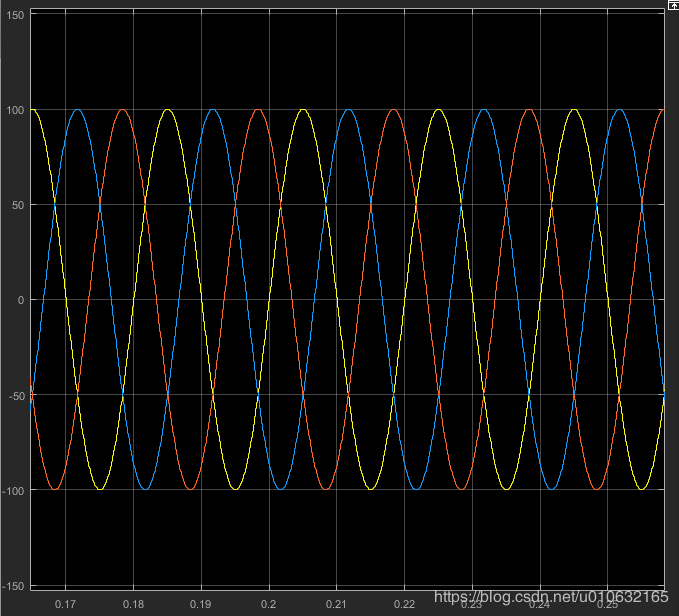
得到 α β \alpha\beta αβ 坐标的 i α i_{\alpha} iα 和 i β i_{\beta} iβ 的仿真结果如下图所示;
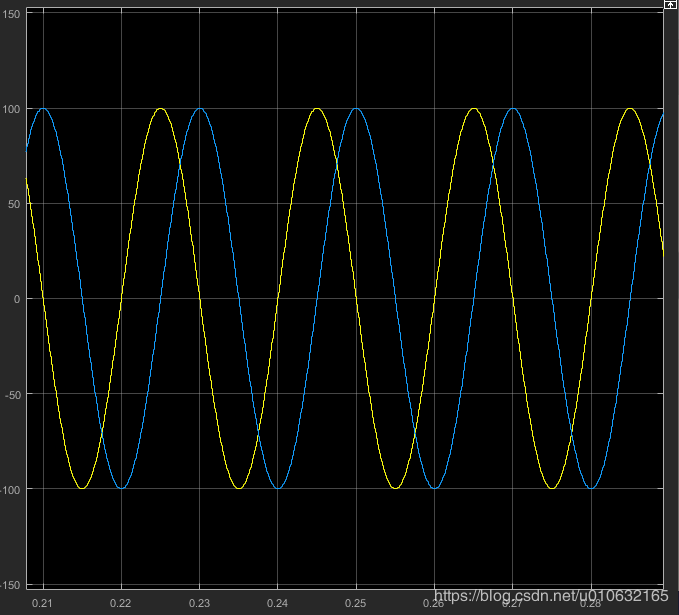
由上述两张图分析可以得到,等幅值Clark变换前后峰值不变, α β \alpha\beta αβ坐标系中 i α i_{\alpha} iα和 i β i_{\beta} iβ相位相差90°。
3.2 Clarke反变换
暂略
4 d q dq dq 坐标系
d q dq dq 坐标系相对与定子来说是旋转的坐标系,转速的角速度和转子旋转的角速度相同,所以,相当于转子来说, d q dq dq 坐标系就是静止的坐标系;而 i d i_{d} id和 i q i_{q} iq则是恒定不变的两个值,具体如下图所示;
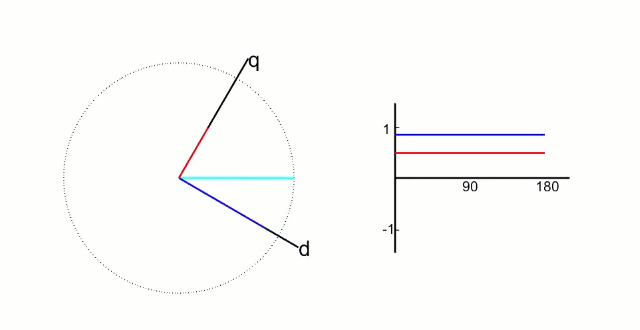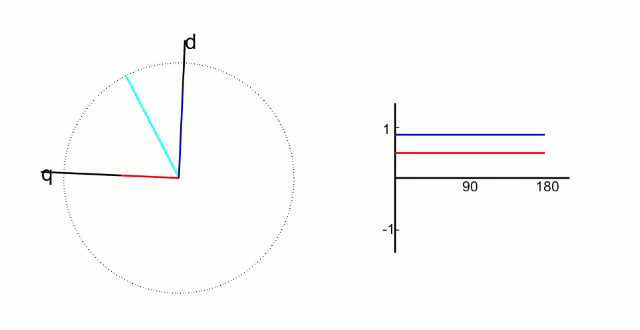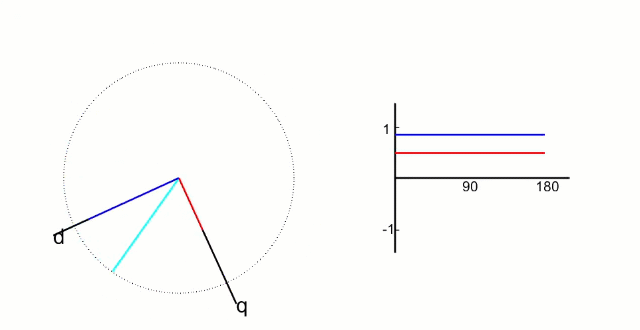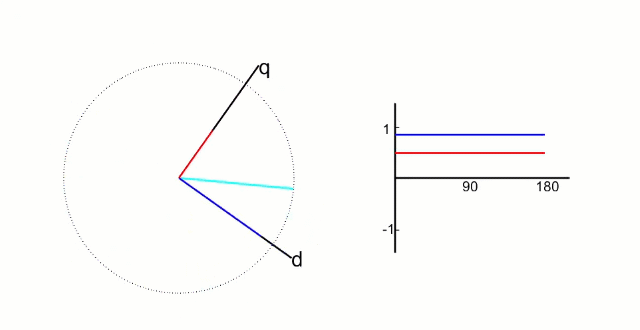
根据物理结构,我们发现;
d d d 轴方向与转子磁链方向重合,又叫直轴;
q q q 轴方向与转子磁链方向垂直,又叫交轴;
d d d轴和 q 轴 q轴 q轴如下图所示;
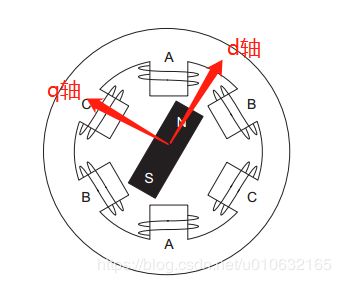
4.1 Park变换
Park变换的本质是静止坐标系 α β \alpha\beta αβ乘以一个旋转矩阵,从而得到 d q dq dq坐标系,其中满足以下条件:
[ f d f q ] = T 2 s / 2 r ∗ [ f α f β ] \begin{bmatrix} f_{d} \\ f_{q} \end{bmatrix} = T_{2s/2r}*\begin{bmatrix} f_{\alpha} \\ f_{\beta} \end{bmatrix} [fdfq]=T2s/2r∗[fαfβ]
其中 T 2 s / 2 r T_{2s/2r} T2s/2r为旋转矩阵,所以,park变换和park反变换其根本就是旋转矩阵不同, T 2 s / 2 r T_{2s/2r} T2s/2r可以表示为:
T 2 s / 2 r = [ c o s θ e s i n θ e − s i n θ e c o s θ e ] T_{2s/2r} = \begin{bmatrix} cos\theta_{e} & sin\theta_{e} \\ -sin\theta_{e} & cos\theta_{e} \end{bmatrix} T2s/2r=[cosθe−sinθesinθecosθe]
T 2 s / 2 r T_{2s/2r} T2s/2r 含义为 2 ∗ s t a t o r 2*stator 2∗stator ==> 2 ∗ r o t o r 2*rotor 2∗rotor
2轴定子坐标系转换到2轴转子坐标系
由上式可以得到:
{ i d = i α ∗ c o s θ + i β ∗ s i n θ i q = − i α ∗ s i n θ + i β ∗ c o s θ \begin{cases}i_{d}=i_{\alpha}*cos\theta+i_{\beta}*sin\theta \\ i_{q}=-i_{\alpha}*sin\theta+i_{\beta}*cos\theta\end{cases} {id=iα∗cosθ+iβ∗sinθiq=−iα∗sinθ+iβ∗cosθ
其中simulink仿真如下图所示;
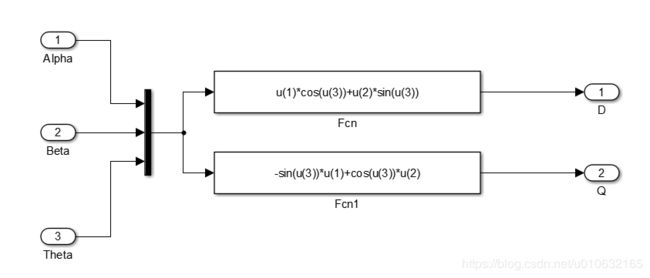
作为输入的 i α i_{\alpha} iα 和 i β i_{\beta} iβ,仿真波形如下图所示;

最终经过Park变换得到 i d i_{d} id和 i q i_{q} iq如下图所示;
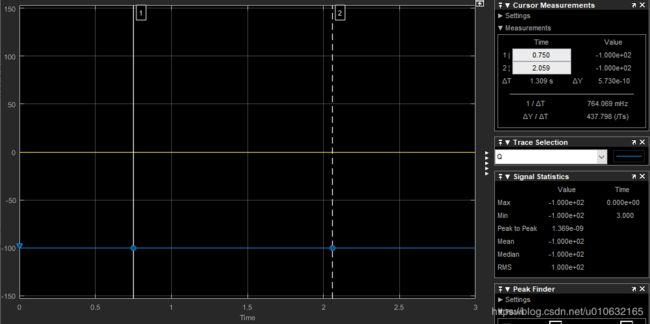
可以看到, i d i_{d} id和 i q i_{q} iq是恒定值,所以Park变换也叫做交直变换,由输入的交流量,最终变换到相对与转子坐标的直流量。
在实际写FOC的过程中对于这块变换产生了一个疑问;这里再区分一下正转和反转的情况,以此来说明一下Id和Iq的实际中的作用;
下面先规定一个方向为反转;
正转
通常,大部分书籍以及论文中的正转输入的三相波形如下:
{ U A = U m c o s θ e U B = U m c o s ( θ e − 2 π 3 ) U C = U m c o s ( θ e + 2 π 3 ) \begin{cases}U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \\ U_{C} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧UA=UmcosθeUB=Umcos(θe−32π)UC=Umcos(θe+32π)
反转
{ U A = U m c o s θ e U B = U m c o s ( θ e + 2 π 3 ) U C = U m c o s ( θ e − 2 π 3 ) \begin{cases}U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \\ U_{C} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \end{cases} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧UA=UmcosθeUB=Umcos(θe+32π)UC=Umcos(θe−32π)
4.2 Park反变换
Park反变换又叫直交变换,由 d q dq dq轴的直流量,最终变换到 α β \alpha\beta αβ的交流量,其中满足变换条件如下:
[ f d f q ] = T 2 r / 2 s ∗ [ f α f β ] \begin{bmatrix} f_{d} \\ f_{q} \\ \end{bmatrix} = T_{2r/2s}*\begin{bmatrix} f_{\alpha} \\ f_{\beta} \\ \end{bmatrix} [fdfq]=T2r/2s∗[fαfβ]
其中 T 2 s / 2 r T_{2s/2r} T2s/2r为Park变换的逆矩阵,所以,存在条件:
T 2 r / 2 s = T 2 r / 2 s − 1 = [ c o s θ e − s i n θ e s i n θ e c o s θ e ] T_{2r/2s} = T_{2r/2s}^{-1} = \begin{bmatrix} cos\theta_{e} & -sin\theta_{e} \\ sin\theta_{e} & cos\theta_{e} \\ \end{bmatrix} T2r/2s=T2r/2s−1=[cosθesinθe−sinθecosθe]
最终由上式可以得到:
{ i α = i d ∗ c o s θ − i q ∗ s i n θ i β = i d ∗ s i n θ + i q ∗ c o s θ \begin{cases}i_{\alpha}=i_{d}*cos\theta-i_{q}*sin\theta \\ i_{\beta}=i_{d}*sin\theta+i_{q}*cos\theta\end{cases} {iα=id∗cosθ−iq∗sinθiβ=id∗sinθ+iq∗cosθ
仿真暂略。
5 程序实现
坐标变换的C程序主要基于TI的IQMATH库进行实现,详情已经提交到附件。
如何使用这个库可以参考《STM32 使用IQmath实现SVPWM》
附件
链接:https://pan.baidu.com/s/1s2qU5wA2LMSmed51q-Jayw
提取码:irm2