轨迹规划 - 三次多项式and五次多项式
在轨迹规划中,有一个类别是多项式轨迹规划:抛物线、三次多项式、五次多项式、七次多项式、N次多项式。在这篇中,我们去掉最低,去掉最高,主要讲三次多项式和五次多项式这两种。
此处多项式轨迹规划中,建立的函数关系式是:关节转动的角度和时间之间的函数关系式。
三次多项式
函数关系式为:
![]()
两点之间,一段轨迹规划的起始时间是t0,结束时间是t1。
多项式中四个常量参数的计算公式为:
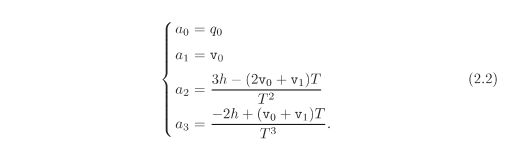
该公式中,q0是起始点关节角度,v0是起始点的关节角速度,T=t1-t0,h=q1-q0(q1是结束点的关节角度,q0是开始点的关节角度)
在使用以上公式进行轨迹规划时,有如下几个关键点:
- 起始和结束关节角度、速度、加速度已知。
- 需要对两点之间的轨迹进行插值,插值的方法,一般使用等时间间距的插值。
- 计算各个时间点的关节角度、关节速度、关节加速度。
- 关节角度的计算,使用三次多项式的函数关系式求解;关节速度,使用三次多项式的函数关系式的一次导数求解;关节加速度,使用三次多项式的函数关系式的二次导数求解。
针对两点之间的关节角度的三次多项式轨迹规划,使用matlab代码生成的关节角度、关节速度、关节加速度曲线如下所示:

此处,q0=0,q1=10;t0=0,t1=8;v0=v1=0
针对多点之间的关节角度的三次多项式轨迹规划,使用matlab代码生成的关节角度、关节速度、关节加速度曲线如下所示:

q0=10, q1=20, q2=0, q3=30, q4=40; t0=0, t1=2, t2=4, t3=8, t4=10; v0=0, v1=-10, v2=10, v3=3, v4=0
从以上曲线可以看出,三次多项式中,位移、速度是连续的,加速度是不连续的,具体参见加速度曲线中t=2,t=4,t=8处加速度的跳变。
五次多项式
函数关系式为:
![]()
两点之间,一段轨迹规划的起始时间是t0,结束时间是t1。
多项式中六个常量参数的计算公式为:

该公式中,q0是起始点关节角度,v0是起始点的关节角速度,v1是结束点的关节角速度,a0是起始点的关节角加速度,a1是结束点的关节角加速度,T=t1-t0,h=q1-q0(q1是结束点的关节角度,q0是开始点的关节角度)
在使用以上公式进行轨迹规划时,需要注意的点和三次多项式中的一样。
针对两点之间的关节角度的五次多项式轨迹规划,使用matlab代码生成的关节角度、关节速度、关节加速度曲线如下所示:

此处,q0=0,q1=10;t0=0,t1=8;v0=v1=0;a0=a1=0
针对多点之间的关节角度的五次多项式轨迹规划,使用matlab代码生成的关节角度、关节速度、关节加速度曲线如下所示:
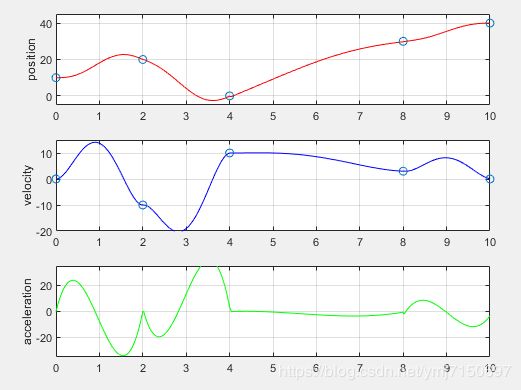
q0=10, q1=20, q2=0, q3=30, q4=40; t0=0, t1=2, t2=4, t3=8, t4=10; v0=0, v1=-10, v2=10, v3=3, v4=0; a0=a1=a2=a3=a4=0
从以上曲线可以看出,五次多项式中,位移、速度、加速度都是连续的。
另外,从三次多项式和五次多项式的曲线中,可以看出来,这两种轨迹规划的方式,整个过程中没有匀速阶段,一直处于加速或者是减速阶段。而在点胶等应用中,是需要机器人的运动过程一定有匀速阶段的。因此,此种应用的机器人,需要使用其他方式的轨迹规划方式。
