数据结构和算法(2)-栈与队列
引言
栈与队列两种实现方法:数组及链表。
数组实现采用“基于下标访问”( Index-based access)的模式,而链表实现则是基于“节点”( Node)或“位置”( Position)的概念。无论是哪种实现方式,栈与队列的每一基本操作都可以在常数时间内完成。
栈ADT
POP:移除栈定元素
| 操作 | 描述 |
|---|---|
| push(x) | 将对象 x 压至栈顶 |
| pop() | 若栈非空,则将栈顶对象移除,并将其返回否则,报错 |
| getSize() | 返回栈内当前对象的数目 |
| isEmpty() | 检查栈是否为空 |
| top() | 若栈非空,则返回栈顶对象(但并不移除)否则,报错 |
Stack接口
在 Java 的 java.util 包中已经专门为栈结构内建了一个类⎯⎯java.util.Stack。
任何 Java 对象都可以作为该内建类的栈元素,同时该类还提供了多种方法: push()、 pop()、 peek()
(功能等价于 top())、 getSize()以及 empty()(功能等价于 isEmpty())。在遇到空栈时,方法 pop()
和 peek()都会报意外错 ExceptionStackEmpty。
栈ADT的完整Java接口
Java抽象数据类型的实现过程,通常可以分为两步。
- 首先,要给出其应用程序接口定义( Application programming interface, API),简称接口( Interface)。接口的作用,就是明确ADT所支持方法的名称、声明及调用的形式。
- 此外,还要针对各种可能出现的错误条件,定义相应的意外。
栈ADT的完整Java接口:
public interface Stack {
public int getSize();//返回栈中元素数目
public boolean isEmpty();//判断栈是否为空
public Object top() throws ExceptionStackEmpty;//取栈顶元素(但不删除)
public void push (Object ele);//入栈
public Object pop() throws ExceptionStackEmpty;//出栈
}基于数组简单实现Stack接口
public class ExceptionStackEmpty extends RuntimeException {
public ExceptionStackEmpty(String err) {
super(err);
}
}ExceptionStackFull:这一例外并非栈ADT本身的要求,而只是针对数组实现而设置的
public class ExceptionStackFull extends RuntimeException {
public ExceptionStackFull(String err) {
super(err);
}
}
public class Stack_Array implements Stack {
public static final int CAPACITY = 1024;// 数组的默认容量
protected int capacity;// 数组的实际容量
protected Object[] S;// 对象数组
protected int top = -1;// 栈顶元素的位置
// 按默认容量创建栈对象
public Stack_Array() {
this(CAPACITY);
}
// 按指定容量创建栈对象
public Stack_Array(int cap) {
capacity = cap;
S = new Object[capacity];
}
// 获取栈当前的规模
public int getSize() {
return (top + 1);
}
// 测试栈是否为空
public boolean isEmpty() {
return (top < 0);
}
// 入栈
public void push(Object obj) throws ExceptionStackFull {
if (getSize() == capacity)
throw new ExceptionStackFull("意外:栈溢出");
S[++top] = obj;
}
// 取栈顶元素
public Object top() throws ExceptionStackEmpty {
if (isEmpty())
throw new ExceptionStackEmpty("意外:栈空");
return S[top];
}
// 出栈
public Object pop() throws ExceptionStackEmpty {
Object elem;
if (isEmpty())
throw new ExceptionStackEmpty("意外:栈空");
elem = S[top];
S[top--] = null;
return elem;
}
}正确性分析
在弹出栈顶之后,将原栈顶 S[top]置为 null 的操作似乎是多余(S[top--] = null;)的⎯⎯即使省略这一步,该方法依然符合 ADT 定义的要求。不过就 Java 语言而论,假设原栈顶为 e = S[top],在应用 pop()方法时将 S[top]置为 null,实际上就是告诉系统:该栈元素不再保留指向对象 e 的一个引用,将触发java内存垃圾回收.
容量和实际元素数要区分,只有发生元素变动,top值才会变更.
Stack-Array的时间复杂度分析:
| 操作方法 | 时间复杂度 |
|---|---|
| getSize() | O(1) |
| isEmpty() | O(1) |
| top() | O(1) |
| push() | O(1) |
| pop() | O(1) |
Stack-Array缺陷分析
内部数组的容量是事先固定,一些应用问题中,小容量的栈足以满足要求,此时固定的容量又会造成存储空间的浪费.
Java 虚拟机中的栈
看书.
队列ADT
特征:先进先出”( First-In-First-Out, FIFO)的原则;顾客们排成一个队列⎯⎯最先到达者优先得到服务;
PS:和栈相似,同样是放入(+1),移除(-1)
| 操作方法 | 功能描述 |
|---|---|
| enqueue(x) | 将元素 x 加到队列末端 |
| dequeue() | 若队列非空,则将队首元素移除,并将其返回否则,报错 |
| getSize() | 返回队列中当前包含的元素数目 |
| isEmpty() | 检查队列是否为空 |
| front() | 若队列非空,则返回队首元素(但并不移除)否则,报错 |
Queue 接口
public interface Queue {
public int getSize();//返回队列中元素数目
public boolean isEmpty();//判断队列是否为空
public Object front() throws ExceptionQueueEmpty;//取队首元素(但不删除)
public void enqueue (Object obj) throws ExceptionQueueFull;//入队
public Object dequeue() throws ExceptionQueueEmpty;//出队
public void Traversal();//遍历
}基于数组的实现
顺序数组:
仿照栈的实现,以 Q[0]作为队首,其它对象顺序往后存放。但每次首元素出队之后,都需要将后续的所有元素向前顺移一个单元⎯⎯若队长为 n,这项工作需要O(n)时间,因此效率很低
循环数组:
为了避免数组的整体移动,可以引入如下两个变量 f 和 r:
- f:始终等于 Q 的首元素在数组中的下标,即指向下次出队元素的位置
- r:始终等于 Q 的末元素的下标加一,即指向下次入队元素的位置
一开始, f = r = 0,此时队空。每次有对象入队时,将其存放于 Q[r],然后 r 加一,以指向下一单元。对称地,每次有对象出队之后,也将 f 加一,指向新的队首元素。这样,对 front()、 enqueue()和 dequeue()方法的每一次调用都只需常数时间。
按照上述约定,在队列的生命期内, f 和 r 始终在单调增加。因此,若队列数组的容量为 N,则在经过 N 次入队操作后, r 所指向的单元必然超出数组的范围;在经过 N 次出队操作后, f 所指向的单元也会出现类似的问题。
解决上述问题的一种简便方法,就是在每次 f 或 r 加一后,都要以数组的长度做取模运算,以保证其所指单元的合法性。就其效果而言,这就相当于把数组的头和尾相联,构成一个环状结构。
public class Queue_Array implements Queue {
public static final int CAPACITY = 1000;// 数组的默认容量
protected int capacity;// 数组的实际容量
protected Object[] Q;// 对象数组
protected int f = 0;// 队首元素的位置
protected int r = 0;// 队尾元素的位置
// 构造方法(空队列)
public Queue_Array() {
this(CAPACITY);
}
// 按指定容量创建对象
public Queue_Array(int cap) {
capacity = cap;
Q = new Object[capacity];
}
// 查询当前队列的规模
public int getSize() {
return (capacity - f + r) % capacity;
}
// 判断队列是否为空
public boolean isEmpty() {
return (f == r);
}
// 入队
public void enqueue(Object obj) throws ExceptionQueueFull {
if (getSize() == capacity - 1)
throw new ExceptionQueueFull("Queue overflow.");
Q[r] = obj;
r = (r + 1) % capacity;
}
// 出队
public Object dequeue() {
Object elem;
if (isEmpty())
throw new ExceptionQueueEmpty("意外:队列空");
elem = Q[f];
Q[f] = null;
f = (f + 1) % capacity;
return elem;
}
// 取(并不删除)队首元素
public Object front() throws ExceptionQueueEmpty {
if (isEmpty())
throw new ExceptionQueueEmpty("意外:队列空");
return Q[f];
}
// 遍历(不属于ADT)
public void Traversal() {
for (int i = f; i < r; i++)
System.out.print(Q[i] + " ");
System.out.println();
}
}数组实现,各方法的时间复杂度
| 操作方法 | 时间复杂度 |
|---|---|
| getSize() | O(1) |
| isEmpty() | O(1) |
| front() | O(1) |
| enqueue() | O(1) |
| dequeue() | O(1) |
队空与队满
当队列中不含任何对象时,必有 f = r。然而,反之却不然。
试考虑如下情况:在数组中只剩下一个空闲单元(此时有 f ≡ (r+1) mod N)时,需要插入一个
对象。若则按照上面的 enqueue()算法,插入后有 f = r(表示队列为空),但事实上此时的队列已满。如果根据“ f = r”
判断队列为空,则尽管队列中含有元素,但出队操作却无法进行;反过来,尽管数组空间已满,却还能插入新元素(原有的元素将被覆盖掉)。
为了解决这一问题,一种简便易行的方法就是禁止队列的实际规模超过N-1。
链表
栈与队列利用数组加以实现由于数组长度必须固定,在空间效率及适应性方面还存在不足.
单链表
链表( Linked list),就是按线性次序排列的一组数据节点;
每个节点都是一个对象,它通过一个引用element指向对应的数据元素,同时还通过一个引用next指向下一节点。
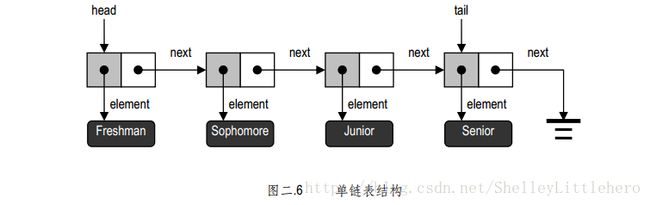
单链表节点类
element + next
/**
* @description 单链表节点类
*/
public class Node implements Position {
private Object element;// 数据对象
private Node next;// 指向后继节点
/**************************** 构造函数 ****************************/
public Node() {
this(null, null);
}// 指向数据对象、后继节点的引用都置空
public Node(Object e, Node n) {
element = e;
next = n;
}// 指定数据对象及后继节点
/**************************** Position接口方法 ****************************/
// 返回存放于该位置的元素
public Object getElem() {
return element;
}
// 将给定元素存放至该位置,返回此前存放的元素
public Object setElem(Object e) {
Object oldElem = element;
element = e;
return oldElem;
}
/**************************** 单链表节点方法 ****************************/
// 取当前节点的后继节点
public Node getNext() {
return next;
}
// 修改当前节点的后继节点
public void setNext(Node newNext) {
next = newNext;
}
}
单链表首末节点的插入与删除
单链表首节点的插入和删除可以在 O(1)时间完成;
假定我们借助一个引用tail始终指向的末节点,则在表尾插入新节点也只需O(1)时间;
而对于删除而言:
即使我们始终通过一个 tail 引用指向当前的末节点,末节点的删除操作也
不能在 O(1)时间内完成。其原因在于,只有在找到末节点的直接前驱节点之后,才能对表尾节点实
施删除操作。然而,为此我们不得不从链表的前端开始逐一检查各个节点—这需要 O(n)的时间。
基于单链表实现栈
这里设置了一个实例变量 top,指向表中的首节点。在新元素 e 入栈时,只需创建一个以 e 为数据的节点 v,并将 v 作为首节点插入。反过来,在退栈时,可以直接摘除首节点,并返回其数据。
这些操作都可以在 O(1)时间内完成,这一效率与基于数组的栈实现相同.
package chapter2;
public class Stack_List implements Stack {
protected Node top;// 指向栈顶元素
protected int size;// 栈中元素的数目
public Stack_List(Node top, int size) {
super();
this.top = null;
this.size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return (top == null) ? true : false;
}
// 读取(但不删除)栈顶
@Override
public Object top() throws ExceptionStackEmpty {
if (isEmpty())
throw new ExceptionStackEmpty("意外:栈空");
return top.getElem();
}
// 压栈,
@Override
public void push(Object ele) {
Node node = new Node(ele, top);
top = node;
size++;
}
//弹出栈顶
@Override
public Object pop() throws ExceptionStackEmpty {
if (isEmpty())
throw new ExceptionStackEmpty("意外:栈空");
Object elem = top.getElem();
top = top.getNext();
size--;
return elem;
}
}
基于单链表实现队列
package chapter2;
public class Queue_List implements Queue {
protected Node head;// 指向表首元素
protected Node tail;// 指向表末元素
protected int size;// 队列中元素的数目
public Queue_List(Node head, Node tail, int size) {
super();
this.head = null;
this.tail = null;
this.size = 0;
}
@Override
public int getSize() {
// TODO Auto-generated method stub
return size;
}
@Override
public boolean isEmpty() {
// TODO Auto-generated method stub
return 0 == size ? true : false;
}
//取(并不删除)队首元素
@Override
public Object front() throws ExceptionQueueEmpty {
if(isEmpty()) throw new ExceptionQueueEmpty("意外:队列空");
Object elem = head.getElem();
return elem;
}
// 入队(先进先出)
@Override
public void enqueue(Object obj) throws ExceptionQueueFull {
Node node = new Node();
node.setElem(obj);
node.setNext(null);
if (0 == size)
head = node;// 若此前队列为空,则直接插入
else
tail.setNext(node);// 否则,将新节点接至队列末端
tail = node;
size++;
}
// 出队
@Override
public Object dequeue() throws ExceptionQueueEmpty {
if (0 == size)
throw new ExceptionQueueEmpty("意外:队列空");
Object node = head.getElem();
head = head.getNext();
size--;
if (0 == size) tail = null;//若队列已空,须将末节点引用置空
return node;
}
@Override
public void Traversal() {
Node p = head;
while(null!=p){
System.out.println(p.getElem());
p= p.getNext();
}
}
}
位置Position
位置 ADT
| 操作方法 | 功能描述 |
|---|---|
| getElem(): | 返回存放于当前位置的元素 输入:无 输出:对象 |
| setElem(e): | 将元素 e 放入当前位置,并返回此处原先存放的元素 输入:一个元素 输出:一个元素 |
位置 ADT 接口
public interface Position {
public Object getElem();// 返回存放于该位置的元素
public Object setElem(Object e);// 将给定元素存放至该位置,返回此前存放的元素
}双端队列
双端队列的 ADT
双端队列ADT支持的基本操作:
| 操作方法 | 功能描述 |
|---|---|
| insertFirst(x): | 将对象 x 作为首元素插入 输入:一个对象 输出:无 |
| insertLast(x): | 将对象 x 作为末元素插入 输入:一个对象 输出:无 |
| removeFirst(): | 若队列非空,则将首元素删除,并将其内容返回 否则,报错 输入:无 输出:对象 |
| removeLast(): | 若队列非空,则将末元素删除,并将其内容返回否则,报错 输入:无 输出:对象 |
双端队列ADT支持的附加操作
| 操作方法 | 功能描述 |
|---|---|
| first(): | 若队列非空,则返回首元素的内容 否则,报错 输入:无 输出:对象 |
| last(): | 若队列非空,则返回末元素的内容 否则,报错 输入:无 输出:对象 |
双端队列的接口
public interface Deque {
public int getSize();// 返回队列中元素数目
public boolean isEmpty();// 判断队列是否为空
public Object first() throws ExceptionQueueEmpty;// 取首元素(但不删除)
public Object last() throws ExceptionQueueEmpty;// 取末元素(但不删除)
public void insertFirst(Object obj);// 将新元素作为首元素插入
public void insertLast(Object obj);// 将新元素作为末元素插入
public Object removeFirst() throws ExceptionQueueEmpty;// 删除首元素
public Object removeLast() throws ExceptionQueueEmpty;// 删除末元素
public void Traversal();// 遍历
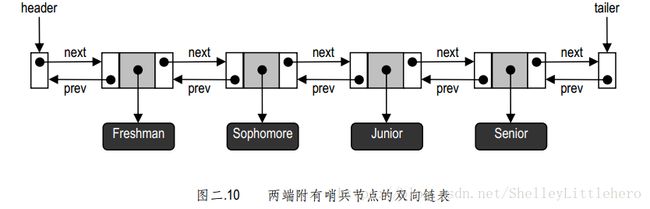
}双向链表节点类
这类链表中的每一节点不仅配有next引用,同时还
有一个prev引用,指向其直接前驱节点(没有前驱时为null)。
/**
* @description 基于位置接口实现的双向链表节点类
*/
public class DLNode implements Position {
private Object element;// 数据对象
private DLNode next;// 指向后继节点
private DLNode prev;// 指向前驱节点
public DLNode() {
this(null, null, null);
}
public DLNode(Object element, DLNode next, DLNode prev) {
super();
// 注意三个参数的次序:数据对象、前驱节点、后继节点
this.element = element;
this.next = next;
this.prev = prev;
}
/**************************** Position接口方法 ****************************/
@Override
public Object getElem() {
// TODO Auto-generated method stub
return element;
}
@Override
public Object setElem(Object e) {
Object oldElem = element;
element = e;
return oldElem;
}
/**************************** 双向链表节点方法 ****************************/
// 找到后继位置
public DLNode getNext() {
return next;
}
// 找到前驱位置
public DLNode getPrev() {
return prev;
}
// 修改后继位置
public void setNext(DLNode newNext) {
next = newNext;
}
// 修改前驱位置
public void setPrev(DLNode newPrev) {
prev = newPrev;
}
}基于双向链表实现的双端队列
头-首-中-末-尾
利用双向链表,可以使双端队列的每一方法都能在常数时间内完成。
package chapter2;
/**
* @description 基于双向链表实现双端队列结构
*/
public class Deque_DLNode implements Deque {
protected DLNode header;// 指向头节点(哨兵)
protected DLNode trailer;// 指向尾节点(哨兵)
protected int size;// 队列中元素的数目
// 构造函数
public Deque_DLNode() {
header = new DLNode();
trailer = new DLNode();
header.setNext(trailer);
trailer.setPrev(header);
size = 0;
}
// 返回队列中元素数目
public int getSize() {
return size;
}
// 判断队列是否为空
public boolean isEmpty() {
return (0 == size) ? true : false;
}
// 取首元素(但不删除)
public Object first() throws ExceptionQueueEmpty {
if (isEmpty())
throw new ExceptionQueueEmpty("意外:双端队列为空");
return header.getNext().getElem();
}
// 取末元素(但不删除)
public Object last() throws ExceptionQueueEmpty {
if (isEmpty())
throw new ExceptionQueueEmpty("意外:双端队列为空");
return trailer.getPrev().getElem();
}
// 在队列前端插入新节点
public void insertFirst(Object obj) {
DLNode second = header.getNext();
DLNode first = new DLNode(obj, header, second);
second.setPrev(first);
header.setNext(first);
size++;
}
// 在队列后端插入新节点
public void insertLast(Object obj) {
DLNode second = trailer.getPrev();
DLNode first = new DLNode(obj, second, trailer);
second.setNext(first);
trailer.setPrev(first);
size++;
}
// 删除首节点
public Object removeFirst() throws ExceptionQueueEmpty {
if (isEmpty())
throw new ExceptionQueueEmpty("意外:双端队列为空");
DLNode first = header.getNext();
DLNode second = first.getNext();
Object obj = first.getElem();
header.setNext(second);
second.setPrev(header);
size--;
return (obj);
}
// 删除末节点
public Object removeLast() throws ExceptionQueueEmpty {
if (isEmpty())
throw new ExceptionQueueEmpty("意外:双端队列为空");
DLNode first = trailer.getPrev();
DLNode second = first.getPrev();
Object obj = first.getElem();
trailer.setPrev(second);
second.setNext(trailer);
size--;
return (obj);
}
// 遍历
public void Traversal() {
DLNode p = header.getNext();
while (p != trailer) {
System.out.print(p.getElem() + " ");
p = p.getNext();
}
System.out.println();
}
}
转载自:Java数据结构,邓俊辉