manifold.LocallyLinearEmbedding(LLE)流形学习之局部线性嵌入算法详解
高维数据难于可视化,需先经过降维处理。
线性降维框架如Principal Component Analysis(PCA,主成分分析)、Independent Component Analysis(独立成分分析)、 Linear Discriminant Analysis(线性判别分析)等,但常会错失数据结构中的非线性项。
Manifold Learing可以看作一种生成类似PCA的线性框架,不同的是可以对数据中的非线性结构敏感。虽然存在监督变体,但是典型的流式学习问题是非监督的:它从数据本身学习高维结构,不需要使用既定的分类。
和传统的PCA,LDA等关注样本方差的降维方法相比,LLE关注于降维时保持样本局部的线性特征,由于LLE在降维时保持了样本的局部特征,它广泛的用于图像图像识别、高维数据可视化等领域。
-
流形学习
流形学习(Manifold Learning)是一大类基于流形的框架。
数学意义上的流形比较抽象,不过我们可以认为LLE中的流形是一个不闭合的曲面。这个流形曲面有数据分布比较均匀,且比较稠密的特征,有点像流水的味道。
基于流行的降维算法就是将流形从高维到低维的降维过程,在降维的过程中我们希望流形在高维的一些特征可以得到保留。
一个形象的流形降维过程如下图。我们有一块卷起来的布,我们希望将其展开到一个二维平面,我们希望展开后的布能够在局部保持布结构的特征,其实也就是将其展开的过程,就想两个人将其拉开一样。
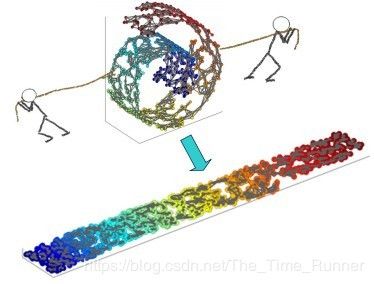
在局部保持布结构的特征,或者说数据特征的方法有很多种,不同的保持方法对应不同的流形算法。
比如等距映射(ISOMAP)算法在降维后希望保持样本之间的测地距离而不是欧式距离,因为测地距离更能反映样本之间在流形中的真实距离。
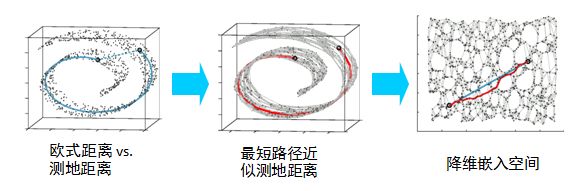
但是等距映射算法有一个问题就是他要找所有样本全局的最优解,当数据量很大,样本维度很高时,计算非常的耗时,鉴于这个问题,LLE通过放弃所有样本全局最优的降维,只是通过保证局部最优来降维。同时假设样本集在局部是满足线性关系的,进一步减少的降维的计算量。
-
LLE思想
-
历史
局部线性嵌入算法(Locally linear embedding, LLE)是一个非线性降维方法,由 Sam T.Roweis 和Lawrence K.Saul 于 2000 年提出并发表在《Science》杂志上。它能够使降维后的数据保持原有拓扑结构不变。现在已经广泛应用于图像数据的分类与聚类、文字识别、多维数据的可视化、以及生物信息学等领域中。
- 背景假设
LLE 是一种局部算法。它的主要思想是利用数据的局部线性来逼近全局线性:即假设任意样本点都可表示为其临近样本点的线性组合,在寻找数据的低维嵌入同时,保持这种邻域线性组合关系不变。
LLE首先假设数据在较小的局部是线性的,也就是说,某一个数据可以由它邻域中的几个样本来线性表示。
比如我们有一个样本x1,我们在它的原始高维邻域里用K-近邻思想找到和它最近的三个样本x2,x3,x4. 然后我们假设x1可以由x2,x3,x4线性表示,即: x 1 = w 12 x 2 + w 13 x 3 + w 14 x 4 x_1=w_{12}x_2+w_{13}x_3+w_{14}x_4 x1=w12x2+w13x3+w14x4
其中, w 12 , w 13 , w 14 w_{12},w_{13},w_{14} w12,w13,w14为权重系数。在我们通过LLE降维后,我们希望x1在低维空间对应的投影x1′和x2,x3,x4对应的投影*x2′,x3′,x4′*也尽量保持同样的线性关系,即 x 1 ≈ w 12 x 2 ′ + w 13 x 3 ′ + w 14 x 4 ′ x_1 \approx w_{12}x_2'+w_{13}x_3'+w_{14}x_4' x1≈w12x2′+w13x3′+w14x4′。
也就是说,投影前后线性关系的权重系数w12,w13,w14是尽量不变或者最小改变的。
从上面可以看出,线性关系只在样本的附近起作用,离样本远的样本对局部的线性关系没有影响,因此降维的复杂度降低了很多。
--------------------------------时代的分割线(一个非常有意思的现象)--------------------------
以上是用最传统的角度来描述LLE的背景假设,作者是个老派研究人员,下面这种写法,明显是新时代的研究者。思维不同,效率差别甚大,不得感慨,年轻人掌握的工具高效又有年轻的精力。
----------------------------------------时代的分割线-------------------------------------------
算法假定平滑流形在局部具有线性性质,一个点可以通过其局部领域内的点重构出来。先将下式(1)最小化:
ε ( W ) = ∑ i ∣ X i → − ∑ j W i j X j → ∣ 2 \varepsilon(W)=\sum_i|\overrightarrow{X_i} - \sum _jW_{ij} \overrightarrow {X_j}|^2 ε(W)=i∑∣Xi−j∑WijXj∣2
以求解出最有的局部线性重构矩阵 W W W,对于距离较远的点 i i i和 j j j, W i j W_{ij} Wij应当为零。这之后再将 W W W当作已知量对式(2)进行最小化。
Φ ( Y ) = ∑ i ∣ Y → i − ∑ j W i j Y → j ∣ 2 \Phi(Y) = \sum_i|\overrightarrow Y_i - \sum_jW_{ij} \overrightarrow Y_j|^2 Φ(Y)=i∑∣Yi−j∑WijYj∣2
这里 Y Y Y成了变量,也就是降维后的向量,对这个式子求最小化的意义就是要求如果原来的数据 X i X_i Xi可以以 W W W矩阵里对应的稀疏根据其邻域内的点重构出来的话,那么降维过后的数据也应该保持这个性质(具体参考)。
-
LLE算法步骤
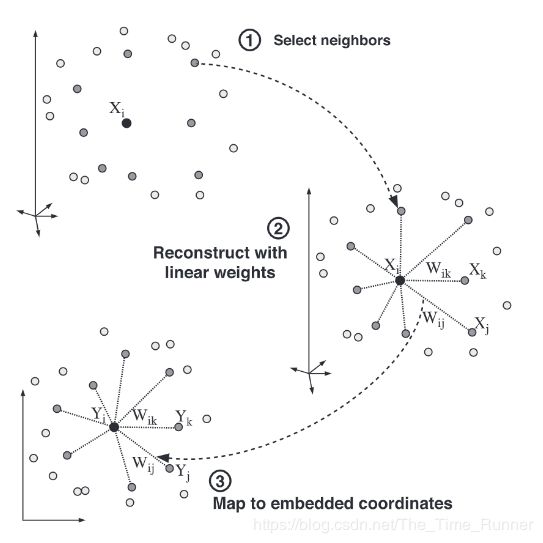
LLE算法可以归纳为三步:
- 寻找每个样本点的k个近邻点
- 由每个样本点的近邻点计算出该样本点的局部重建权制矩阵 W W W
- 由该样本点的局部重建权制矩阵 W W W和其近邻点计算出该样本点的输出值
如图所示:
-
sklearn.manifold.LocallyLinearEmbedding(局部线性嵌入) 官方文档
-
Reference
- ArrowLuo
- 局部线性嵌入(LLE)原理总结
- Roweis, S. & Saul, L. Nonlinear dimensionality reduction by locally linear embedding. Science 290:2323 (2000).