Transformer

Transformer
利用self-attention和position embedding克服了RNN中的长距离依赖、无法并行计算的缺点，也解决了CNN中远距离特征捕获难的问题。

encoder
encoder由6层相同的层组成，每一层分别由两部分组成：
第一部分： multi-head self-attention mechanism
第二部分：position-wise feed-forward network 是一个全连接层两个部分都有一个残差连接（residual connection）接一个layer normalization。

decoder
decoder由6个相同的层组成，每一层包括以下3个部分：
第一部分： multi-head self-attention mechanism
第二部分： multi-head context-attention mechanism
第三部分： position-wise feed-forward network每一个部分都有一个残差连接，后接一个layer normalization。

Scaled dot-product attention
论文中的描述：通过确定Q和K之间的相似程度来选择V！

为什么要加缩放因子呢？
当dk很大时，点积得到的结果维度很大，使得结果处于softmax函数梯度很小的区域。梯度很小的情况，对于反向传播不利。

K,Q,V是什么？
* 在encoder的self-attention中， Q、K、V都来自同一个地方（相等），他们是上一层encoder的输出。对于第一层encoder，它们就是word embedding和positional encoding相加得到的输入。
* 在decoder的self-attention中，Q、K、V都来自于同一个地方（相等），它们是上一层decoder的输出。对于第一层decoder，它们就是word embedding和positional encoding相加得到的输入。但是对于decoder，我们不希望它能获得下一个time step（即将来的信息）因此我们需要进行sequence masking。
* 在encoder-decoder attention中，Q来自于decoder的上一层的输出，K和V来自于encoder的输出，K和V是一样的。

其中mask：scores.masked_fill(mask = 0, -1e9)，用于把mask是0的变成一个很小的数，这样后面经过softmax之后的概率就很接近零(但是理论上还是用来很少一点点未来的信息)。

Multi-head attention
理解了Scaled dot-product attention，Multi-head attention也很简单了。论文提到，他们发现将Q、K、V通过一个线性映射之后，分成 h份，对每一份进行scaled dot-product attention效果更好。然后，把各个部分的结果合并起来，再次经过线性映射，得到最终的输出。这就是所谓的multi-head attention。上面的超参数h就是heads数量。论文默认是8。上面说的分成h份是在dk,dq,dv维度上面进行切分的。因此，进入到scaled dot-profuct attention的dk实际上等于未进入之前的D_model/h。（512/8）

context-attention
它是encoder和decoder之间的attention！所以，你也可以称之为encoder-decoder attention!

Residual connection
假设网络中某个层对输入x作用后的输出是F(x），那么增加residual connection之后，就变成了：F(x)+x。这个+x操作就是一个shortcut。残差结构的好处：因为增加了一项x，那么该层网络对x求偏导的时候，多了一个常数项1，所以在反向传播过程中，梯度连乘，也不会造成梯度消失。

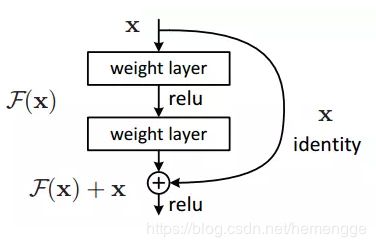
layer normalization
Normalization有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为0方差为1的数据。我们在把数据送入激活函数之前进行normalization（归一化），因为我们不希望输入数据落在激活函数的饱和区。Batch Normalization (BN)的主要思想就是：在每一层的每一批数据上进行归一化。我们可能会对输入数据进行归一化，但是经过该网络层的作用后，我们的的数据已经不再是归一化的了。随着这种情况的发展，数据的偏差越来越大，我的反向传播需要考虑到这些大的偏差，这就迫使我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。

MASK
Transformer模型里面涉及两种mask。分别是padding mask和sequence mask。 其中，padding mask在所有的scaled dot-product attention里面都需要用到，而sequence mask只有在decoder的self-attention里面用到。
什么是padding mask呢？回想一下，我们的每个批次输入序列长度是不一样的！也就是说，我们要对输入序列进行对齐！具体来说，就是给在较短的序列后面填充0。因为这些填充的位置，其实是没什么意义的，所以我们的attention机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。 具体的做法是，把这些位置的值加上一个非常大的负数(可以是负无穷)，这样的话，经过softmax，这些位置的概率就会接近0！ 而我们的padding mask实际上是一个张量，每个值都是一个Boolen，值为fasle的地方就是我们要进行处理的地方。
sequence mask是为了使得decoder不能看见未来的信息。也就是对于一个序列，在time_step为t的时刻，我们的解码输出应该只能依赖于t时刻之前的输出，而不能依赖t之后的输出。因此我们需要想一个办法，把t之后的信息给隐藏起来。 那么具体怎么做呢？也很简单：产生一个上三角矩阵，上三角的值全为1，下三角的值权威0，对角线也是0。把这个矩阵作用在每一个序列上，就可以达到我们的目的啦。
Decoder和Encoder有一个关键的不同：Decoder在解码第t个时刻的时候只能使用1…t时刻的输入，而不能使用t+1时刻及其之后的输入。因此我们需要一个函数来产生一个Mask矩阵，代码如下：

def subsequent_mask(size):
    "Mask out subsequent positions."
    attn_shape = (1, size, size)
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(subsequent_mask) = 0

它的输出：
print(subsequent_mask(5))

输出 1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
我们发现它输出的是一个方阵，对角线和下面都是1。第一行只有第一列是1，它的意思是时刻1只能attend to输入1，第三行说明时刻3可以attend to {1,2,3}而不能attend to{4,5}的输入，因为在真正Decoder的时候这是属于Future的信息。知道了这个函数的用途之后，上面的代码就很容易理解了。代码首先使用triu产生一个上三角阵：
0 1 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
0 0 0 0 0
然后需要把0变成1，把1变成0，这可以使用 matrix == 0来实现。

positional encoding
就目前而言，我们的Transformer架构似乎少了点什么东西。没错，就是它对序列的顺序没有约束！我们知道序列的顺序是一个很重要的信息，如果缺失了这个信息，可能我们的结果就是：所有词语都对了，但是无法组成有意义的语句！为了解决这个问题。论文提出了Positional encoding。这是啥？一句话概括就是：对序列中的词语出现的位置进行编码！如果对位置进行编码，那么我们的模型就可以捕捉顺序信息！那么具体怎么做呢？论文的实现很有意思，使用正余弦函数。公式如下：

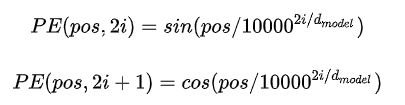
其中，pos是指词语在序列中的位置，可以看出，在偶数位置，使用正弦编码，在奇数位置使用余弦编码。这个编码公式的意思就是：给定词语的位置pos，我们可以把它编码成d_model维的向量！也就是说，位置编码的每一个维度对应正弦曲线，波长构成了从2pai到10000*2pai的等比序列。上面的位置编码是绝对位置编码。但是词语的相对位置也非常重要。这就是论文为什么要使用三角函数的原因！正弦函数能够表达相对位置信息。，主要数学依据是以下两个公式：

上述公式说明，对于词汇之间的位置偏移k，PE(pos+k)可以表示成PE（pos）和PE(k)的组合形式，这就是表达相对位置的能力。