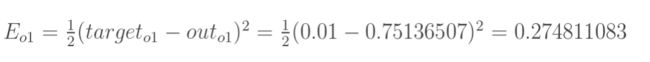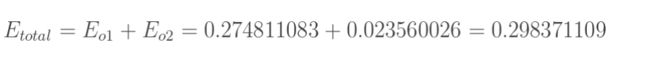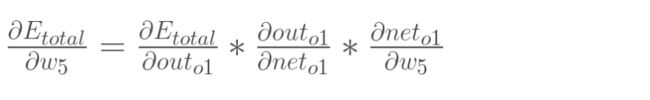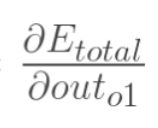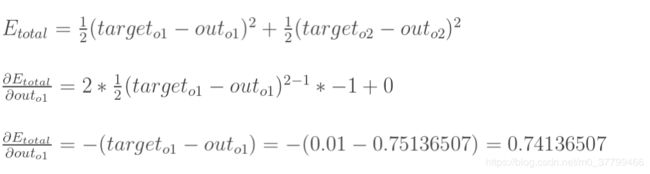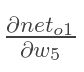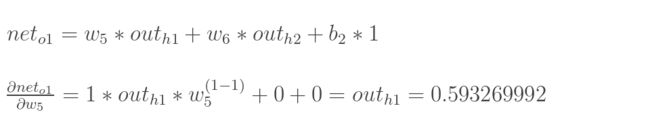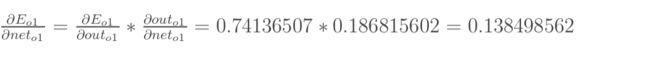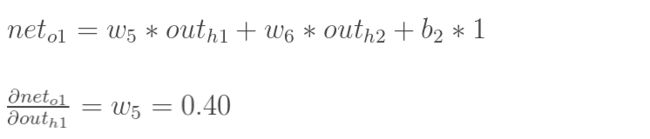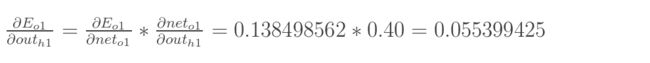神经网络的前向和反向传播

1、前向传播

前向传播的作用就是为了获取误差损失；现在以示例来说明：

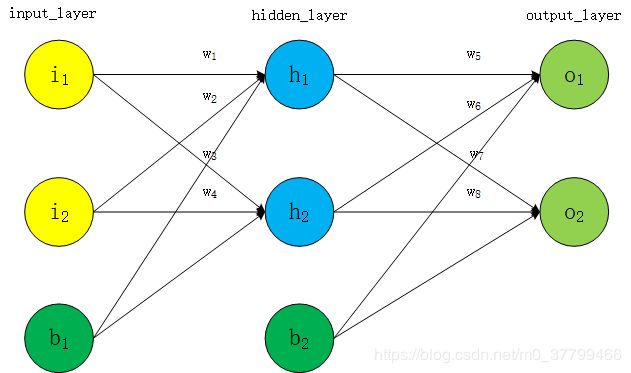
上图是一个典型的神经网络结构，包括了输入层、隐含层和输出层，为了更好的讲解，现在对其进行赋值：

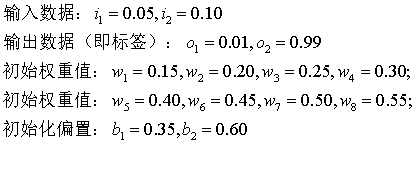
目标：给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。

（1）.输入层---->隐含层：

计算神经元h1的输入加权和：

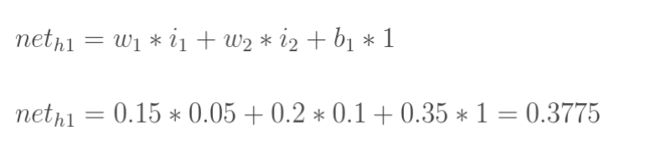
　　神经元h1的输出:(此处用到激活函数为sigmoid函数)：
　　
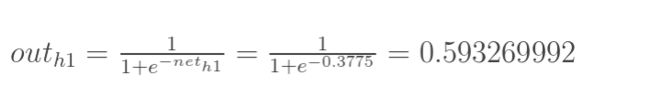
　　同理，可计算出神经元h2的输出：
　　
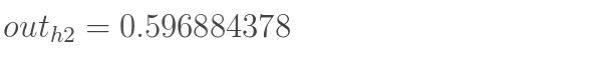
　　（2）.隐含层---->输出层：

同样的方法计算输出层神经元o1和o2的值：
　　
　　
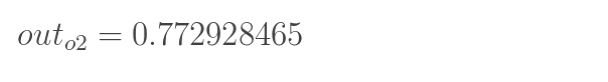
　　这样前向传播的过程就结束了，我们得到输出值为 [0.75136079 , 0.772928465]，与实际值
　　[0.01 , 0.99] 相差还很远，现在我们对误差进行反向传播，更新权值，重新计算输出。

2、反向传播

反向传播的作用就是为了将误差传给每层，然后根据误差调整权重参数；
（1）.计算总误差
总误差：(square error)

但是有两个输出，所以分别计算o1和o2的误差，总误差为两者之和：

（2）.隐含层---->输出层的权值更新：

以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）

下面的图可以更直观的看清楚误差是怎样反向传播的：

现在我们来分别计算每个式子的值：

计算：

计算：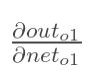

（这一步实际上就是对sigmoid函数求导，比较简单，可以自己推导一下）

计算：

最后三者相乘：

这样我们就计算出整体误差E(total)对w5的偏导值。
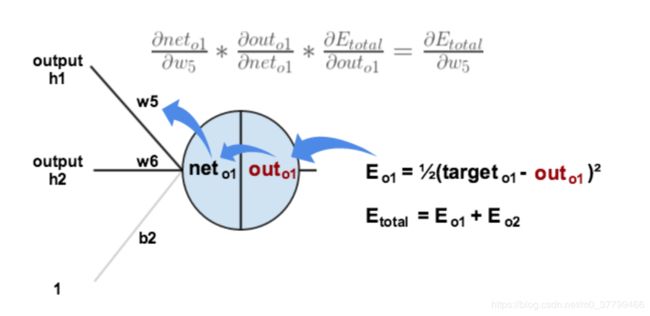
回过头来再看看上面的公式，我们发现：

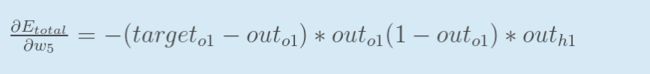
为了表达方便，用来表示输出层的误差：

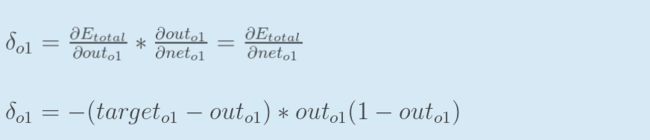
因此，整体误差E(total)对w5的偏导公式可以写成：

如果输出层误差计为负的话，也可以写成：

最后我们来更新w5的值：

（其中，是学习速率，这里我们取0.5）

同理，可更新w6,w7,w8:

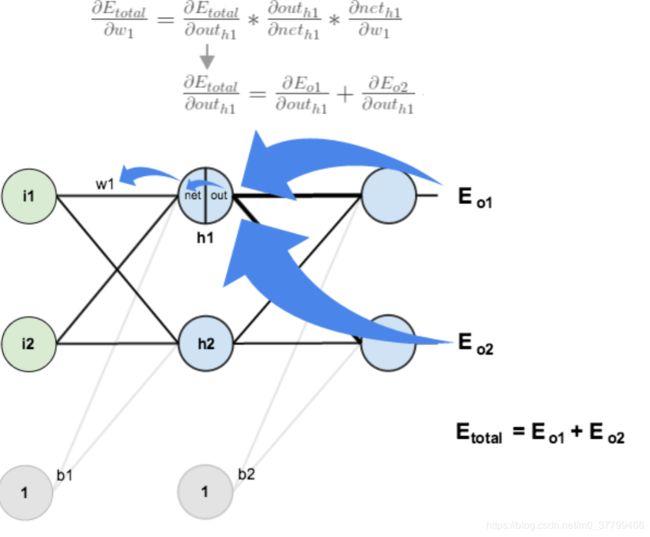
（3）.隐含层---->输入层的权值更新：

方法其实与上面说的差不多，但是有个地方需要变一下，在上文计算总误差对w5的偏导时，是从out(o1)---->net(o1)---->w5,此时out(o1)的计算只有E(total)中的E(o1)这一支参与了；但是在隐含层之间的权值更新时，是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差，所以这个地方两个都要计算。
　
　计算：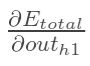

先计算：



这里的w5还是没有更新的权重；

同理，计算出：

　　　　　　　　　　
两者相加得到总值：

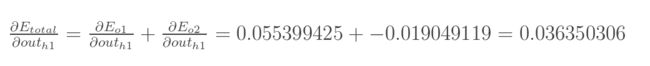
再计算：

再计算：

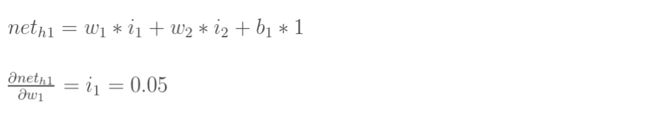
最后，三者相乘：

为了简化公式，用**sigma(h1)**表示隐含层单元h1的误差：

最后，更新w1的权值：

同理，额可更新w2,w3,w4的权值：

　　这样误差反向传播法就完成了，最后我们再把更新的权值重新计算，不停地迭代，在这个例子中第一次迭代之后，总误差E(total)由0.298371109下降至0.291027924。迭代10000次后，总误差为0.000035085，输出为0.015912196,0.984065734,证明效果还是不错的。
　　代码(Python):

#coding:utf-8
import random
import math

#
#   参数解释：
#   "pd_" ：偏导的前缀
#   "d_" ：导数的前缀
#   "w_ho" ：隐含层到输出层的权重系数索引
#   "w_ih" ：输入层到隐含层的权重系数的索引

class NeuralNetwork:
    LEARNING_RATE = 0.5

    def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None):
        self.num_inputs = num_inputs

        self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)
        self.output_layer = NeuronLayer(num_outputs, output_layer_bias)

        self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
        self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)

    def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):
        weight_num = 0
        for h in range(len(self.hidden_layer.neurons)):
            for i in range(self.num_inputs):
                if not hidden_layer_weights:
                    self.hidden_layer.neurons[h].weights.append(random.random())
                else:
                    self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
                weight_num += 1

    def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):
        weight_num = 0
        for o in range(len(self.output_layer.neurons)):
            for h in range(len(self.hidden_layer.neurons)):
                if not output_layer_weights:
                    self.output_layer.neurons[o].weights.append(random.random())
                else:
                    self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
                weight_num += 1

    def inspect(self):
        print('------')
        print('* Inputs: {}'.format(self.num_inputs))
        print('------')
        print('Hidden Layer')
        self.hidden_layer.inspect()
        print('------')
        print('* Output Layer')
        self.output_layer.inspect()
        print('------')

    def feed_forward(self, inputs):
        hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)
        return self.output_layer.feed_forward(hidden_layer_outputs)

    def train(self, training_inputs, training_outputs):
        self.feed_forward(training_inputs)

        # 1. 输出神经元的值
        pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)
        for o in range(len(self.output_layer.neurons)):

            # ∂E/∂zⱼ
            pd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])

        # 2. 隐含层神经元的值
        pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)
        for h in range(len(self.hidden_layer.neurons)):

            # dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼ
            d_error_wrt_hidden_neuron_output = 0
            for o in range(len(self.output_layer.neurons)):
                d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]

            # ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂
            pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()

        # 3. 更新输出层权重系数
        for o in range(len(self.output_layer.neurons)):
            for w_ho in range(len(self.output_layer.neurons[o].weights)):

                # ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼ
                pd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)

                # Δw = α * ∂Eⱼ/∂wᵢ
                self.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight

        # 4. 更新隐含层的权重系数
        for h in range(len(self.hidden_layer.neurons)):
            for w_ih in range(len(self.hidden_layer.neurons[h].weights)):

                # ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢ
                pd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)

                # Δw = α * ∂Eⱼ/∂wᵢ
                self.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weight

    def calculate_total_error(self, training_sets):
        total_error = 0
        for t in range(len(training_sets)):
            training_inputs, training_outputs = training_sets[t]
            self.feed_forward(training_inputs)
            for o in range(len(training_outputs)):
                total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])
        return total_error

class NeuronLayer:
    def __init__(self, num_neurons, bias):

        # 同一层的神经元共享一个截距项b
        self.bias = bias if bias else random.random()

        self.neurons = []
        for i in range(num_neurons):
            self.neurons.append(Neuron(self.bias))

    def inspect(self):
        print('Neurons:', len(self.neurons))
        for n in range(len(self.neurons)):
            print(' Neuron', n)
            for w in range(len(self.neurons[n].weights)):
                print('  Weight:', self.neurons[n].weights[w])
            print('  Bias:', self.bias)

    def feed_forward(self, inputs):
        outputs = []
        for neuron in self.neurons:
            outputs.append(neuron.calculate_output(inputs))
        return outputs

    def get_outputs(self):
        outputs = []
        for neuron in self.neurons:
            outputs.append(neuron.output)
        return outputs

class Neuron:
    def __init__(self, bias):
        self.bias = bias
        self.weights = []

    def calculate_output(self, inputs):
        self.inputs = inputs
        self.output = self.squash(self.calculate_total_net_input())
        return self.output

    def calculate_total_net_input(self):
        total = 0
        for i in range(len(self.inputs)):
            total += self.inputs[i] * self.weights[i]
        return total + self.bias

    # 激活函数sigmoid
    def squash(self, total_net_input):
        return 1 / (1 + math.exp(-total_net_input))


    def calculate_pd_error_wrt_total_net_input(self, target_output):
        return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();

    # 每一个神经元的误差是由平方差公式计算的
    def calculate_error(self, target_output):
        return 0.5 * (target_output - self.output) ** 2


    def calculate_pd_error_wrt_output(self, target_output):
        return -(target_output - self.output)


    def calculate_pd_total_net_input_wrt_input(self):
        return self.output * (1 - self.output)


    def calculate_pd_total_net_input_wrt_weight(self, index):
        return self.inputs[index]


# 文中的例子:

nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6)
for i in range(10000):
    nn.train([0.05, 0.1], [0.01, 0.09])
    print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))


#另外一个例子，可以把上面的例子注释掉再运行一下:

# training_sets = [
#     [[0, 0], [0]],
#     [[0, 1], [1]],
#     [[1, 0], [1]],
#     [[1, 1], [0]]
# ]

# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
# for i in range(10000):
#     training_inputs, training_outputs = random.choice(training_sets)
#     nn.train(training_inputs, training_outputs)
#     print(i, nn.calculate_total_error(training_sets))