机器学习(十)分类算法之朴素贝叶斯(Naive Bayes)算法
贝叶斯定理
首先我们来了解一下贝叶斯定理:
贝叶斯定理是用来做什么的?简单说,概率预测:某个条件下,一件事发生的概率是多大?
了解一下公式
事件B发生的条件下,事件A发生的概率为:
这里写图片描述
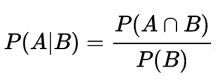
同理可得,事件A发生的条件下,事件B发生的概率为:

很容易推导得到:
![]()
假设若P(A)≠0,那么就可以得到用来预测概率的贝叶斯定理了:

这个定理显然是可以推导到多个条件的,比如在2个条件的情况下: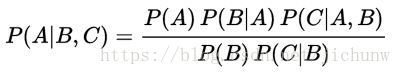
朴素贝叶斯定义:
我们之所以称之为朴素,是因为我们做了一个简单的假设,即类中特定特征的存在与任何其他特征的存在无关,这意味着每个特征彼此独立。
通过以上定理和“朴素”的假定,我们知道:
P( Category | Document) = P ( Document | Category ) * P( Category) / P(Document)


经典案例
-
信某宗教的人是恐怖分子的概率是多少?
假设 100% 的恐怖分子都相信某宗教,而某人相信某宗教,并不代表此人 100% 是恐怖分子,还需要考虑先验概率,假设全球有 7万 恐怖分子(全球人口 70亿 ),假设全球有 1/3 的人口相信某宗教,那么这个人是恐怖分子的概率是多少?
解:
我们要求解的是这个概率: P(恐怖分子|信某教)
套用公式,得到 :P(恐怖分子|信某教) = P(信某教|恐怖分子) P(恐怖分子) / P(信某教) = 100% * (7万人/70亿人) / (1/3) = 0.003%也即十万分之三的概率。
延展开去,从数学理论上讲,民主党不针对某个信教人群是对的,但是题目中设定 100% 的恐怖分子信某教,这个假设就比较… -
检测呈阳性的雇员吸毒概率是多少?
假设一个常规的检测结果的敏感度与可靠度均为 99% ,即吸毒者每次检测呈阳性 (+) 的概率为 99% 。而不吸毒者每次检测呈阴性 (-) 的概率为 99% 。假设某公司对全体雇员进行吸毒检测,已知 0.5% 的雇员吸毒。请问每位检测结果呈阳性的雇员吸毒的概率有多高?
解:
我们要求解的是这个概率: P(吸毒|检测呈阳性的雇员)
套用公式,得到 :P(吸毒|检测呈阳性雇员) = P(检测呈阳性雇员|吸毒) P(吸毒) / P(检测呈阳性雇员) = 99% * 0.5% / [P(检测呈阳性雇员∩吸毒) + P(检测呈阳性∩不吸毒)] = 99% * 0.5% / [P(检测呈阳性雇员|吸毒) * P(吸毒) + P(检测呈阳性|不吸毒) * P(不吸毒)] = 99% * 0.5% / [99% * 0.5% + 1% * 99.5%] = 0.3322也就是说,尽管吸毒检测的准确率高达 99% ,但贝叶斯定理告诉我们:如果某人检测呈阳性,其吸毒的概率只有大约 33% ,不吸毒的可能性比较大。
不过也要注意,检测的准确率高低,十分影响结果的概率,如果检测精度达到 99.9% ,那么检测呈阳性的雇员吸毒的概率就上升到了 83.39% 。 -
垃圾邮件的过滤
这是 Paul Graham 在 《黑客与画家》 中提到的办法。这个问题其实可以倒推,我们要求解的是这个概率: P(垃圾邮件|检测到某种特征) 。
这个某种特征可以是 关键词,可以是 时间,可以是 频次,可以是 邮件附件类型 …包括以上各种特征 混合 的特征等等。
我们先用最简单的 关键词 来做推测,根据我个人的经验,一个中国式垃圾邮件很可能会包含两个字:发票 。好,那么我们要求解的一封邮件是不是垃圾邮件的概率就变成 P(垃圾邮件|检测到“发票”关键词),根据贝叶斯定理P(垃圾邮件|检测到“发票”关键词) = P(检测到“发票”关键词|垃圾邮件) / P(检测到“发票”关键词)好,这里遇到了一个问题,我们怎么知道垃圾邮件里出现 发票 关键词的概率?
怎么知道在所有邮件里出现 发票 关键词的概率?理论上,除非我们统计所有邮件,否则我们是得不出的。这时候,就得做个妥协,在工程上做个近似,我们自己找到一定数量的真实邮件,并分为两组,一组正常邮件,一组垃圾邮件,然后进行计算,看 发票 这个词,在垃圾邮件中出现的概率是多少,在正常邮件里出现的概率是多少。
显然,这里的训练数量大一些的话,计算得到的概率会更逼近真实值。 Paul Graham 使用的邮件规模,是正常邮件和垃圾邮件各 4000封 。如果某个词只出现在垃圾邮件中, Paul Graham 就假定,它在正常邮件的出现频率是 1% ,反之亦然,这样做是为了避免概率为 0 。随着邮件数量的增加,计算结果会自动调整。
这样的话,将公式继续分解为如下:P(垃圾邮件|检测到“发票”关键词) = P(检测到“发票”关键词|垃圾邮件) / P(检测到“发票”关键词) = P(检测到“发票”关键词|垃圾邮件) / [P(检测到“发票”关键词∩垃圾邮件) + P(检测到“发票”关键词∩正常邮件)] = P(检测到“发票”关键词|垃圾邮件) / [P(检测到“发票”关键词|垃圾邮件) / P(垃圾邮件) + P(检测到“发票”关键词|正常邮件) / P(正常邮件)]就又可以根据训练模型得到的概率,进行初始值计算了。此后,可以通过大量用户将垃圾邮件标注为正常邮件,正常邮件挪到垃圾邮件的动作,进行反复训练纠正,直至逼近一个合理值了。
不过这里还涉及到一个问题,就是单个关键词的概率(单个条件)无论如何再高,这封邮件仍然有可能不是垃圾邮件,所以在此处应用贝叶斯定理时,我们显然要用到多个条件,也就是计算这个概率:
P(垃圾邮件|检测到“A”关键词,检测到“B”关键词,检测到"C",…)
Paul Graham 的做法是,选出邮件中 P(垃圾邮件|检测到“X”关键词) 最高的 15个词 ,计算它们的联合概率。(如果关键词是第一次出现,Paul Graham 就假定这个值等于 0.4 ,也即认为是negative normal)。
朴素贝叶斯分类方法
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法 。最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model,NBM)
和决策树模型相比,朴素贝叶斯分类器(Naive Bayes Classifier,或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。
验证每一个类别中,样本特征的分布情况;根据新样本中特征的分布情况预测属于每一个类别的概率,输出概率最大的类别,我们就认为该样本属于这个类别
案例:
假设有一个数据集,由两类组成(简化问题),对于每个样本的分类,我们都已经知晓。数据分布如下图(图取自MLiA):
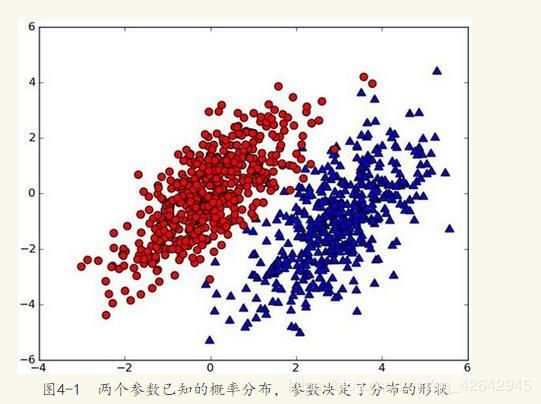
现在出现一个新的点new_point (x,y),其分类未知。我们可以用p1(x,y)表示数据点(x,y)属于红色一类的概率,同时也可以用p2(x,y)表示数据点(x,y)属于蓝色一类的概率。那要把new_point归在红、蓝哪一类呢?
我们提出这样的规则:
如果p1(x,y) > p2(x,y),则(x,y)为红色一类。
如果p1(x,y)
换人类的语言来描述这一规则:选择概率高的一类作为新点的分类。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
用条件概率的方式定义这一贝叶斯分类准则:
如果p(red|x,y) > p(blue|x,y), 则(x,y)属于红色一类。
如果p(red|x,y) < p(blue|x,y), 则(x,y)属于蓝色一类。
也就是说,在出现一个需要分类的新点时,我们只需要计算这个点的
max(p(c1 | x,y),p(c2 | x,y),p(c3 | x,y)…p(cn| x,y))。其对于的最大概率标签,就是这个新点的分类啦。
那么问题来了,对于分类i 如何求解p(ci| x,y)?
没错,就是贝叶斯公式:

概率基础
概率(Probability)定义
- 概率定义为一件事情发生的可能性
- 扔出一个硬币,结果头像朝上
- P(X) : 取值在[0, 1]
女神是否喜欢计算案例
在讲这两个概率之前我们通过一个例子,来计算一些结果:


计算结果为:
P(喜欢) = 4/7
P(程序员, 匀称) = 1/7
P(程序员|喜欢) = 2/4 = 1/2
P(程序员, 超重|喜欢) = 1/4
思考题:在小明是产品经理并且体重超重的情况下,如何计算小明被女神喜欢的概率?
即P(喜欢|产品, 超重) = ?
联合概率、条件概率与相互独立
- 联合概率:包含多个条件,且所有条件同时成立的概率
- 记作:P(A,B)
- 条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率
- 记作:P(A|B)
- 相互独立:如果P(A, B) = P(A)P(B),则称事件A与事件B相互独立。

如果职业和体型是相互独立的,p(职业,体型)=p(职业)* p(体型)
贝叶斯公式
计算案例
那么思考题就可以套用贝叶斯公式这样来解决:
P(喜欢|产品, 超重) = P(产品, 超重|喜欢)P(喜欢)/P(产品, 超重)
上式中,P(产品, 超重|喜欢)和P(产品, 超重)的结果均为0,导致无法计算结果。这是因为我们的样本量太少了,不具有代表性,本来现实生活中,肯定是存在职业是产品经理并且体重超重的人的,P(产品, 超重)不可能为0;而且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独立的事件,但是,根据我们有限的7个样本计算“P(产品, 超重) = P(产品)P(超重)”不成立。
而朴素贝叶斯可以帮助我们解决这个问题。
朴素贝叶斯,简单理解,就是假定了特征与特征之间相互独立的贝叶斯公式。
也就是说,朴素贝叶斯,之所以朴素,就在于假定了特征与特征相互独立。
所以,思考题如果按照朴素贝叶斯的思路来解决,就可以是
P(产品, 超重) = P(产品) * P(超重) = 2/7 * 3/7 = 6/49
p(产品, 超重|喜欢) = P(产品|喜欢) * P(超重|喜欢) = 1/2 * 1/4 = 1/8
P(喜欢|产品, 超重) = P(产品, 超重|喜欢)P(喜欢)/P(产品, 超重) = 1/8 * 4/7 / 6/49 = 7/12
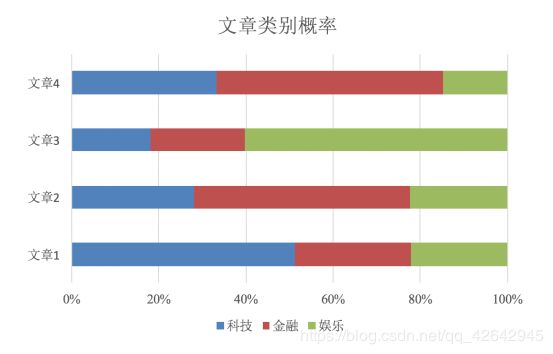
那么这个公式如果应用在文章分类的场景当中,我们可以这样看:
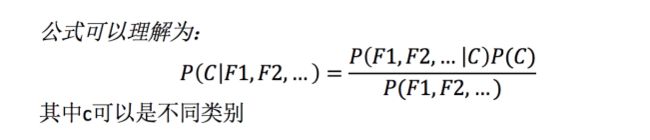
公式分为三个部分:
- P©:每个文档类别的概率(某文档类别数/总文档数量)
- P(W│C):给定类别下特征(被预测文档中出现的词)的概率
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- Ni为该F1词在C类别所有文档中出现的次数
- N为所属类别C下的文档所有词出现的次数和
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- P(F1,F2,…) 预测文档中每个词的概率
如果计算两个类别概率比较:所以我们只要比较前面的大小就可以,得出谁的概率大
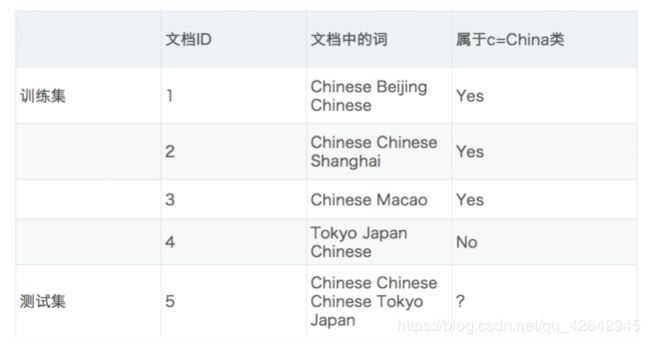
文章分类计算
- 计算结果
P(C|Chinese, Chinese, Chinese, Tokyo, Japan) --> P(Chinese, Chinese, Chinese, Tokyo, Japan|C) * P(C) = P(Chinese|C)^3 * P(Tokyo|C) * P(Japan|C) * P(C)
P(Chinese|C) = 5/8
P(Tokyo|C) = 0
P(Japan|C) = 0
API
在scikit-learn中,一共有3个朴素贝叶斯的分类算法类。分别是GaussianNB,MultinomialNB和BernoulliNB。其中GaussianNB就是先验为高斯分布的朴素贝叶斯,MultinomialNB就是先验为多项式分布的朴素贝叶斯,而BernoulliNB就是先验为伯努利分布的朴素贝叶斯。
这里我们使用MultinomialNB就是先验为多项式分布的朴素贝叶斯
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
案例:20类新闻分类
步骤分析
- 进行数据集的分割
- TFIDF进行的特征抽取
- 将文章字符串进行单词抽取
- 朴素贝叶斯预测
代码
- 进行数据集的分割
import sklearn.datasets
from sklearn.model_selection import train_test_split #数据集切分
from sklearn.feature_extraction.text import TfidfVectorizer #文本转换器
from sklearn.naive_bayes import MultinomialNB #朴素贝叶斯算法
# 获取新闻的数据,20个类别
news = sklearn.datasets.fetch_20newsgroups(data_home=None,subset='train')
# 进行数据集分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.3)
- TFIDF进行的特征抽取
- 将文章字符串进行单词抽取
# 对于文本数据,进行特征抽取
tf = TfidfVectorizer()
x_train = tf.fit_transform(x_train)
# 这里打印出来的列表是:训练集当中的所有不同词的组成的一个列表
print(tf.get_feature_names())
# 不能调用fit_transform
x_test = tf.transform(x_test)
- 朴素贝叶斯预测
# estimator估计器流程
mlb = MultinomialNB(alpha=1.0)
mlb.fit(x_train, y_train)
# 进行预测
y_predict = mlb.predict(x_test)
print("预测每篇文章的类别:", y_predict[:100])
print("真实类别为:", y_test[:100])
print("预测准确率为:", mlb.score(x_test, y_test))
朴素贝叶斯算法总结
- 优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
- 缺点:
- 由于使用了样本属性独立性的假设,所以如果特征属性有关联时其效果不好