NSGAII（带精英策略的非支配排序的遗传算法）

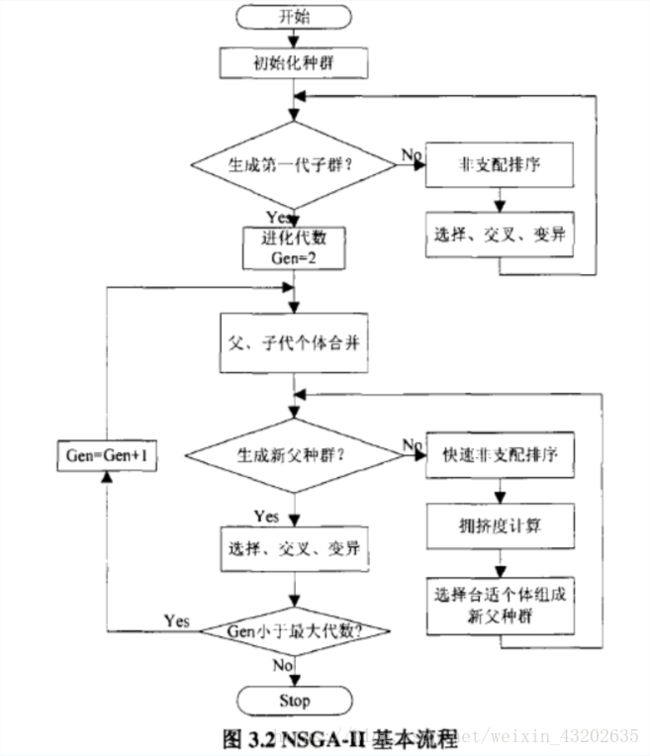
NSGA一II算法的基本思想：

（1）首先,随机产生规模为N的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群;
（2）其次,从第二代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;
（3）最后,通过遗传算法的基本操作产生新的子代种群:依此类推,直到满足程序结束的条件。

---

1. 快速的非支配排序

该算法需要保存两个量：
(1).支配个数np。该量是在可行解空间中可以支配个体p的所有个体的数量。
(2).被支配个体集合SP。该量是可行解空间中所有被个体p支配的个体组成的集合。
排序算法的伪代码如下：

def fast_nondominated_sort( P ):
    F = [ ]
    for p in P:
        Sp = [ ]
         np = 0
         for q in P:
             if p > q:                #如果p支配q，把q添加到Sp列表中
                 Sp.append( q )
             else if p < q:        #如果p被q支配，则把np加1
                 np += 1

        if np == 0:
            p_rank = 1        #如果该个体的np为0，则该个体为Pareto第一级
      F1.append( p )
    F.append( F1 )
    i = 0
    while F[i]:
        Q = [ ]
        for p in F[i]:
            for q in Sp:        #对所有在Sp集合中的个体进行排序
                nq -= 1
                if nq == 0:     #如果该个体的支配个数为0，则该个体是非支配个体
                    q_rank = i+2    #该个体Pareto级别为当前最高级别加1。此时i初始值为0，所以要加2
                    Q.append( q )
        F.append( Q )
        i += 1

2.排挤算法和精英策略

原始的NSGA算法中使用共享函数的方法来维持物种的多样性，这种方法包含一个**共享参数，该参数为所求解问题中所期望的共享范围。在该范围内，两个个体共享彼此的适应度。**但是该方法有两个难点：
(1).共享函数方法在保持多样性的性能很大程度上依赖于所选择的共享参数值。
(2).种群中的每个个体都要与其余的个体相比较，因此该方法的全局复杂度为O(N2)。

在NSGA2中使用了排挤算法和精英策略来代替共享函数算法。而要实现这两种方法，首先我们需要定义两个操作：密度估算和排挤算子。

(1).密度估算
要对拥挤距离进行计算，则需要根据每个目标函数对种群中的所有个体按升序进行排序。第一个和最后一个个体的拥挤距离设为无穷大，第i个个体的拥挤距离则设为第i+1和第i个体的所有目标函数值之差的和。具体方法如下面伪代码：

f crowding_distance_assignment( I )
        nLen = len( I )        #I中的个体数量
    for i in I:
                i.distance = 0    #初始化所有个体的拥挤距离
    for objFun in M:        #M为所有目标函数的列表
                I = sort( I, objFun )    #按照目标函数objFun进行升序排序
                I[0] = I[ len[I]-1 ] = ∞    #对第一个和最后一个个体的距离设为无穷大
                for i in xrange( 1, len(I) - 2 ):
                        I[i].distance = I[i].distance + ( objFun( I[i+1] ) - objFun( I[i-1] ) )/(Max(objFun()) - Min(objFun()) )

伪代码中的objFun( i )是对个体i求其目标函数值。Max(objFun())为目标函数objFun()的最大值，Min(objFun())为目标函数objFun的最小值。其复杂度为O(MNlogN)。

3.主体循环部分

(1).随机初始化开始种群P0。并对P0进行非支配排序，初始化每个个体的rank值。
(2). t = 0
(3).通过二进制锦标赛法从Pt选择个体，并进行交叉和变异重点内容操作，产生新一代种群Qt。
(4) 计算新种群的obj值，
(5).通过合并Pt 和 Qt 产生出组合种群Rt = Pt UQt 。
(6).对Rt进行非支配排序，并通过排挤和精英保留策略选出N个个体，组成新一代种群Pt+1。
(7).跳转到步骤3，并循环，直至满足结束条件。
步骤5的具体操作可见下图：
伪代码如下：

while condition:
    Rt = Pt + Qt
    F = fast_nondominate_sort( Rt )   //快速非支配排序
    Pt+1 = [ ]
    i = 0
    while len(Pt+1) + len( F[i] ) < N:
        crowding_distance_assignment( F[i] )   //密度估算
        Pt+1 += F[i]
        i += 1
    Pt+1 += F[i][0:N-len(Pt+1)]
    Qt+1 = make_new_generation( Pt+1 )
    t = t+1

二进制锦标赛法：

锦标赛法是选择操作的一种方法。
假设种群规模为n，该法的步骤为：

1.随机产生n个个体作为第一代（其实这步准确的说不是属于选择操作的，但每个算子并没有绝对的界限，这个是在选择操作之前的必做之事）；
2.从这n个个体中随机（注意是随机）选择k（k小于n）个个体，k的取值小，效率就高（节省运行时间），但不宜太小，一般取为n/2（取整）；
3.从这k个个体中选择最大的一个个体（涉及到排序的方法），作为下一代n个个体中的一个个体
4.重复2-4步，至得到新的n个个体；
5.进行这新的n个个体之间的交叉操作。