《数据库系统概念》学习笔记——第六章 形式化关系查询语言
Table of Contents
第六章 形式化关系查询语言
6.1 关系代数
6.1.1 基本运算
6.1.2 关系代数的形式化定义
6.1.3 附加的关系代数运算
6.1.4 扩展的关系代数运算
6.2 元组关系推演
6.2.1 查询示例
6.2.2 形式化定义
6.2.3 表达式的安全性
6.2.4 语言的表达能力
6.3 域关系运算
6.3.1 形式化定义
6.3.2 查询的例子
6.3.3 表达式的安全性
6.3.4 语言的表达能力
总结
第六章 形式化关系查询语言
6.1 关系代数
关系代数是一种过程化查询语言,它包括一个运算的集合,这些关系以一个或两个关系为输人,产生一个新的关系作为结果。
- 基本运算:选择、投影、更名、并、集合差、笛卡尔积
- 其他运算:集合交、自然连接、赋值、外连接、广义投影、聚集运算
6.1.1 基本运算
- 一元运算:选择、投影、更名
- 二元运算:并、集合差、笛卡尔积
基本运算能够增强关系代数的表达能力。
6.1.1.1 选择运算 (select)
选择(select)运算选出满足给定谓词的元组。
例如:下面的公式代表从instructor关系中选出dept_name=”Physics“的元组
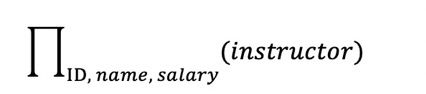 |
允许在选择谓词中间进行比较:=,≠,>,≥, <, ≤
选择谓词之间也可以使用连词:and(⋀), or(⋁), not(¬)将多个谓词合并为一个较大的谓词
6.1.1.2 投影运算
投影(project)运算使得我们可以选出想要的属性,把另一些属性排除在外。
例如:选择出instructor的ID,name和salary列
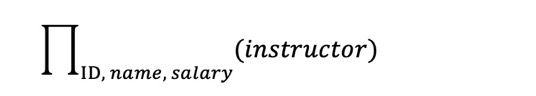 |
6.1.1.3 关系运算的组合
注意:关系运算的结果本身也是 一个关系。
把多个关系代数运算可以组成一个关系代数表达式(relational-algebra expression)。
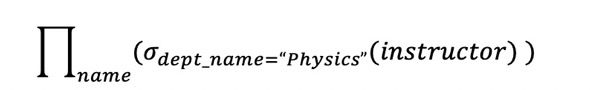 |
6.1.1.4 并运算
并(union)运算将两个集合取并集。
要使得并运算(r ∪ s)有意义,需要同时满足下面两个条件:
- r和s是同元的,即它们的属性数目必须相同
- 对所有的i, r的第i个属性的域必须与s的第i个属性的域相同
例如:下面的公式要找出在2009年秋季或2010年春季开设的课程的集合
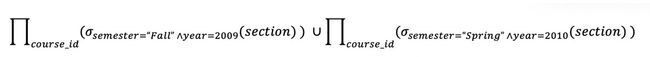 |
6.1.1.5 集合差运算
集合差(set-difference)运算能够找出在一个关系中而不在另一个关系中的那些元组。用r-s表示在r中而不在s中的元组。
与并运算一样,有意义的集合差运算也需要同时满足两个条件,确保其相容。
例如:找出所有开设在2009年秋季,但是在2010年春季不开设的课程
 |
6.1.1.6 笛卡尔积运算
笛卡尔积(cartesian-product)运算,用乘号(×)表示。
关系r1有n1个元组,关系r2有n2个元组,则r1×r2共有n1×n2个元组。
例子:找出物理系的老师,以及他们所教授的课程
instructor(ID, name, dept_name, salary)
teaches(ID,course_id, sec_id,semesters)
 |
注意:关系代数表达式不是唯一的,上述两个式子是等价的(equivalent)
6.1.1.7 更名运算
更名(rename)运算可以重命名关系。用ρ表示。
下面的式子表示把名字x赋予E。
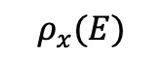 |
假设E是n元的,下面的式子表示把名字x赋予E,并将它的属性更名为A1, A2, ..., An。
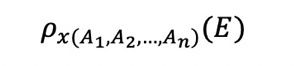 |
例如:找出大学里面的最高工资
- 步骤1:计算出由非最高工资组成的临时关系
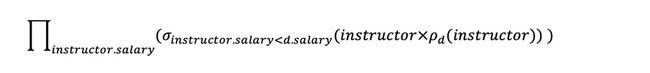 |
- 步骤2:instructor中的salary与刚刚计算出的临时关系的集合差
 |
更名运算不是必须的,也可以使用位置标记。可以使用位置标记隐含的作为关系的属性名。
用$1,$2,...指代第一个属性,第二个属性.....
例如:下面的关系表达式等价于上面的步骤2的表达式,$4代表第一个关系的salary属性,$8代表第二个关系的salary
 |
6.1.2 关系代数的形式化定义
关系代数的基本表达式必须是如下二者之一:
- 数据库中的一个关系
- 常数关系。例如:{(2222,Einstein, Physics, 95000),(2223,Emma, English, 96000) }
下列这些都是关系代数表达式:
- 并、交集、差集、投影、选择、更名
6.1.3 附加的关系代数运算
6.1.3.1 集合交运算
集合的交(Intersection)运算。
例如:找出2009年秋季和2010年春季都开课的课程。
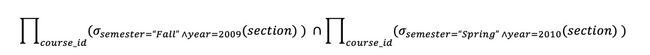 |
r∩s=r-(r-s)===>因此,集合交不是基本运算,不能增强关系代数的表达能力。
6.1.3.2 自然连接运算
自然连接(join)用符号⋈表示,例如:
 |
自然连接运算首先形成两个关系的笛卡尔积,再在两个关系中都出现的属性上的相等值进行选择,最后去除重复性。
自然连接的形式化定义。设r(R)和s(S)是两个关系,R和S分别是关系r和关系s所包含的属性列表。r和s的自然连接可表示为r⋈s,
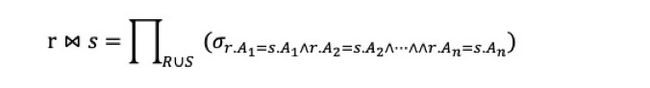 |
其中
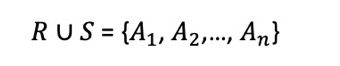 |
注意:自然连接满足可结合的(associative) :(a⋈b)⋈c=a⋈(b⋈c)
theta连接(theta join)是自然连接的扩展,它可以把一个选择运算和一个笛卡尔积运算合并为单独的一个运算。若r(R)和s(S)两个关系,θ是R∪S的属性上的谓词,则theta连接运行可定义为:
 |
6.1.3.3 赋值运算
赋值(assignment)运算用←表示。
例如:temp1 ← R×S 将右侧的结果赋值给左侧的关系变量
6.1.3.4 外连接运算
外连接运算(outer join)是连接运算的扩展,可以处理缺失的信息。
外连接有三种:左外连接、右外连接、全外链接
6.1.4 扩展的关系代数运算
6.1.4.1 广义投影运算
广义投影(generalized-projection):通过运行在投影列表中使用算术运算和字符串函数等来对投影进行扩展,定义如下:
6.1.4.2 聚集运算
聚集函数(aggregate function)输入值的一个汇总,将单一值作为结果返回。包括:
- sum、average、count、min、max、count_distinct
举例:
多重集(multiset):允许一个值出现多次的集合称为多重集。
多重集(multiset relational algrebra)运算:对多重集进行操作。
6.2 元组关系推演
用{t|P(t)}表示,所有事谓词P为真的元组t的集合。
6.2.1 查询示例
找出所有工资为80000美元以上的教师的ID,name, dept_name和salary:
{t|t∈instructor ∧ t[salary]>80000}
存在结构:表示关系r中存在元组t使得谓词Q(t)为真
或(∨), 与(∧),非(¬)
蕴含(⟹) :P⟹Q表示如果P为真,则Q为真。逻辑上等价于¬PVQ
存在,全部
6.2.2 形式化定义
元组关系演算表达式具有如下形式:{t|P(t)}
其中P是一个公式。公式中可以出现多个元组变量。
变量分为 自由变量和 受限变量。不被∃或∀修饰的变量称为自由变量。
元组关系演算的公式由原子构成。原子可以是如下形式之一:
6.2.3 表达式的安全性
元组关系演算表达式可能产生一个无线的关系。例如:
不在instructor中的元组有无限多个,大多数这样的元组所包含的数值甚至都不在数据库中!这是我们不希望看到的。
域(domain), dom(P)表示元祖关系公式P所引用的所有值的集合。它既包括P中显示出现的值,及名称出现在P中的那些关系所涉及到的关系的元组中出现的所有值。
dom(t∈instructor ∧ t[salary]>5000)是包括所有工资大于5000的instructor元组的集合。
上图中的关系表示是不安全的,因为dom(图中表达式)是所有出现在instructor中的值的集合,但是事实上t可能不在instructor中,包含不在instructor中出现的内容。
如果出现在表达式{t|P(t)}结果中的所有值均来自domain(P), 则{t|P(t)}是安全的。
6.2.4 语言的表达能力
断言:对于每个只运用基本操作(笛卡尔积,选择,投影,并,集合差)的关系代数表达式<==>都有与之等价的元组关系表达水;反之亦然。
6.3 域关系运算
域关系演算(domain relational calculus): 使用从属性域中取值的域变量,而不是整个元组的进行关系演算。
6.3.1 形式化定义
6.3.2 查询的例子
6.3.3 表达式的安全性
6.3.4 语言的表达能力
当我们把域关系运算限制在安全表达式范围内,它与被限制在安全表达式范围内的元组关系表达式具有相同的表达能力。
下述三者是等价的:
- 基本关系代数(不包括扩展关系代数运算)
- 限制在安全表达式范围内的元组关系演算
- 限制在安全表达式范围内的域关系运算
总结
- 关系代数(relational algebra)定义了一套在表上运算且输出结果也是表的代数运算。这些运算可以混合使用来得到表达式所希望查询的表达式。关系代数定义了关系查询语言中使用的基本运算。
- 关系代数运算可分为:
- 基本运算,包括:选择、投影、并、差、笛卡尔积、更名
- 附加的运算,可以用基本运算表达,包括:交、自然连接、赋值、外连接
- 扩展的运算,其中的一些扩展了关系代数的表达能力,包括:广义投影、聚集
- 关系代数是一种简洁的、形式化的语言,不适用于那些偶尔使用数据库系统的用户。因此,商用数据库系统采用更多”语法修饰“的语言。SQL是基于关系代数的
- 元组关系演算(tuple relational calculus)和域关系演算(domain relational calculus)是非过程化语言,代表了关系查询语言所需的基本能力。基本关系代数是一种非过程化语言,在能力上等价于被限制在安全表达式范围内的关系演算的两种形式
- 关系演算是简洁的、形式化的语言,并不适合于那些偶尔使用数据库系统的用户。这两种形式化语言构成了两种更易使用的语言QBE和Datalog的基础。