用python进行简单有限元分析——二维4单元9节点总刚度组装以及9个节点的力和位移求解

2020年数值分析作业，已成功实现，可直接复制代码运行！！

1、大概的理论。这里主要讲总刚度矩阵的组装原理，如何得到单元刚度矩阵请看添加链接描述https://blog.csdn.net/Youngist/article/details/106651143

2、实现得到4单元9节点总刚度矩阵的源代码

from math import *
import numpy as np
from matplotlib import pyplot as plt



# 1个单元四个节点
def shapefunction(r,s):#形函数
    N1 = 1 / 4 * (1 - r) * (1 - s)
    N2 = 1 / 4 * (1 + r) * (1 - s)
    N3 = 1 / 4 * (1 + r) * (1 + s)
    N4 = 1 / 4 * (1 - r) * (1 + s)
    return N1,N2,N3,N4

def diffNdr(r,s): # 求dNidr
    dN1dr = 1 / 4 * (-1) * (1 - s)
    dN2dr = 1 / 4 * (1) * (1 - s)
    dN3dr = 1 / 4 * (1) * (1 + s)
    dN4dr = 1 / 4 * (-1) * (1 + s)
    dNdr = [dN1dr,dN2dr,dN3dr,dN4dr]
    return dNdr


def diffNds(r,s): # 求dNids
    dN1ds = 1 / 4 * (1 - r) * (-1)
    dN2ds = 1 / 4 * (1 + r) * (-1)
    dN3ds = 1 / 4 * (1 + r) * (1)
    dN4ds = 1 / 4 * (1 - r) * (1)
    dNds = [dN1ds, dN2ds, dN3ds, dN4ds]
    return dNds

def jacobian(x,y,r,s): # 求J,Jinv,Jdet
    dNdr = diffNdr(r,s)
    dNds = diffNds(r,s)

    dxdr = x[0]*dNdr[0]+x[1]*dNdr[1]+x[2]*dNdr[2]+x[3]*dNdr[3]
    dxds = x[0]*dNds[0]+x[1]*dNds[1]+x[2]*dNds[2]+x[3]*dNds[3]
    dydr = y[0]*dNdr[0]+y[1]*dNdr[1]+y[2]*dNdr[2]+y[3]*dNdr[3]
    dyds = y[0]*dNds[0]+y[1]*dNds[1]+y[2]*dNds[2]+y[3]*dNds[3]

    J = np.array([[dxdr,dxds],[dydr,dyds]])
    Jdet = np.linalg.det(J)
    # Jdet = J[0][0]*J[1][1]-J[0][1]*J[1][0]
    Jinv = np.linalg.inv(J)
    return Jinv,Jdet

def Bmatrix(r,s,Jinv):# 求B
    dNdr = diffNdr(r, s)
    dNds = diffNds(r, s)

    B1 = np.matrix([[1,0,0,0],[0,0,0,1],[0,1,1,0]])
    B2 = np.zeros((4,4))
    B2[0:2,0:2] = Jinv
    B2[2:4,2:4] = Jinv
    B3 = np.zeros((4,8))
    B3[0,0] = dNdr[0]
    B3[0, 2] = dNdr[1]
    B3[0, 4] = dNdr[2]
    B3[0, 6] = dNdr[3]
    B3[1, 0] = dNds[0]
    B3[1, 2] = dNds[1]
    B3[1, 4] = dNds[2]
    B3[1, 6] = dNds[3]
    B3[2, 1] = dNdr[0]
    B3[2, 3] = dNdr[1]
    B3[2, 5] = dNdr[2]
    B3[2, 7] = dNdr[3]
    B3[3, 1] = dNds[0]
    B3[3, 3] = dNds[1]
    B3[3, 5] = dNds[2]
    B3[3, 7] = dNds[3]

    B = B1*B2*B3
    return B

def planeStressC(E,nu):# 弹性系数矩阵
    C = np.zeros((3,3))
    cons = E/(1+nu)
    C[0, 0] = C[1, 1] = cons*1/(1-nu)
    C[0, 1] = C[1, 0] = cons * nu / (1 - nu)
    C[2, 2] = cons * 1 / 2
    return C

class K_element(object):
    def __init__(self,i,j,k,l):# 定义一个单元刚度矩阵的类，将索引值加入其中
        self.k = k
        self.l = l
        self.i = i
        self.j = j
        self.K = func_k(i,j,k,l)


def func_k(i,j,k,l):# 根据参数得到4个单元刚度矩阵
    intPoint = [-1 / sqrt(3), 1 / sqrt(3)]  # 二阶高斯点坐标
    weight = [1.0, 1.0]  # 权重
    E = 1 # 弹性模量
    nu = 0.3 # 泊松比
    C = planeStressC(E,nu)
    x0 = [-1,0,1,-1,0,1,-1,0,1]
    y0 = [-1,-1,-1,0,0,0,1,1,1]
    x = [x0[i - 1], x0[j - 1], x0[k - 1], x0[l - 1]]
    y = [y0[i - 1], y0[j - 1], y0[k - 1], y0[l - 1]]
    K = np.zeros((8,8))
    for j in range(0, 2): # 数值积分求K
        for i in range(0, 2):
            r = intPoint[i]
            s = intPoint[j]
            Jinv, Jdet = jacobian(x, y, r, s)
            B = Bmatrix(r, s, Jinv)
            BT = np.transpose(B)
            tmp = BT*C*B*Jdet
            K = K + tmp
    return K


def matrix_assembly(kk, Elementset):# 总刚度矩阵组装
    for e in Elementset:
        i, j, k, l= e.i, e.j, e.k, e.l
        for m in range(0, 2):
            for n in range(0, 2):# 将16个2x2矩阵按照索引值加入总刚度矩阵中
                kk[2*(i - 1)+m,2*(i - 1)+n] += e.K[m,n]
                kk[2*(j - 1)+m,2*(i - 1)+n] += e.K[2+m,n]
                kk[2*(k - 1)+m,2*(i - 1)+n] += e.K[4+m,n]
                kk[2 * (l - 1)+m,2 * (i - 1)+n] += e.K[6+m,n]
                kk[2*(i - 1)+m,2*(j - 1)+n] += e.K[m,2+n]
                kk[2*(j - 1)+m,2*(j - 1)+n] += e.K[2+m,2+n]
                kk[2*(k - 1)+m,2*(j - 1)+n] += e.K[4+m,2+n]
                kk[2 * (l - 1)+m,2*(j - 1)+n] += e.K[6+m,2+n]
                kk[2*(i - 1)+m,2*(k - 1)+n] += e.K[m,4+n]
                kk[2*(j - 1)+m,2*(k - 1)+n] += e.K[2+m,4+n]
                kk[2*(k - 1)+m,2*(k - 1)+n] += e.K[4+m,4+n]
                kk[2 * (l - 1)+m,2*(k - 1)+n] += e.K[6+m,4+n]
                kk[2*(i - 1)+m,2 * (l - 1)+n] += e.K[m,6+n]
                kk[2*(j - 1)+m,2 * (l - 1)+n] += e.K[2+m,6+n]
                kk[2*(k - 1)+m,2 * (l - 1)+n] += e.K[4+m,6+n]
                kk[2 * (l - 1)+m,2 * (l - 1)+n] += e.K[6+m,6+n]
    return kk

SE_1 = K_element(1, 2, 5, 4)
print("单元1的刚度矩阵：{}".format(SE_1.K))
SE_2 = K_element(2, 3, 6, 5)
print("单元2的刚度矩阵：{}".format(SE_1.K))
SE_3 = K_element(5, 6, 9, 8)
print("单元3的刚度矩阵：{}".format(SE_1.K))
SE_4 = K_element(4, 5, 8, 7)
print("单元4的刚度矩阵：{}".format(SE_1.K))

Elementset = []
Elementset.append(SE_1)
Elementset.append(SE_2)
Elementset.append(SE_3)
Elementset.append(SE_4)
# 创建一个总体刚度矩阵的列表
kk = np.zeros((18, 18))
# 然后得到组合后的刚度矩阵
matrix_assembly(kk, Elementset)
print("组合后的总刚度矩阵：{}".format(kk))

得到结果如下：

3、设置力和位移边界条件求解各个点的力和位移

3.1 边界条件和求解原理如下：

3.2 源代码如下，经过求解得到9的点的力和位移，并且以图表的形式画出：

# 求U和F
# 边界条件
# U = np.matrix([[0],[0],["u_unknow"],["u_unknow"],[0],[0],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"],["u_unknow"]],dtype=object)
# F = np.matrix([["F_unknow"],["F_unknow"],[0],[-1000],["F_unknow"],["F_unknow"],[-1000],[0],[0],[-1000],[1000],[0],[-1000],[0],[0],[1000],[1000],[0]],dtype=object)

# LU解线性方程组
def LU(A):
    '''
    生成值全位0的U矩阵，和单位矩阵L
    '''
    L = np.eye(len(A))
    U = np.zeros(np.shape(A))
    for r in range(1, len(A)):  # 求U的第一行和L的第一列
        U[0, r - 1] = A[0, r - 1]
        L[r, 0] = A[r, 0] / A[0, 0]
    U[0, -1] = A[0, -1]
    for r in range(1, len(A)):  # 先求U再求L
        for i in range(r, len(A)):
            delta = 0
            for k in range(0, r):  # 求∑(???∗???)
                delta += L[r, k] * U[k, i]
            U[r, i] = A[r, i] - delta

            for i in range(r + 1, len(A)):  # 求L矩阵
                theta = 0
                for k in range(0, r):  # 求∑(?i?∗??r)
                    theta += L[i, k] * U[k, r]
                L[i, r] = (A[i, r] - theta) / U[r, r]
    return L,U
def my_LUsolve(A,b):
    L, U = LU(A) # 得到L和U
    '''print("L={}".format(L))
    print("U={}".format(U))'''
    # 求解线性方程LY=b
    n = len(A)
    y = np.zeros((n, 1))
    b = np.array(b).reshape(n,1) # 把b列表格式变成向量格式
    for i in range(len(A)):
        t = 0
        for j in range(i):
            t += L[i][j]* y[j][0]
        y[i][0] = b[i][0] - t
    # print("y={}".format(y))
    # 求解UX=Y
    X = np.zeros((n, 1))
    for i in range(len(A)-1,-1,-1):
        t = 0
        for j in range(i+1,len(A)):
            t += U[i][j]*X[j][0]
        t = y[i][0] - t
        if t != 0 and U[i][i] == 0:
            return 0
        X[i] = t/U[i][i]
    # print("X={}".format(X))
    return X

new2_F = np.matrix([[0],[-1000],[-1000],[0],[0],[-1000],[1000],[0],[-1000],[0],[0],[1000],[1000],[0]])
new_kk_row = np.delete(kk, [0, 1, 4, 5], axis=0)
new_kk = np.delete(new_kk_row, [0, 1, 4, 5], axis=1)# 在原总刚度下删除U=0所在的行和列，得到一个新的矩阵
new2_U = my_LUsolve(new_kk, new2_F)
U1 = np.zeros((18, 1))
U1[2, 0] = new2_U[0, 0]
U1[3, 0] = new2_U[1, 0]
for i in range(12):
    U1[i+6, 0] = new2_U[i+2, 0]
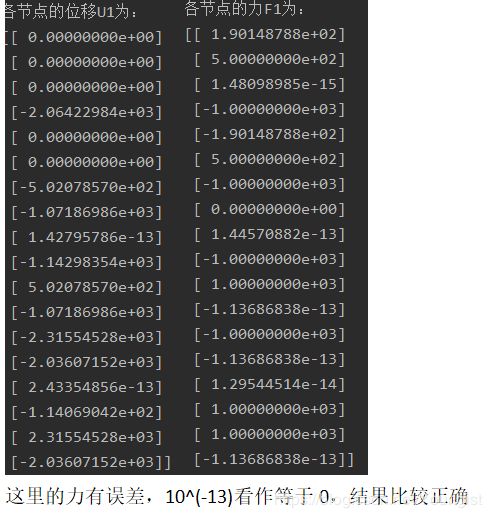
print("各节点的位移U1为：")
print(U1)
print(np.shape(kk))
print(np.shape(U1))
print("各节点的力F1为：")
F1 = kk*np.matrix(U1)
print(F1)

U_point = [] # 求各个点的位移
for i in range(0, 18, 2):
    Udet = sqrt((U1[i])*(U1[i])+(U1[i+1])*(U1[i+1]))
    U_point.append(Udet)
print("各个点的位移为：{}".format(U_point))

F_point = [] # 求各个点的力
for i in range(0, 18, 2):
    Fdet = sqrt((F1[i][0])*(F1[i][0])+(F1[i+1][0])*(F1[i+1][0]))
    F_point.append(Fdet)
print("各个点的力为：{}".format(F_point))

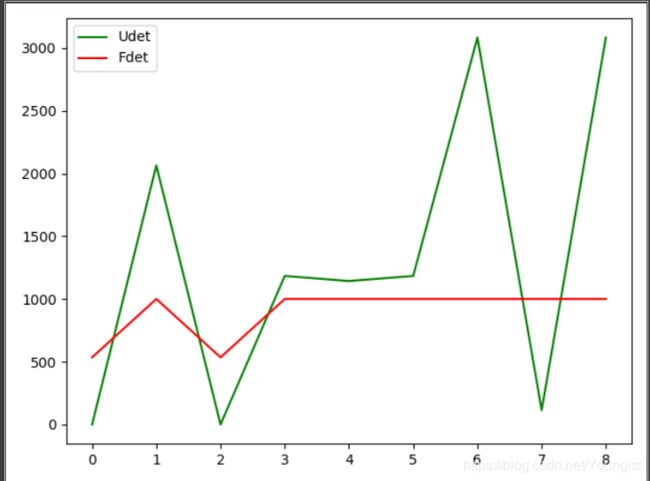
plt.plot(U_point,color='g',label='Udet' )
plt.plot(F_point,color = 'r',label = 'Fdet')
plt.legend(loc=' best')
plt.show()

4、 得到的结果如下：