SLAM中的marginalization 和 Schur complement
在视觉SLAM的很多论文中,会大量或者偶尔出现marginalization这个词(翻译为边缘化),有的论文是特地要用它,比如sliding window slam [2], okvis [3], dso [4]。而有的论文是简单的提到,比如g2o[1],orbslam。因此,很有必要对这个概念进行了解。
##marg 基础
在我们这个工科领域,它来源于概率论中的边际分布(marginal distribution)。如从联合分布p(x,y)去掉y得到p(x),也就是说从一系列随机变量的分布中获得这些变量子集的概率分布。回忆了这个概率论中的概念以后,让我们转到SLAM的Bundle Adjustment上,随着时间的推移,路标特征点(landmark)和相机的位姿pose越来越多,BA的计算量随着变量的增加而增加,即使BA的H矩阵是稀疏的,也吃不消。因此,我们要限制优化变量的多少,不能只一味的增加待优化的变量到BA里,而应该去掉一些变量。那么如何丢变量就成了一个很重要的问题!比如有frame1,frame2,frame3 以及这些frame上的特征点pt1…ptn。新来了一个frame4,为了不再增加BA时的变量,出现在脑海里的直接做法是把frame1以及相关特征点pt直接丢弃,只优化frame2,frame3,frame4及相应特征点。然而,这种做法好吗?
Gabe Sibley [2]在他们的论文中就明确的说明了这个问题。直接丢掉变量,就导致损失了信息,frame1可能能更多的约束相邻的frame,直接丢掉的方式就破坏了这些约束。在SLAM中,一般概率模型都是建模成高斯分布,如相机的位姿都是一个高斯分布,轨迹和特征点形成了一个多元高斯分布p(x1,x2,x3,pt1…),然后图优化或者BA就从一个概率问题变成一个最小二乘问题。因此,从这个多元高斯分布中去掉一个变量的正确做法是把他从这个多元高斯分布中marginalize out.
这marginalize out具体该如何操作呢?Sliding widow Filter [2]中只是简单的一句应用Schur complement(舍尔补). 我们知道SLAM中的图优化和BA都是最小二乘问题,如下图所示(ref.[1])

pose graph和BA中,误差函数 e e e是非线性的,这个非线性最小二乘问题可以通过高斯牛顿迭代求得,即
H δ x = b H\delta x= b Hδx=b
其中 H = J T W J , b = J W e H=J^TWJ, b=JWe H=JTWJ,b=JWe, J J J是误差对位姿等的雅克比, W W W是权重。一般这个H矩阵也称为信息矩阵,并且H矩阵是稀疏的,这些都是SLAM中的基础知识,我这里啰嗦了下。
要求解这个线性方程,可以用QR分解什么的,但是这里我们关注marginalize. 也就是说只去求解我们希望保留的变量,那些我们要marg的变量就不关心了,从而达到减少计算的目的。假设变量x中可以分为保留部分和marg部分,那么上面的线性方程可以写成如下形式:
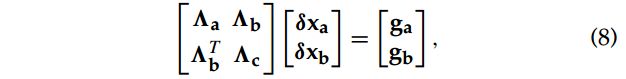
这里我们要marg掉 x a x_a xa,而计算 x b x_b xb, 对上面这个方程进行消元得到:
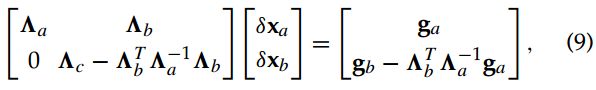
其中 Λ b T Λ a − 1 Λ b \Lambda ^T_{b}\Lambda ^{-1}_{a}\Lambda _{b} ΛbTΛa−1Λb就称为 Λ a \Lambda _{a} Λa在 Λ b \Lambda _{b} Λb中的schur complement。有了这个上三角形式,我们就可以直接计算出 δ x b \delta x_{b} δxb了:
( Λ c − Λ b T Λ a − 1 Λ b ) δ x b = g b − Λ b T Λ a − 1 g a (\Lambda _{c}-\Lambda ^T_{b}\Lambda ^{-1}_{a}\Lambda _{b} )\delta x_{b}=g_b-\Lambda ^T_{b}\Lambda ^{-1}_{a}g_a (Λc−ΛbTΛa−1Λb)δxb=gb−ΛbTΛa−1ga
这样我们就能够迭代的更新部分变量,从而维持计算量不增加。在上面这个过程中,我们要注意,构建出来的Hx=b是利用了marg变量的信息,也就是说我们没有人为的丢弃约束,所以不会丢失信息,但是计算结果的时候,我们只去更新了我们希望保留的那些变量的值。在slam的过程中,BA不断地加入新的待优化的变量,并marg旧的变量,从而使得计算量维持在一定水平。这就是sliding window filter, okvis, dso这些论文中marg的应用。
当然,上面如果你想去更新marg变量也是可以的,不是说只能计算 x b x_b xb,因为方程是完整的,只是这里我们强调只计算 x b x_b xb。在g2o[1]的论文III-D部分,公式(25),(26)就是两部分都计算:

他这里是把变量分为相机位姿 x p x_p xp和特征点 x l x_l xl两部分,然后利用schur complement先算相机位姿,再算特征点位姿,充分利用H矩阵的稀疏性加速计算。g2o算ba的example程序里就是把特征点设置为marginalize,这个在orbslam的local ba里也能看到。然而这种用法不像我们前面提到的那样真正marg out变量,这里被设为marg的那些特征点还是计算了值。这和我们这里的主题是有点点不同的。
让我们从g2o中回到marginalize的本意上去,也就是说只更新部分变量,而不是所有变量。从上面的过程中,貌似marg也就那么回事,简单得很,实际上水很深,具体后面再提。现在让我们从概率的角度去了解下这个东西的背后,幸好有人提了这个问题stackoverflow link。

一句话总结如下:要把一部分变量从多元高斯分布从分离出来,其实协方差矩阵很好分离,难分的是信息矩阵(协方差的逆),因为我们通常在SLAM里知道的是H矩阵,而不是协方差矩阵。对于H矩阵的分离,需要用到schur complement来分割。比如分割后能得到
![]()
##marg 深入
通过上面的知识点,我们知道了marg的过程,以及使用schur complement来实现。然而[2]论文中对marg的过程进行了更详尽的分析。这些分析总结出了一些技巧,也就是okvis和dso论文中常常提到的为了保持H矩阵的稀疏性,我们采取了这样那样的规则。
视觉SLAM的Bundle Adjustment中的Hessian矩阵一般是如下的结构
![]()
左上角是雅克比对pose求导并对应相乘得到的,右下角是和特征点相关的,绿色部分是pose和landmark之间交叉的。现在我们来看一看marg一个变量是如何影响H矩阵的稀疏性的。假设有四个相机pose,以及6个特征点 x m x_m xm,每个pose观测到三个特征点landmark,图关系如下:

现在我们先把pose1给marg掉,然后再marg掉特征点 x m 1 x_{m1} xm1,看看H矩阵如何变化。

图1是原始的H矩阵,这个图中的H和前面的H矩阵不一样,这里右下角是pose相关部分,左上角是特征点相关部分。图2是把H矩阵中和pose1相关的部分移动到H矩阵的左上角。图3是marg掉pose1以后的H矩阵,用斜线标记的部分是待marg的特征点1. 实际上marg以后的图3对应前面求 δ x b \delta x_b δxb时的矩阵 ( Λ c − Λ b T Λ a − 1 Λ b ) (\Lambda _{c}-\Lambda ^T_{b}\Lambda ^{-1}_{a}\Lambda _{b} ) (Λc−ΛbTΛa−1Λb)。可以看到图3和图2中去掉斜线部分对比的话,变得稠密了。也就是说,marg掉一个位姿,会使得剩余的H矩阵中有3个地方会fill-in, 图3中的颜色加重区域:a. 所有在位姿1能够观测到的landmark之间会fill-in,图3的左上角应该和图2中一样是6个小方块,结果marg以后和pose1相关的那3个小的方块变成了一个稠密的块。b. 和marg掉的pose1相连的pose2, 右下角区域中的左上角颜色加重部分。c. pose2跟被pose1观测到的那些特征点之间也会有fill-in. 这时候,图关系变成了入下:

注意,xm1,xm2,xm3之间相互连接起来了,并且xm1和xp2之间也连起来了,对应上面提到的这三点。接下来,就是marg掉特征xm1,H矩阵由3变成了4. 这时候的fill-in也是颜色加重区域。由于marg掉xm1之前不被任何其他pose观测到,而marg掉pose1以后,现在只和pose2相连,因此引入的fill-in还不是很多。这时候对应的图关系如下:

marg特征点1的这个过程这也给我们启示,就是marg特征点的时候,我们要marg那些不被其他帧观测到的特征点。因为他们不会显著的使得H变得稠密。对于那些被其他帧观测到的特征点,要么就别设置为marg,要么就宁愿丢弃,这就是okvis和dso中用到的一些策略。
虽然上面这些总结在marg的过程中很重要,但是我认为更重要的是关于marg过程中consistency的讨论。dso论文中提到计算H矩阵的雅克比时用FEJ (first estimate jacobian) [5],okvis论文中也提到要
fix the linearization point around x 0 x_0 x0, the value of x x x at the time of marginalization.
因为迭代过程中,状态变量会被不断更新,计算雅克比时我们要fix the linearization point。 所谓linearization point就是线性化时的状态变量,即求雅克比时的变量,因为计算雅克比是为了泰勒展开对方程进行线性化。我们要固定在点x0(marg 时的状态变量)附近去计算雅克比,而不是每次迭代更新以后的x。[7]是2016年IROS的论文,对这个原因表述的很清楚也容易阅读(套用张腾大神的话包教包会,感谢他的推荐), [6][5]是两篇年代更久一点的论文,这两篇论文都很有裨益,但是难读,单单这个consistency分析就值得仔细去看看,因为它直接涉及到优化结果。
为了更直观的理解上述这个结果,“泡泡机器人”里部分成员对这个过程进行了讨论,TUM的杨楠请教了其师兄DSO作者Engel。Engel用一张图就解释了这个过程:
![]()
在刘毅(稀疏毅),王京,晓佳等人讨论下,对这张图作出了如下解释:四张能量图中,第一张是说明能量函数 E E E由两个同样的非线性函数 E 1 E_1 E1和 E 2 E_2 E2组成,我们令函数 E = 0 E=0 E=0,这时方程的解为 x y = 1 xy=1 xy=1,对应图中深蓝色的一条曲线。第二张能量函数图中的 E 1 ′ E'_1 E1′对应函数 E 1 E_1 E1在点(0.5,1.4)处的二阶泰勒展开,第三张能量函数图中的 E 2 ′ E'_2 E2′对应函数 E 2 E_2 E2在点(1.2,0.5)处的二阶泰勒展开。注意这两个近似的能量函数 E 1 ′ E'_1 E1′和 E 2 ′ E'_2 E2′是在不同的线性点附近对原函数展开得到的。最后一张图就是把这个近似得到的能量函数合并起来,对整个系统 E E E的二阶近似。从第四个能量函数图中,我们发现一个大问题,能量函数为0的解由以前的一条曲线变成了一个点,不确定性的东西变得确定了,专业的术语叫不可观的状态变量变得可观了,说明我们人为的引入了错误的信息。回到marg过程,上面这个例子告诉我们,marg时,被marg的那些变量的雅克比已经不更新了,而此时留在滑动窗口里的其他变量的雅克比要用和marg时一样的线性点,就是FEJ去算,不要用新的线性点了。有了这些基础以后,大家可以再去看看王京,张腾大神们在知乎上关于FEJ更理论的表述,链接请戳。
由于我还没真正接触过first estimate jocabian的代码,所以对它理解还是停留在paper上,可能理解有偏差,还需要读完dso的代码,加深理解以后,我再对博客进行补充。如果有读者很熟悉这部分,欢迎指教,谢谢。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
ref:
[1] 《 g2o: A General Framework for Graph Optimization 》
[2] 《 Sliding Window Filter with Application to Planetary Landing 》
[3] 《 Keyframe-Based Visual-Inertial SLAM Using Nonlinear Optimization 》ijrr 2014 这个详细些
[4] 《 Direct Sparse Odometry 》
[5] 《Analysis and Improvement of the Consistency of Extended Kalman Filter based SLAM》
[6] 《Motion Tracking with Fixed-lag Smoothing: Algorithm and Consistency Analysis》
[7] 《Decoupled, Consistent Node Removal and Edge Sparsification for Graph-based SLAM》