SLAM之相机标定
0 写在前面
此篇博客,包括之后的一些SLAM系列博客,其实都是高翔博士的《视觉SLAM十四讲》读书笔记,在此向高博所做的工作致敬。对SLAM初学者而言,《视觉SLAM十四讲》非常适合入门,而且高博在深蓝学院开设了《SLAM理论与实践》课程,以视频+作业+答疑的模式,如果能够坚持下来,把每次作业和最后的大作业都完成,就可以说入门了。
1 实验背景
相机将三维世界中的坐标点(单位为米)映射到二维图像平面(单位为像素)的过程能够用一个几何模型进行描述。这个模型有很多种,其中最简单的称为针孔模型。针孔模型很常用,而且是有效的模型,它描述了一束光线通过针孔之后,在针孔背面投影成像的关系。遗憾的是,真实的针孔由于不能为快速曝光收集足够的光线,因此使用透镜来收集更多的光线。由于透镜的存在,会使得光线投影到成像平面的过程中会产生畸变。
本实验将利用摄像机标定(camera calibration),来矫正(数学方式)因使用透镜而给针孔模型带来的主要误差。摄像机标定的重要性还在于它是摄像机测量与真实三维世界测量的联系桥梁。摄像机标定的过程既给出摄像机几何模型,也给出透镜的畸变的模型。这两个模型定义了相机的内参数(intrinsic parameter)。
2 实验目的
(1) 掌握单目摄像机标定的方法,理解针孔摄像机模型和畸变模型。
(2) 掌握OpenCV标定函数的使用,完成一幅畸变图像的去畸变处理。
3 实验环境
硬件平台:惠普笔记本电脑
处理器:Intel® Core™ i5-7300HQ CPU @ 2.50GHz × 4
操作系统:ubuntu 14.04 LTS
机器人操作系统:ROS Indigo
4 理论基础
4.1 针孔相机模型
小孔模型能够把三维世界中的物体投影到一个二维成像平面。同理,可以用这个简单的模型来解释相机的成像模型。如图4-1所示。
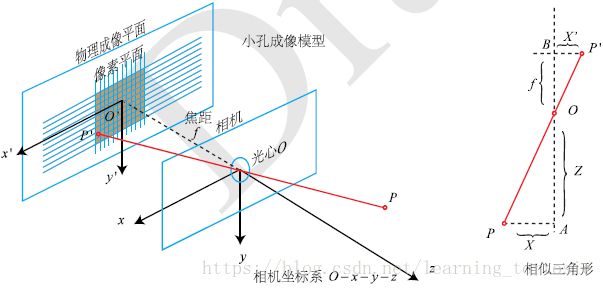
对这个简单的针孔模型进行几何建模。设 O − x − y − z O-x-y-z O−x−y−z为相机坐标系,习惯上让z轴指向相机前方, x x x向右, y y y向下。 O O O为摄像机的光心,也是针孔模型中的针孔。现实世界的空间点 P P P,经过小孔 O O O投影之后,落在物理成像平面 O ′ − x ′ − y ′ − z ′ O'-x'-y'-z' O′−x′−y′−z′上,成像点为 P ′ P' P′。设 P P P的坐标为 [ X , Y , Z ] T [X,Y,Z]^T [X,Y,Z]T, P ′ P' P′为 [ X ′ , Y ′ , Z ′ ] T [X',Y',Z']^T [X′,Y′,Z′]T,并且设物理成像平面到小孔的距离为 f f f(焦距)。那么,根据三角形相似关系,有:
![]()
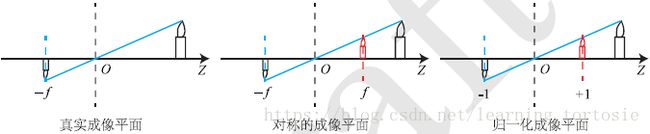
其中负号表示成的像是倒立的。为了简化模型,可以将成像平面对称到相机前方,和三维空间点一起放在摄像机坐标系的同一侧,如图4-2中间的样子所示。这样可以把公式中的负号去掉,使式子更加简洁:
![]()
整理得:
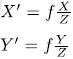
上式描述了点 P P P和它的像之间的空间关系。不过,在相机中,最终获得的是一个个的像素,这需要在成像平面上对像进行采样和量化。为了描述传感器将感受到的光线转换成图像像素的过程,在物理成像平面上固定一个像素平面 o − u − v o-u-v o−u−v。在像素平面上得到了 P ′ P' P′的像素坐标: [ u , v ] T [u,v]^T [u,v]T。
像素坐标系通常的定义方式是:原点 o ’ o’ o’位于图像的左上角, u u u轴向右与 x x x轴平行, v v v轴向下与 y y y轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。设像素坐标在u轴上缩放了 α α α倍,在 v v v上缩放了 β β β倍。同时,原点平移了 [ c x , c y ] T [cx , cy ]^T [cx,cy]T。那么, P ’ P’ P’点的坐标与像素坐标 [ u , v ] T [u,v]^T [u,v]T的关系为:
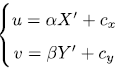
整理得:
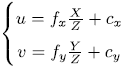
把该式写成矩阵形式,会更加简洁,不过左侧需要用到齐次坐标:
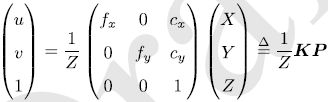
按照传统的习惯,把 Z Z Z挪到左侧:

该式中,把中间的量组成的矩阵称为相机的内参数矩阵 K K K。通常认为,相机的内参在出厂之后是固定的,不会在使用过程中发生变化。有的相机生产商会告诉相机的内参,而有时需要自己确定相机的内参,也就是所谓的标定。标定算法已成熟,在网络上可以找到大量的标定教学。
##4.2 畸变
为了获得好的成像效果,在相机前方加了透镜。透镜的加入对成像过程中光线的传播会产生新的影响:一是透镜自身的形状对光线传播的影响,二是在机械组装过程中,透镜和成像平面不可能完全平行,这也会使得光线穿过透镜投影到成像平面时的位置发生变化。
由透镜形状引起的畸变称之为径向畸变。它们主要分为两大类,桶形畸变和枕形畸变,如图4-3所示。
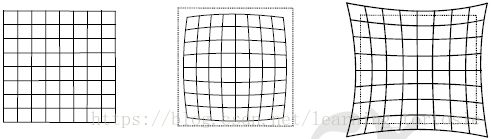
切向畸变如图4-4所示。
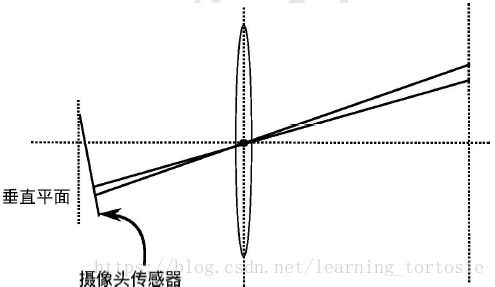
平面上的任意一点p可以用笛卡尔坐标表示为 [ x , y ] T [x,y]^T [x,y]T,也可以写成极坐标的形式 [ r , θ ] T [r,θ]^T [r,θ]T,
其中 r r r表示点 p p p离坐标系原点的距离, θ θ θ表示和水平轴的夹角。
对于径向畸变,可以用一个多项式函数来描述畸变前后的坐标变化:
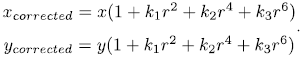
其中 [ x , y ] T [x,y]^T [x,y]T是为纠正的点的坐标, [ x c o r r c c t e d , y c o r r c c t e d ] T [x_{corrccted},y_{corrccted}]^T [xcorrccted,ycorrccted]T是纠正后的点的坐标,它们都是归一化平面上的点。
对于切向畸变,有:
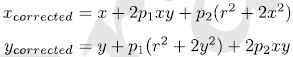
通过五个畸变系数找到相机坐标系中的一点在像素平面上的正确位置:
- 将三维空间点投影到归一化平面。设它的归一化坐标为 [ x , y ] T [x,y]^T [x,y]T。
- 对归一化平面上的点进行径向畸变和切向畸变纠正。

3.将纠正后的点通过内参数矩阵投影到像素平面,得到改点在图像上的正确位置。

5 实验步骤
可以通过matlab,OpenCV,ROS三种方式进行相机标定。这里使用基于ROS的方式标定单目相机。
ROS提供了camera_calibration Package,通过这个Package可以使用棋盘标定板对单目和双目相机进行标定。
以下步骤基本是ROS wiki教程的翻译,更多细节请移步以上链接。
另外推荐一个标定工具Kalibr,可以实现Multiple camera calibration、Camera-IMU calibration、Rolling Shutter Camera calibration。
5.1 准备工作
(1)准备一个已知尺寸的标定板,本实验使用的是8X6,边长为108mm的棋盘标定板。由于标定过程使用的是棋盘内部的角点进行,所以实际上我们使用的是9X7的棋盘标定板 。
(2)确保标定环境拥有一个5m×5m的无遮挡环境。
(3)一个通过ROS发布图像的单目相机。
5.2 编译
首先获取依赖关系并编译驱动程序。
$ rosdep install camera_calibration
确保单目相机正在通过ROS发布图像。列出主题来检查图像是否已发布:
$ rostopic list
这会显示所有已发布的主题,检查是否有image_raw主题。大多数ROS相机驱动程序提供的默认主题是:
/camera/camera_info
/camera/image_raw
5.3 运行标定节点
加载将要标定的图像主题:
$ rosrun camera_calibration cameracalibrator.py --size 8x6 --square 0.108 image:=/camera/image_raw camer:=/camera
此命令运行标定结点的python脚本,其中 :
(1)--size 8x6 为当前标定板的大小
(2)--square 0.108为每个棋盘格的边长
(3)image:=/camera/image_raw标定当前订阅图像来源自名为/camera/image_raw的topic
(4)camera:=/camera为摄像机名
这将打开标定窗口,如图5-1所示。

5.4 移动棋盘标定板
为了达到良好的标定效果,需要在摄像机周围移动标定板,并完成以下基本需求:
(1)移动标定板到画面的最左、右,最上、下方。
(2)移动标定板到视野的最近和最远处。
(3)移动标定板使其充满整个画面。
(4)保持标定板倾斜状态并使其移动到画面的最左、右,最上、下方 。

当标定板移动到画面的最左、右方时,此时,窗口的x会达到最小或满值。同理,y指示标定板的在画面的上下位置,size表示标定板在视野中的距离。每次移动之后,请保持标定板不动直到窗口出现高亮提示。当calibration按钮亮起时,代表已经有足够的数据进行摄像头的标定,此时请按下calibration并等待一分钟左右。如图5-3所示。

5.5 获得标定结果
在标定完成后,终端会输出校正结果。如下所示:
D = [-0.33758562758914146, 0.11161239414304096, -0.00021819272592442094, -3.029195446330518e-05]
K = [430.21554970319971, 0.0, 306.6913434743704, 0.0, 430.53169252696676, 227.22480030078816, 0.0, 0.0, 1.0]
R = [1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0]
P = [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0]
# oST version 5.0 parameters
[image]
width
640
height
480
[narrow_stereo/left]
camera matrix
430.215550 0.000000 306.691343
0.000000 430.531693 227.224800
0.000000 0.000000 1.000000
distortion
-0.337586 0.111612 -0.000218 -0.000030 0.0000
rectification
1.000000 0.000000 0.000000
0.000000 1.000000 0.000000
0.000000 0.000000 1.000000
projection
1.000000 0.000000 0.000000 0.000000
0.000000 1.000000 0.000000 0.000000
0.000000 0.000000 1.000000 0.000000
其中,K为相机内参矩阵,distortion为畸变系数矩阵。
5.6 图像去畸变
通过相机标定,得到了相机内参矩阵和畸变系数矩阵,这样便可以对图形进行去畸变操作,得到畸变前的图像。测试图像如图5-4所示。

从图5-4可以看出,实际的柱子、箱子的直线边缘在图像中被扭曲成了曲线,这就是由相机畸变造成的。
经过相机标定后,得到相机内参和畸变系数,根据4.5中描述的步骤编程实现图像的去畸变。
6 实验结果
去畸变后的图像如图6-1所示。

从图6-1可以看出,图5-4中曲线恢复成了直线,证明了图像去畸变操作的正确性。
7 总结
通过本次实验,我理解了针孔相机模型、透镜的畸变模型,以及世界坐标系、相机坐标系、像素坐标系的转化关系。掌握了使用ROS提供的包对相机进行标定的方法,然后通过标定得到相机内参和畸变系数,对图像进行去畸变操作。
在图像去畸变中,没有使用OpenCV自带的去畸变函数,而是自己根据理论去编程实现,加深了对去畸变过程的理解。
附录
程序源码
#include
using namespace std;
string image_file = "./test.png"; // 请确保路径正确
int main(int argc, char **argv) {
// 本程序需要自己实现去畸变部分的代码,尽管可以调用OpenCV的去畸变,但自己实现一遍有助于理解。
// 畸变参数
double k1 = -0.28340811, k2 = 0.07395907, p1 = 0.00019359, p2 = 1.76187114e-05;
// 内参
double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;
cv::Mat image = cv::imread(image_file,0); // 图像是灰度图,CV_8UC1
int rows = image.rows, cols = image.cols;
cv::Mat image_undistort = cv::Mat(rows, cols, CV_8UC1); // 去畸变以后的图
// 计算去畸变后图像的内容
for (int v = 0; v < rows; v++)
for (int u = 0; u < cols; u++) {
double u_distorted = 0, v_distorted = 0;
//按照公式,计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted)
double x = (u-cx)/fx;
double y = (v-cy)/fy;
double r = sqrt(x^2+y^2);
double x_distorted = x*(1+k1*r^2+k2*r^4)+2*p1*x*y+p2*(r^2+2*x^2);
double y_distorted = y*(1+k1*r^2+k2*r^4)+2*p2*x*y+p1*(r^2+2*y^2);
u_distorted = fx*x_distorted+cx;
v_distorted = fy*y_distorted+cy;
// 赋值 (最近邻插值)
if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows) {
image_undistort.at(v, u) = image.at((int) v_distorted, (int) u_distorted);
} else {
image_undistort.at(v, u) = 0;
}
}
// 画图去畸变后图像
cv::imshow("image undistorted", image_undistort);
cv::waitKey();
return 0;
}