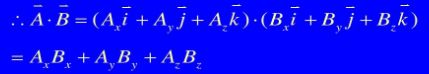深蓝学院-视觉SLAM课程学习课后题
一. 第一节课习题# 标题
1.熟悉linux

(1)可以通过 sudo apt-get install <软件名>的方式安装软件
当自己下载了软件压缩包之后(tar.gz文件),可以解压后,通过cd命令进入压缩包目录,输入编译文件命令:./configure,然后是命令:make,完成之后通过make install命令完成安装。
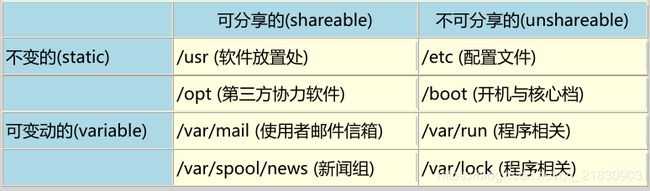
软件安装位置:
一般安装在/usr下,里面很多文件夹,根据文件的类型,分门别类,不是一个软件一个文件夹。以前老版本的Linux习惯放在/usr/local目录下。
部分软件放在/opt下,则是一个软件统一在一个文件夹下。/opt目录专门是用来给第三方软件放置文件的,比如一些压缩包解压的软件都放在这里。
例如:
网易云音乐 安装在/usr/lib/netease-cloud-music
Chrome 放在/opt/google/chrome
2.linux的环境变量及其设置
环境变量通俗讲是操作系统或程序执行时候默认设定的参数,比如path路径变量。当要执行某个命令或程序的时候默认寻找的路径。
环境变量的类型:
永久变量:通过修改配置文件,配置之后变量永久生效
临时性变量:使用命令如export等命令设置,设置之后马上生效,关闭shell后失效。
[root@mail ~]#env 显示所有变量
按照影响范围划分:
用户变量(局部变量):修改的设置只对某个用户的路径或执行起作用
系统变量(全局变量):影响范围是整个系统
查看环境变量,如路径变量path:
[root@mail ~]#echo $PATH
常见的设置方法:
使用export命令,以指定php和mysql执行的路径变量为例:
[root@mail ~]#export PATH=$PATH:/usr/local/php/bin 为php环境
[root@mail ~]#export PATH=$PATH:/usr/local/mysql/bin 为mysql环境
注:这只是临时变量的设置方法
永久设置环境,在当前用户目录下:
gedit ~/.bashrc 打开该文件将环境变量写入 示例如下:

3.linux根目录下的结构:
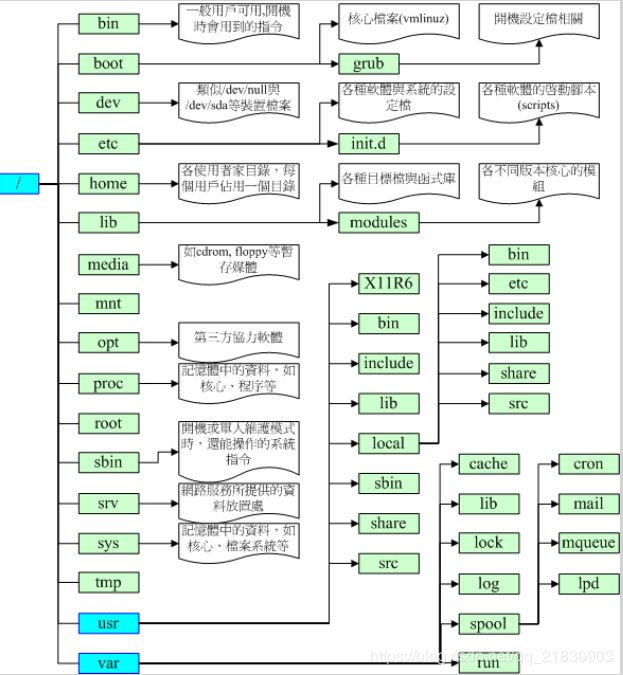
详见鸟哥私房菜基础篇192页
请问底下的目彔主要放置什么数据:
/etc/, /etc/init.d, /boot, /usr/bin, /bin, /usr/sbin, /sbin, /dev, /var/log
/etc/:几乎系统的所有配置文件案均在此,尤其 passwd,shadow
/etc/init.d:系统开机的时候加载朋务的 scripts 的摆放地点
/boot:开机配置文件,也是预讴摆放核心 vmlinuz 的地方
/usr/bin, /bin:一般执行档摆放的地方
/usr/sbin, /sbin:系统管理员常用挃令集
/dev:摆放所有系统装置档案的目彔
/var/log:摆放系统注册表档案的地方
4.关于权限设置的基础知识:
利用 ls -l 显示的文件属怅中,第一个字段是档案的权限,共有十个位,第一个位是文件类型,
接下来三个为一组共三组,为***使用者、群组、其他人***的权限,权限有 r,w,x 三种;
![]()
如果档名前多一个『 . 』,则代表这个档案为『隐藏档』;
更改档案的群组支持可用 chgrp,修改档案的拥有者可用 chown,修改档案的权限可用 chmod
chmod 修改权限的方法有两种,分别是符号法和数字法,数字法中 r,w,x 分数为 4,2,1;
可以根据分数的设置来设置不同用户组对于文件的使用权限
对档案来讲,权限的效能为:
r:可读取此一档案的实际内容,如读取文本文件的文字内容等;
w:可以编辑、新增戒者是修改该档案的内容(但不含删除该档案);
x:该档案具有可以被系统执行的权限。
对目录来说,权限的效能为:
r (read contents in directory)
w (modify contents of directory)
x (access directory)
要开放目录给任何人浏觅时,应该至少也要给予 r 及 x 的权限,但 w 权限不可随便给;
owner = rwx = 4+2+1 = 7
group = rwx = 4+2+1 = 7
others= — = 0+0+0 = 0
我需要将一个档案的权限改为 -rwxr-xr-- 请问该如何下达指令?
**chmod 754 filename** 或 **chmod u=rwx,g=rx,o=r filename** 7:rwx 5:-wx 4:r--
-R : 进行递归(recursive)的持续变更,亦即连同次目录下的所有档案都会变更
5.若我需要更改一个档案的拥有者或群组,该用什么指令?

在本题中,改变a.sh文件的群组使用以下命令:
chgrp xiang a.sh
改变档案的拥有者:chown
chown [-R] 账号名称 档案或目录
chown [-R] 账号名称:组名 档案或目录
因而在本题中,可使用命令: chown xiang:xiang a.sh 完成拥有者和群组的更换
2.SLAM的文献阅读

1.SLAM的应用场合
SLAM(即时定位与地图构建)技术主要被运用于无人机、无人驾驶、机器人、AR、智能家居等领域,从各应用场景入手,促进消费升级。
机器人 激光+SLAM是目前机器人自主定位导航所使用的主流技术。
无人驾驶 无人驾驶利用激光雷达传感器(Velodyne、IBEO等)作为工具,获取地图数据,并构建地图
AR AR通过电脑技术,将虚拟的信息应用到真实世界,真实的环境和虚拟的物体实时地叠加到了同一个画面或空间同时存在。这一画面的实现,离不开SLAM技术的实时定位。
无人机 无人机在飞行的过程中需要知道哪里有障碍物,该怎么规避,怎么重新规划路线。显然,这是SLAM技术的应用。
2. SLAM中定位与建图的关系:
定位是需要周围环境的信息的,是借助周围地图信息来定位的; 建图又需要准确知道目前摄像机随着机器人的自身位置; 准确的定位需要准确的地图; 精准的地图构建又需要精准的位置信息;
是一个很耦合的问题。 所以,定位的同时需要建图。
3.SLAM的发展历史与阶段的划分:
(1)第一阶段:定位和建图分开研究的阶段;
(2)第二阶段:定位和建图在一起进行研究的阶段;
(3)第三阶段:开始运用摄像头的阶段(这里需要注意的是,之前由于计算机视觉的发展还不太到位,因此之前基本都是基于激光测距这种方法的)
(4)第四阶段:多元化的阶段(我之所以把这个阶段叫做多元化的阶段,是因为SLAM和深度学习的融合,视觉和惯性传感器的融合等解决方案不断的涌现,对于SLAM的发展可以说是起了极大的加速作用,也使得SLAM这个已经好几十年的老话题在今天又被大家重新认识,且重新投入努力和热情去对待。
4.SLAM领域的经典文献:
《LSD-SLAM: Large-Scale Direct Monocular SLAM》(直接法的代表性文章)
《ORB-SLAM:ORB-SLAM: a Versatile and Accurate Monocular SLAM System》(特阵法的代表性文章,后续的ORB-SLAM2还开发出单目、双目、RGB-D的开源代码,且代码形式很好,值得学习)
《VINS-Mono: A Robust and Versatile Monocular Visual Inertial State Estimator》(经典的视觉和IMU融合的方法,值得学习)
mkdir hello_test
cd hello_test
mkdir lib build
touch CMakeLists.txt
gedit CMakeLists.txt
hello_test目录下的内容:
PROJECT(hello)
ADD_SUBDIRECTORY(lib)
然后,cd lib ; touch CMakeLists.txt ; gedit CmakeLists.txt 内容如下:
SET(LIBHELLO_SRC hello.c)
ADD_LIBRARY(hello SHARED ${LIBHELLO_SRC})
然后进入build文件夹,进行编译 cmake … make
接下来进行共享库的安装和头文件安装:
在lib/CMakeLists.txt文件中添加如下指令:
INSTALL(TARGETS hello LIBRARY DESTINATION lib)
之后进行库的安装:
cmake -DCMAKE_INSTALL_PREFIX=
make
make intsall
接下来为使用外部共享库和头文件
在useHello.c所在目录,创建CMakeLists.txt文件,并编辑:
PROJECT(USEHELLO)
#头文件的搜索部分
INCLUDE_DIRECTORIES(/usr/include/hello)
ADD_EXECUTABLE(usehello useHello.c)
TARGET_LINK_LIBRARIES(useHello hello)
编译之后即完成
或者采用环境变量的方法进行外部库的链接使用:
export CMAKE_INCLUDE_PATH= 此命令在bash命令终端使用
然后在CMakeLists.txt文件中加入如下内容:
FIND_PATH(myheader hello.h)
IF(myheader)
INCLUDE_DIRECTORIES(${myheader})
ENDIF(myheader)
- 理解ORB-SLAM2框架

(a)ORB-SLAM2 将编译出什么结果?有⼏个库⽂件和可执⾏⽂件?
答:编译结果:输出多个可执行文件程序和多个库文件。
库文件:通过/src文件夹中的.cc文件生成动态库文件ORB_SLAM2
可执行文件:rgbd_tum、stereo_kitti、stereo_euroc、mono_tum、mono_kitti、mono_euroc
(b)ORB-SLAM2 中的 include, src, Examples 三个⽂件夹中都含有什么内容?
答:include文件夹包含:对应src中程序的代码函数头文件
src文件夹包含:相应程序的代码函数的c++文件
Examples文件夹包含:对应不同类别的相机的主程序(具体内容没仔细看,学完再回来补)。
(c)ORB-SLAM2 中的可执⾏⽂件链接到了哪些库?它们的名字是什么?
答:链接到以下库:
(1)OPENCV_LIBS
(2)EIGEN3_LIBS
(3)Pangolin_LIBRARIES
(4)/ORB-SLAM2/Thirdparty/DBoW2/lib/libDBoW2.so
(5)/ORB-SLAM2/Thirdparty/g2o/lib/libg2o.so
4.ORB-SLAM2的运行测试

1.如何将 myslam.cpp或 myvideo.cpp 加⼊到 ORB-SLAM2 ⼯程中?请给出你的 CMakeLists.txt 修改⽅案。
答:两种解决方案,如下所示
(1)如果要编译myvideo.cpp,在原有的CMakeLists.txt文件最后添加
add_executable(myvideo Examples/Monocular/myvideo.cpp)//这里生产的可执行程序在Examples/Monocular/里面
target_link_libraries(myvideo ${PROJECT_NAME})
根据myvideo.cpp的程序可知,可执行文件myvideo需要myslam.yaml、myvideo.mp4、ORBvoc.txt文件。因此修改myvideo.cpp程序,并将需要的文件复制到可执行myvideo所在的文件夹里。
// 参数文件与字典文件
// 如果你系统上的路径不同,请修改它
string parameterFile = "./myvideo.yaml";
string vocFile = "./ORBvoc.txt";
// 视频文件
string videoFile = "./myvideo.mp4";
(2)如果要编译myslam.cpp,同理上个步骤,不多说啦。
- 第二节课习题

(1)非齐次线性方程在A的秩与[A|B]的秩相同时方程有解,当R(A)=R(A,B)=n时方程有唯一解。
或者A为方阵且A阵可逆时,x有解且唯一
(2)高斯消去法原理
(3)QR分解:
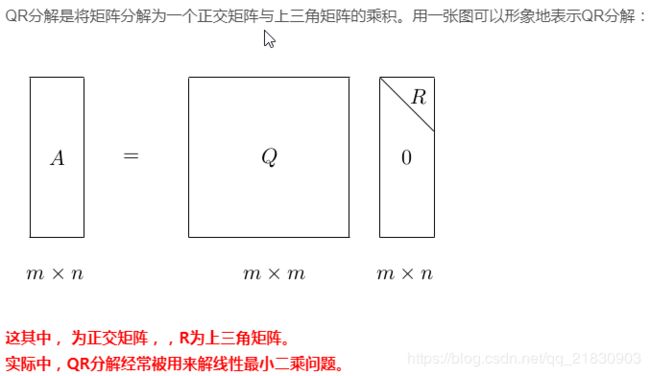
:百度文库的讲解PPT

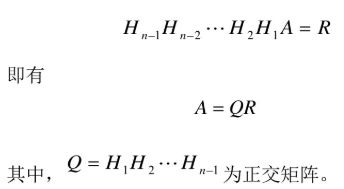
(4)cholesky分解原理:
注意:这里被分解的矩阵A必须是对称正定阵,L为下三角矩阵。 cholesky分解讲解
(5)编程实现:
#include
#include
#include
#include
#include
#define MATRIX_SIZE 100
using namespace std;
int main(int argc,char** argv)
{
Eigen::Matrix matrix_100;
matrix_100=Eigen::Matrix::Random();
cout< vnd,x;
vnd=Eigen::MatrixXd::Random(MATRIX_SIZE,1);
//QR分解结果
x=matrix_100.colPivHouseholderQr().solve(vnd);
cout<<"QR result"< #include
#include
#include
#include
using namespace std;
using namespace Eigen;
int main(int arcg,char** argv)
{
Quaterniond q1 = Quaterniond(0.55,0.3,0.2,0.2).normalized(); //定义并归一化四元数
Quaterniond q2 = Quaterniond(-0.1,0.3,-0.7,0.2).normalized();
Vector3d t1 ,t2,p1,p,p2;
t1 << 0.7,1.1,0.2;
t2 << -0.1,0.4,0.8;
p1 << 0.5,-0.1,0.2;
Isometry3d T_cw1 = Isometry3d::Identity();
T_cw1.rotate ( q1 );
T_cw1.pretranslate ( t1 );
Isometry3d T_cw2 = Isometry3d::Identity();
T_cw2.rotate ( q2 );
T_cw2.pretranslate ( t2 );
p = T_cw1.inverse() *p1; //不能用转置,因为这里不是纯旋转,见书42页
p2 = T_cw2 *p ;
cout<<"p2 = "< cmakelists文件:
cmake_minimum_required( VERSION 2.8 )
project( geometry )
# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )
add_executable( eigenGeometry eigenGeometry.cpp )
参考博客:
https://blog.csdn.net/weixin_41074793/article/details/84241776


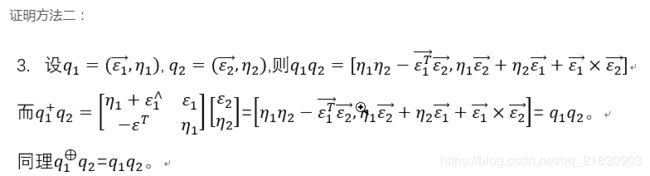
5.罗德里格斯公式的证明;
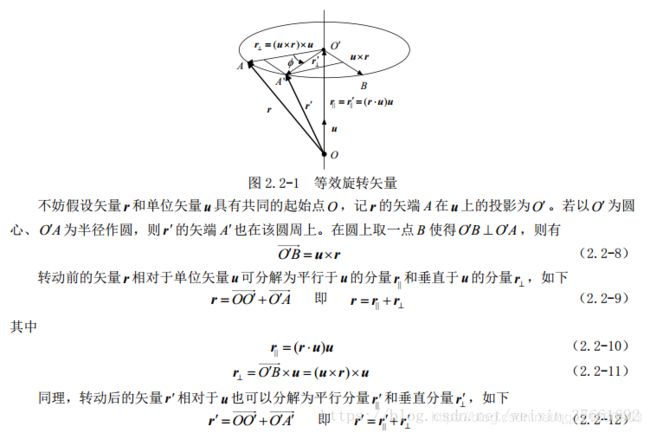





*第三讲习题

答:
群的定义:群是一种集合加上一种运算的代数结构
(1)整数集为{-2,-1,0,1,2}等,其满足群的封闭性、结合律、幺元,但是其不满足可逆性,整数的逆不再属于整数集,故{Z,+}不属于群
(2)自然数集为非负的整数集,如{0,1,2,3…},其满足群的封闭性、结合律、幺元,但是不满足可逆性,故{N,+}不属于群。
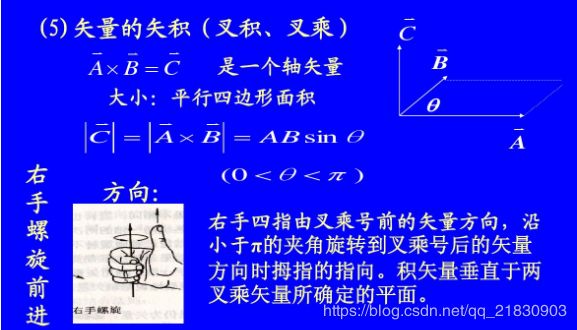
首先对于封闭性,axb仍为一个3x1的向量,满足封闭性
双线性:以x,y,z分别为三个相互垂直的坐标轴为例,可以发现计算结果满足该条性质,




cmake_minimum_required(VERSION 3.0)
project(draw_trajectory)
set(CMAKE_CXX_STANDARD 11)
#include_directories("/usr/include/eigen3")
find_package(Pangolin)
include_directories(${Pangolin_INCLUDE_DIRS})
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
add_executable(draw_trajectory draw_trajectory.cpp)
target_link_libraries(draw_trajectory ${Pangolin_LIBRARIES} ${Sophus_LIBRARIES})
添加的代码段:
ifstream file(trajectory_file);
if (!file)
{
cout << "Open file failure." << endl;
return 1;
}
for (int i = 0; i<620; i++)
{
double data[8] = { 0 };
for (auto& d : data)
file >> d;
Eigen::Quaterniond q( data[4], data[5], data[6],data[7]);
Eigen::Vector3d t(data[1], data[2], data[3]);
Sophus::SE3 SE3_traj(q, t);
poses.push_back(SE3_traj);
}
*第四节课习题

在对应cpp中增添代码段如下:
首先添加头文件 #include
double x=(u-cx)/fx;
double y=(v-cy)/fy;
double r=sqrt(pow(x,2)+pow(y,2));
u_distorted=x*(1+k1*pow(r,2)+k2*pow(r,4))+2*p1*x*y+p2*(pow(r,2)+2*x*x);
v_distorted=y*(1+k1*r*r+k2*pow(r,4))+p1*(r*r+2*y*y)+2*p2*x*y;
u_distorted=u_distorted*fx+cx;
v_distorted=v_distorted*fy+cy;
注意需要先将当前图像的像素坐标通过内参进行转换

注意本题在计算距离z时,没有给出焦距,再次自行设定为4cm。
for (int v = 0; v < left.rows; v++)
for (int u = 0; u < left.cols; u++) {
Vector4d point(0, 0, 0, left.at(v, u) / 255.0); // 前三维为xyz,第四维为颜色
// start your code here (~6 lines)
unsigned int d=disparity.at(v,u);
if(d==0)
continue;
cout< CMakeLists.txt:
cmake_minimum_required(VERSION 2.8.3)
project(disparity)
set(CMAKE_CXX_STANDARD 11)
find_package(OpenCV)
find_package(Eigen3)
find_package(Pangolin)
include_directories(${Pangolin_INCLUDE_DIRS})
#include_directories( "/usr/include/eigen3" )
include_directories(${EIGEN3_INCLUDE_DIR})
add_executable(disparity disparity.cpp)
target_link_libraries(disparity ${OpenCV_LIBS} ${Pangolin_LIBRARIES})

参考: 搜索矩阵对矩阵的求导
https://blog.csdn.net/daaikuaichuan/article/details/80620518
https://blog.csdn.net/GoodShot/article/details/79177606
(1)将AX对X的每一个分量求偏导,构成一个超向量。注意该向量的每一个元素都是一个矩阵。
此处:
矩阵Y对标量x求导:
相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M
Y = [y(ij)] --> dY/dx = [dy(ji)/dx]
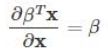
(2)
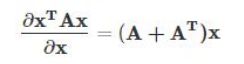
(3)
cmake_minimum_required( VERSION 2.8 )
project(practice)
find_package(Eigen3)
find_package(OpenCV)
include_directories(${EIGEN3_INCLUDE_DIR})
add_executable(prac gaussnewton.cpp)
target_link_libraries(prac ${OpenCV_LIBS})
代码部分:
注意此程序中雅克比矩阵表示为31,实际计算中应为13,程序中与此相反,与计算机的表示有关,H矩阵为3*3
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T J in Gauss-Newton
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
// start your code here
double error = 0; // 第i个数据点的计算误差
//error = 0; // 填写计算error的表达式
error=yi - (exp(ae * xi * xi + be * xi + ce));
Vector3d J; // 雅可比矩阵
//J[0] = 0; // de/da
//J[1] = 0; // de/db
// J[2] = 0; // de/dc
J[0]=-xi*xi*exp(ae * xi * xi + be * xi + ce);
J[1]=-xi*exp(ae * xi * xi + be * xi + ce);
J[2]=-exp(ae * xi * xi + be * xi + ce);
cout<<"jjjjjjjjj "<- 第五讲 视觉里程计
Oriented FAST 实际上为FAST特征再加上一个旋转向量